编程语言实现模式

很久之前已经把这本书看过一遍了，但是一直没有实践过!于是，拿出来再复习一遍，顺便记录笔记。关于这本书有几点：

1. ANTLR贯穿全书：作者是Terence Parr，这点也就不奇怪了
2. ANTLR生成的代码是LL(K)的
3. 偏重实践，原理很少，想看原理要去看龙书

另外，你应该先知道编译的过程大概分成哪几步骤以及为什么这样划分！废话少说，来看这本书的内容。

解析输入

词法分析和语法分析很多地方都是相同的，解析器结构如下：

public class G extends Parser {
    // 类型定义
    // 合适的构造函数
    // 规则对应的方法
}

在一个规则中包含很多子规则时，根据向前看符号来决定使用哪个，这个逻辑的代码描述可以用if-else来做：

if(向前看到alt1){
    // 匹配alt1
} else if(向前看到alt2){
    // 匹配alt1
}....

当然这里也可以用switch做，在规则上定义的一些常见操作有：

1. (T)?：T可有可无
2. (T)+：多个T
3. (T)*：零个或多个T

这些操作的代码描述：

// (T)?
if(向前看到T){ match(T);}
// (T)+
do{
    match(T);
} while(向前看到T)
// (T)*
while(向前看到T){
    match(T);
}

能利用好这三个操作大部分的规则都可以搞定了！词法分析相对语法分析了来说简单很多，Lexer会提供nextToken()来供Parser使用来不断地获取TOKEN：

public Token nextToken(){
    while(lookahead-char != EOF) {
        switch(lookahead-char){
            case 空白字符: { consume(); continue; }
            case 字符后面可能是T1: return T1();
            case 字符后面可能是T2: return T2();
			// ...
            default:
                出错;
        }
    }
    return EOF;
}

直观上来看用switch进行预测，相当于构造了一个状态机吧，其中consume()方法自增下标并将下一个字符当做向前看字符（消费字符）。在仅使用一个向前看符来进行语法分析时，也就是LL(1)，对于下面语法：

list : '[' elements ']';
elements : element (',' element)*;
element : NAME | list;

生成的Paser如下：

public class ListParser extends Parser {
    public void list(){
        match(ListLexer.LBRACK); // 匹配并消耗词法单元
        elements();
        match(ListLexer.RBRACK);
    }
    public void elements(){
        element();
        while(lookahead.type == ListLexer.COMMA) {
            match(ListLexer.COMMA);
            element();
        }
    }
    public void element(){
        if(lookahead.type == ListLexer.NAME) match(ListLexer.NAME);
        else if(lookahead.type == ListLexer.LBRACK) list();
        else throw new Error("语法错误");
    }
}

很简单的语法用LL(1)是没有问题的，对于稍微复杂一点的其预测能力差就暴露出来了，怎么办？当然是多拿几个进行预测！可以构造环形缓冲区来存放用来预测的TOKEN，另外增加两个方法：

1. LA：返回第k个向前看词法单元的类型
2. LT：返回第k个词法单元

那么文法：

element : NAME '=' NAME : NAME : list ;

对应的程序描述就变为：

public void element(){
    if(LA(1) == LookaheadLexer.NAME && LA(2) == LookaheadLexer.EQUALS) {
        match(LookaheadLexer.NAME);
        match(LookaheadLexer.EQUALS);
        match(LookaheadLexer.NAME);
    } else if(LA(1) == LookaheadLexer.NAME) {
        match(LookaheadLexer.NAME);
    } else if(LA(1) == LookaheadLexer.LBACK) {
        list();
    } else {
        throw new Error("语法错误!");
    }
}

但是LL(K)也不是万能的，如果向前看k个解决不了问题，那么向前无限个总应该可以搞定了吧？回溯解析中使用递归尝试不同的规则，在发现无法匹配时把消费掉的TOKEN吐出来：

public void rule() {
    if(speculate_alt1()){
        // 匹配alt1
    } else if(speculate_alt2()){
        // 匹配alt2
    } else { throw new Error("语法错误！"); }
}
public boolean speculate_alt1() {
    boolean success = true;
    mark();// 标记当前位置，供release使用
    try{
        // 匹配alt1
    } catch(Exception e){ success = false; }
    release();// 将消费掉的TOKEN重新放回去
    return success;
}

回溯解析最大的缺陷就是性能低，而其中一个原因则是做了不少重复工作，对于语法：

s : expr ':' | expr ';';

在尝试第一个子规则失败时会去尝试第二个，那么expr就会被匹配两次！如果能把之前匹配过的结果记住就好了（参考记忆化搜索），此时仅需要做一些很小的修改：

// 每个规则有一个Map来保存结果
Map<Integer, Integer> list_memo = new HashMap<Integer, Integer>;
public void list(){
    boolean failed = false;
    int startTokenIndex = index();
    if(isSpeculating() && aleadyParsedRule(list_memo)) return;
	try{_list();}
    catch(Exception e) {failed = true; throw e; }
    finally{
         if(isSpeculating())
             memoize(list_memo, startTokenIndex, failed);
    }
}
public void _list(){
    match(XXX);
    elements();
    match(XXX);
}

简单说明下上面用到的几个方法：

1. aleadyParsedRule：使用缓存的结果：成功返回TRUE、失败抛异常、未处理过返回FALSE
2. memoize：回溯时将结果记录到缓存

另外需要清楚一个细节：

推演时没有通过的try-catch逻辑在非推演时更不可能走到！

最后，在遇到上下文相关的语法时使用谓词是个不错的选择，用代码描述就是增加条件：

public void rule(){
    if(向前看符号测试alt1 && 谓词1) {
        // 匹配alt1
    } else if(向前看符号测试alt2 && 谓词2) {
        // 匹配alt2
    } ...
}
while(对循环的alt进行向前看符号判断 && 谓词判断) {
    子规则的代码用来匹配alt
}

到这里解析输入的逻辑基本上就看完了，简单来说：

1. Lexer产出Token流
2. Parser产出方法执行流

接下来我们就需要在Parser产出的方法执行流上面来进行分析。

分析输入

将源码结构化时一般用到两种方式：语法分析树和抽象语法树，从三个方面来看：

1. 紧凑：不含无用节点
2. 易用：很容易遍历
3. 显意：突出操作符、操作对象，以及它们互相间的关系，不再拘泥于文法

抽象语法树都要更优秀一些！程序实现时，我们在Parser匹配的过程中向方法中插入一些代码即可得到想要的树形结构：

public void rule(){
    RuleNode r = new RuleNode("规则名");
    if(root == null) root = r;
    else currentNode.addChild(r);
    ParseTree _save = currentNode;
    // 原始的规则代码
    currentNode = _save;
}

要比想象的简单很多，因为在LL的解析中：

解析过程就可以看做是在语法分析树上做DFS，任意当前树节点的父亲必然是前面遍历过的某个节点！

不同实现节点的方式后续树的遍历等都是有影响的，有如下方式：

类型	含义
同型AST	只有一种节点类型AST，要依据TOKEN来区分不同类型
规范异型AST	从基类AST派生不同的节点类型，子节点列表统一
不规范异型AST	可以添加不同的子节点属性，能够让代码的可读性更高

好不容易拿到树形结构了，遍历它也不是一个轻松的活。回想大学用Java写二叉树遍历的时候通常是这样：

public class Node {
    Node left, right;
    void visit(){
        left.visit();
        right.visit();
    }
}

把遍历操作嵌入节点内部最明显的缺点是：逻辑散落在各节点中操作起来很麻烦，可以将遍历操作统一放到一个地方：

public abstract class VecMathNode extends HeteroAST {
    public abstract void visit(VecMathVisitor visitor);
}
public interface VecMathVisitor {
    void visit(AssignNode n);
    void visit(PrintNode n);
    void visit(StatListNode n);
    void visit(VarNode n);
    // ...
}

在实现的时候在Visitor中将this传递就可以达到遍历的目的了：

public class PrintVisitor implements VecMathVisitor {
    public void visit(AssignNode n){
        n.id.visit(this);// 看这里
        System.out.print("=");
        n.value.visit(this);
    }
}

提到外面代码量并没有减少，但是这种代码很有规律，ANTLR可以大幅度地减少你的工作量！当然还有其他的方式来实现相同的目的，这里就不啰嗦了。

遍历语法树的过程中要和两个东西打交道：

1. 操作
2. 符号

操作很简单，把子节点收集起来进行计算、处理就行了，但是符号就没那么随意，关键就是作用域：

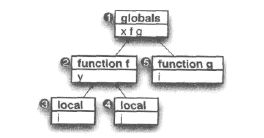
// 1
int x;
void f(){ // 2
    int y;
    { int i; } // 3
    { int j; } // 4
}
void g(){ // 5
    int i;
}

嵌套的作用域更加容易理解，嵌套关系可以用树形结构来表示（这种作用域的特点是只有一个父节点），上面这段代码生成的作用域如下：

在遍历树的时候用一个栈来保存能访问到的作用域：

在这个过程中用到的操作有：

操作	作用
push	向栈中压入作用域
pop	作用域结束后，要将当前的作用域弹出栈
def	在当前作用域中定义符号
resolve	解析符号

面向过程的变成语言很简单，这些已经够了，但是在面向对象编程的时候就不行了：

// 1 全局
class A {// 2
public :
    int x;
    void foo()// 3
    { ; } // 4
}
class B : public A {// 5
    int y;
    void foo()// 6
    {// 7
        int z =  x + y;
    }
}

由于继承关系的存在，在查找符号的时候不仅是要在当前类中找，而且要去父类中找，也就是说此时的父节点就不止一个了：

对于像a.x = 3这种访问对象属性的行为就不能按照上面套路来了，需要增加一个操作：

操作	作用
resolveMemeber	解析成员，只会根据superClass递归查找

到这里还没完，Java中的Class的定义可以在使用之前，那么在上面的处理属性引用时发现还没定义！直观的解决方法：

预先遍历一次来定义类型。

这里要小心处理好符号和作用域的关系。有了作用域和符号表之后需要对其进行简单的分析：

操作	含义
计算表达式类型	操作的返回结果
自动类型提升	根据操作的对象来决定是否需要对其中低等级的进行提升
静态类型检查	操作的对象类型是否合法
多态类型检查	面向对象中的父子关系

简单来说都是在遍历AST的时候完成的，下面来看如何运行程序~~

解释执行

经过上面这些步骤我们已经知道了源码所要表达的意思，那么就可以用代码来实现其逻辑（也就是解释执行），根据实现方式区分有：

1. 语法制导解释器：不会生成AST，在解析源码的过程中完成；
2. 基于树的解释器：先构建AST，在遍历的过程中完成执行；

这两种方式很好理解，用1+2*3的例子玩一玩就可以了，感觉这部分讲的有点啰嗦。用上面的方式执行优点简单、粗暴，缺点是耦合太强了，为了化解便有了：

1. 字节码汇编器：将便于阅读的汇编语言翻译为二进制形式的字节码指令；
2. 栈式解释器：执行指令时使用操作数栈存放临时变量；
3. 寄存器解释器：执行指令时使用虚拟寄存器存放参数、局部变量和临时变量；

用中间指令（也可以理解为原子API）作为过渡，这样以后再有其他的DSL来了，只需要将其翻译为这种中间指令就可以了。

生成输出

要让自己定义的DSL可执行最简单的办法就是将其翻译为现有的一种语言，和各种CC干的差不多：

比如ANTLR就是讲文法翻译为Java代码。

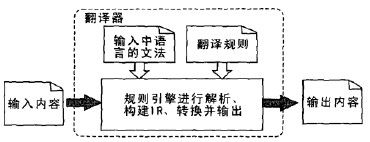
语法制导是最简单的方案，读入内容在解析的过程中完成输出，无法处理前向引用：

而基于规则则是专注于指定一条一条的规则，在匹配到某条规则的时候执行（输出）对应的操作：

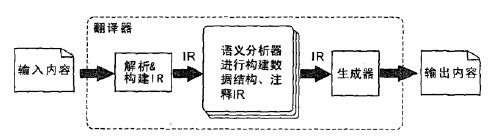
工业界普遍流行的是模型驱动翻译，先创建AST，然后在遍历的过程中生成代码：

对于简单的DSL可以使用模板（比如Velocity）来简化输出，但是难点并不在这里。

总结

这本书对于想实现DSL的人来说还是挺有作用的：例子、代码实现，但是想要学习理论的恐怕要失望了，因为这里几乎是没有的。

看到网上有人评价这本书能超过龙书，不知道是从哪里看出来的，类型差别这么大如何比较的？

转载:编程语言实现模式