USACO Training Section 1.2 Transformations 解题报告&AC代码
解题报告:
这道题乍一看觉得挺难,但是看到它说只会进行一次变换的时候…可以松口气了。那么接下来的工作变得轻松而…不怎么愉快…
分别将7种变换(当然6、7是打酱油的)实现后,在比较一次就好啦,简单高效。
下面来代码。
AC代码:
/*
ID: yuanmz91
PROG: transform
LANG: C++
*/
#include <fstream>
#include <iostream>
#include <memory.h>
using namespace std;
const int MAX_SIZE = 11;
bool change(char [MAX_SIZE][MAX_SIZE], char [MAX_SIZE][MAX_SIZE], int, int);
int main()
{
ifstream fin("transform.in");
ofstream fout("transform.out");
int size;
char square[MAX_SIZE][MAX_SIZE], target[MAX_SIZE][MAX_SIZE];
fin >> size;
for(int i = 0; i != size; ++i)
{
fin >> square[i];
}
for(int i = 0; i != size; ++i)
{
fin >> target[i];
}
for(int i = 0; i != 7; ++i)
{
if(change(square, target, size, i))
{
fout << i + 1 << endl;
break;
}
}
return 0;
}
bool change(char x[MAX_SIZE][MAX_SIZE], char y[MAX_SIZE][MAX_SIZE], int len, int mode)
{
char tmp[MAX_SIZE][MAX_SIZE];
for(int i = 0; i != len; ++i)
{
for(int j = 0; j != len; ++j)
{
switch(mode)
{
case 0:
tmp[i][j] = x[len - j - 1][i];
break;
case 1:
tmp[i][j] = x[len - i - 1][len - j - 1];
break;
case 2:
tmp[i][j] = x[j][len - i - 1];
break;
case 3:
tmp[i][j] = x[i][len - j - 1];
break;
case 4:
tmp[i][j] = x[i][len - j - 1];
for(int k = 0; k != 3; ++k)
{
if(change(tmp, y, len, k))
{
return true;
}
}
return false;
break;
case 5:
tmp[i][j] = x[i][j];
break;
case 6:
return true;
}
}
tmp[i][len] = 0;
}
for(int i = 0; i != len; ++i)
{
for(int j = 0; j != len; ++j)
{
if(tmp[i][j] != y[i][j])
{
return false;
}
}
}
return true;
}
国际惯例,题目在这里……
英文版:
中文版:
描述
一块N x N(1<=N<=10)正方形的黑白瓦片的图案要被转换成新的正方形图案。写一个程序来找出将原始图案按照以下列转换方法转换成新图案的最小方式:
1:转90度:图案按顺时针转90度。
2:转180度:图案按顺时针转180度。
3:转270度:图案按顺时针转270度。
4:反射:图案在水平方向翻转(以中央铅垂线为中心形成原图案的镜像)。
5:组合:图案在水平方向翻转,然后再按照1到3之间的一种再次转换。
6:不改变:原图案不改变。
7:无效转换:无法用以上方法得到新图案。
如果有多种可用的转换方法,请选择序号最小的那个。
只使用1--7中的一个步骤来完成这次转换。
格式
PROGRAM NAME: transform
INPUT FORMAT:
file (transform.in)
第一行: 单独的一个整数N。
第二行到第N+1行: N行每行N个字符(不是“@”就是“-”);这是转换前的正方形。
第N+2行到第2*N+1行: N行每行N个字符(不是“@”就是“-”);这是转换后的正方形。
OUTPUT FORMAT:
file (transform.out)
单独的一行包括1到7之间的一个数字(在上文已描述)表明需要将转换前的正方形变为转换后的正方形的转换方法。
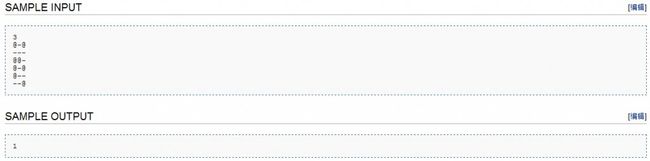
哦……这里还有测试数据~~
Here are the test data inputs: ------- test 1 ---- 3 --- --- --- --- -@- --- ------- test 2 ---- 5 -@@@- -@@-- -@--- ----- ----- ----- ----@ ---@@ --@@@ ----- ------- test 3 ---- 5 @@@@@ @---@ @@@@@ @@@@@ @@@@@ @@@@@ @@@@@ @@@@@ @---@ @@@@@ ------- test 4 ---- 6 -@-@-@ @-@-@- -@-@-@ @-@-@- -@-@-@ @-@-@- @-@-@- -@-@-@ @-@-@- -@-@-@ @-@-@- -@-@-@ ------- test 5 ---- 3 @@@ --- @@@ @@@ --- @@@ ------- test 6 ---- 4 @@@@ @@@@ -@@@ @@@@ @@@@ @@@@ @@@- @@@@ ------- test 7 ---- 4 @-@@ @@@@ @@@@ @@@@ @@@@ @@@@ @@@@ @-@@ ------- test 8 ---- 10 @--------@ ---------- ---------- ---------- ---------- ---------- ---------- ---------- ---------- ---------- @--------- ---------- ---------- ---------- ---------- ---------- ---------- ---------- ---------- ---------@