机器学习基本算法通俗总结

机器学习基本算法通俗总结

本文章参考内容
1斯坦福大学Andrew Ng大帝的机器学习早期教程及其在coursera上的视频
2Peter Harrington 的机器学习实战
3李航老师的统计学习方法等
4本人水平有限还望网友多指教。

目录

课程的选择

对于这两个视频（链接在前面）如何选择的问题，第一个是很久之前的视频，在网易公开课就有，其中内容丰富，讲的东西比新的coursera上的多，而且数学推导也很多，但是对于想快速入门的童鞋还是选择新的比较好，因为比较容易。新的视频已经有网友翻译了，我这有一份，其中有一个是中国海洋大学博士生黄海广童鞋的作品，需要翻译字幕的同学可以给我发邮件。另外台湾国立大学的林轩田老师的课程我这也有，需要的也可以言语一声。还有类似课程的选择，请参见这篇文章，相关书籍请看这篇文章，各种主页请看这篇文章，其他资源看这里。另外备受推崇的UFLDL教程,请戳这里。暂时到这里，以后有资源慢慢加上，先开始总结吧。

1线性回归Linear Regression

1.1线性回归Linear Regression

首先啥是回归呢，回归分析（regression analysis）就是找一下自变量与因变量（写自变量与因变量主要是为了好理解，不严谨的噢）的关系，线性回归呢就是找一个一次方的关系来拟合真正的因变量，如下式：

hθ=θ0+θ1X1+θ2X2

其中 θi 叫做参数（parameters）也可以叫权重（weight），而我们的回归分析的大部分时间就是为了找这个参数，这些参数时怎么来的呢，通俗的说就是根据已有的样本（包含自变量Xi与因变量Y）找规律找的，具体来说就是先搞一个方程，这些参数都满足这个方程（cost function），然后用解方程的方法来解这些参数。这种根据已有样本中有因变量（姑且就这么叫吧，毕竟初中就开始有这个词了）的分析学习方法，就叫做 监督学习Supervised Learning，相反如果样本中 没有因变量，我们没法去列一个方程，就给他一些提示，比如去把距离比较近的样本聚在一起，让电脑自己去计算，这类算法就叫做 无监督学习Unsupervised Learning。

从上面可以看到，线性回归解参数很重要，而解参数所需要的方程就是解除参数的重要前提了。这个方程又叫做cost function,线性回归的时候我们的方程如下

J(θ)=1/2∑i=1m(h(θ)(x(i))−y(i))2

其中 h(θ) 就是上面提到过的， y(i) 就是已知的因变量，整个方程就是想让 J(θ) 等于零，整个方程的意思就是寻找参数 θ 让我们之前的方程 h(θ) 与已知的因变量 y(i) 相同，然后我们就可以利用这个 h(θ) ，输入一个新的自变量，就可以求出新的因变量了。这就是 预测。
另外，为什么要用这个方程呢，其实是可以证明的，其中可以用 最大似然法在 概率学上证明，此处就不做详解了。另外为了防止过拟合，还会让方程正则化，想看的同志们 请戳这里。

好，我们现在已经有了方程，那么如何解这个方程呢，上面的cost function 的目标是让 J(θ) 尽量的减小，再看一下公式：

J(θ)=1/2∑i=1m(h(θ)(x(i))−y(i))2

当 θ 取值不同时， h(θ) 是不同的，y是已知的因变量，所以 J(θ) 也就随着 θ 变化，那如何使得 J(θ) 最小呢，看下图：
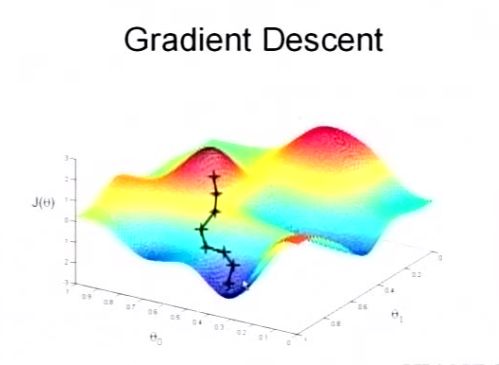
让 θ 沿着 J(θ) 的导数为负的方向走就可以啦。这种解决的方法叫做 梯度下降法gradient descent。
当然这方法完整的步骤写出来还是很长的，但是在网易公开课视频上Ng已经做了比较详细的推到了，有兴趣的可以看一下。
另外，这种方法又分为batch gradient descent 、minibatch gradient descent和stochastic gradient descent。
除了梯度下降法，解决这个问题还有很多别的方法，视频中还介绍了使用线代知识的 正规方程法。

1.2局部加权线性回归Locally Weight Linear Regression

上面的线性规划都是线性的，很多非线性的回归分析是不能很好的利用这个方法的。比如下图（图片是盗的~）：

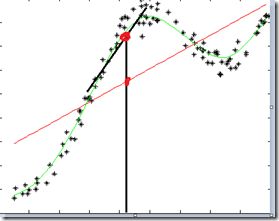
如果我们想预测x=0时（就当中间的黑线处x=0）的y值，如果直接用线性回归显然是不行的，这里想了个办法，就是预测x=0时，只考虑x=0局部附近的值，就用局部几个值来拟合线性回归方程，这时候就会得到黑色斜线啦，是不是效果还可以。你们人类真聪明。
可能有同学会问，这局部的几个点是怎么选的呢，聪明的人类是用了全部的点，只不过把目标周围的点的权重弄大，把远方的点的权重弄得接近于零，这就是局部加权线性回归的来历。要注意的是，这个加权的方法是套用了一个和高斯方程长得很像的方程。
我们可以发现，局部加权线性回归的参数是随着拟合点的不同而变的，这类方法叫做非参数学习方法，普通的线性回归的参数时定值，所以叫做参数学习方法。

2分类与逻辑回归Logistic Regression

前面讲的是线性回归相当于拟合一个连续函数，这里的分类相当于分出一个离散的函数。
在线性回归中我们要拟合的函数为（其实他的名字叫Hypotheses）

hθ=θ0+θ1X1+θ2X2

在这个Logistic Regression中我们的Hypotheses是

hθ=11+e−θTx

它的图像是

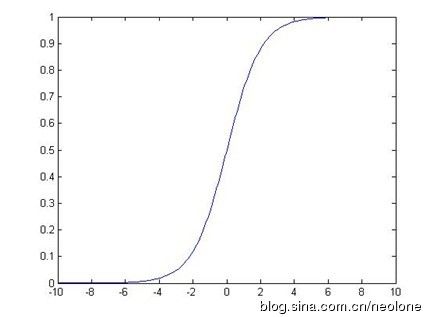
这样可以看出如果 θTx 小于零，那么h接近于0，相反就接近于1，这样就实现了分类。我们要做的事情还是找出参数，使得这个hypotheses最接近于实际。我们假设：

P(y|x;θ)=(hθ(x))y(1−hθ(x))1−y

这样就有以下关系

P(y=1|x;θ)=hθ(x)

P(y=0|x;θ)=1−hθ(x)

根据最大似然法将所有的P乘在一起就得到了在参数 θ 下的似然方程

L(θ)=P(y⃗ |x;θ)

最后既可求在L最大时候的 θ 。
求这个方程时可以使用前面使用过的 梯度下降法也可以使用 牛顿法，牛顿法迭代次数少，但是计算复杂，这里就不详细介绍了。
值得一提的是，这里的利用梯度下降法得到的迭代公式与线性回归的迭代公式是 一样的，好巧。另外视频中还提到了还有其他算法（perceptron learning algorithm）的迭代形式也是这样。

3广义线性模型 Generalized Linear Models GLM

前面已经讲了线性回归和logistic分类，其实他们俩都属于同一个组织—广义线性模型（GLM）。具体了解这个模型及exponential family可以戳这里和这里。
顺道说一下，这个模型也解释了logistic函数为啥长那样。

4生成学习模型 Gneerative Learning algorithms

先挖个坑，以后来补、

4.1 Gaussian discriminant analysis(GDA)

4.2 Naive Bayes

4.3 Event models

5 神经网络 Neural Network

6 支持向量机 Support vector machines

支持向量机由Cortes与Vapnik提出，Boser、Guyon和Vapnik又引入核技巧。本文将首先从线性可分的支持向量机说起。注意，本节介绍的不严谨，但是有助于理解，具体的KTT条件的等问题，可以另行参阅相关文档。

6.1 量化间隔

简单来说，线性可分时支持向量机就是寻找一个超平面，将可以区分的训练数据分开，我们要做的就是确定这个超平面的方程。

如上图，想要用一条直线将两个点分开就是这个的特殊情况，在二维图里 这个超平面就是条直线，三维图里就是个空间面，更高维就没法画出来了。这条直线怎么弄比较好呢，显然当这条线距离这两个点的距离越大越好。直线到点的距离公式是什么呢，以前我们是这样写的：

d=|Ax0+By0+C|A2+B2−−−−−−−√

现在我们洋气一点：
把原来的方程ax+by+c=0写成向量形式： w⋅x+b=0 ，此时 x 为向量包含x1,x2……,在高维时可以称呼这个方程为超平面的方程，但是他们的距离表达式还是相似的：

γi=w⋅xi+b||w||

这里||w||为w的范数，注意这里的 γi 没有加绝对值，还是有正负的。（其实这里应该引入几何间隔和函数间隔的概念~）
代入超平面的公式计算的距离 γi 为负值时，就说这边的点的标签都是-1，代入另一边的点位+时就说这边点的标签为+1，设这里的标签为 yi ,这样一来也就是根据y的值给分类了是不？
剩下的就是确定这个超平面的表达式了，有了表达式就可以代入分类了，表达的时的参数怎么来的呢？老样子，还是根据训练数据来计算的，在logistic中，我们的所用的w可以用梯度法来解，这里我们的的解法是smo，后面我们会详细介绍
现在，我们首先我们先来看如何利用训练数据
1. 得到超平面表达式的目标是：将离着超平面最近的点分开，而且要使点到平面的距离最大，这样是分离的最好的时候
2. 我们所说的距离其实就是 γiyi ，我们要做的就是使得任意i 代入后得到最小的距离的距离最大化,bang bang bang bang ~，我们的主角出来了其实我们就是想要 γi=w⋅xi+b||w|| 最大化
3. 为了理解方便，我们回到刚开始引入的Ax+By+C=0的例子，其实对于任意的x,y 如果将A,B,C同时扩大或者缩小，对于求距离时没有影响的，对于我们要找到的超平面也是没有影响的，这样ABC太自由，上面第二条的式子的最大化是有困难的，所以这里我们把ABC的自由度降低，将 w⋅xi+b 的值设置为1（其实可以设为任意一个非零的你喜欢的，这里的1可以理解为单位1），这样第二条中的 γi=w⋅xi+b||w|| 就可以分解为在 w⋅xi+b=1 的条件下求||w||的最小值。（跳过几何距离的概念讲这个似乎还要简单些噢，多年的老便秘也通了）
4. 上面说到使最小的为1，那么对于所有的数值来说就是任意的训练数值在都大于等于1

到此为止我们得到如下的式子：

min1/2||w||2(此处将||w||最小化与将||w||2最小化等价)s.t.yi(wxi+b)≥1

好，对于上面这种二次规划问题（quadratic program）我们可以用广义拉格朗日乘子法解
但是这里我们要用的 拉格朗日对偶lagrange duality来求
简单来说就是把这个问题转化为另外等价的问题来求这个二次规划问题

6.2 拉格朗日对偶lagrange duality

了解拉格朗日对偶问题之前，还是需要先了解下拉格朗日乘子法lagrange multipliter, 在我们学习高数时，求在边界上的极值就用了拉格朗日乘子，现在不同的地方在于多了一个不等式约束条件，但是依然可以写成下式：

L(w,b,α)=12||w||2−∑i=1mαi[yi(wxi+b)−1]

其中， yi(wxi+b)≥1 ，所以 α≥0 因为这样如果有不满足条件的w,b出现，那么后面的部分就是小于0的数，乘以一个大于零的alpha，得到的l就会因为减去一个负数而增加，就不会是最小值，上面的式子里有三个未知数，如何求呢：
我们先控制 α 使L变的最大，（如果你现在想到了我们的目标是求w的最小值，先不要急），这个时候不满足约束的particular value of w,b都会使得L变为 ∞ ,而满足的呢，因为要是使得L变的最大，那么 α 就会为0，也就是这时候满足的要求的L（w）依然为 12||w||2 ，然后我们在控制w,使L最小就可以了，可以写成下面的式子：

w,bminα:α≥0maxL(w,b,α)

而对偶问题的意思就是有一个下面的公式与上面的公式等价：

α:α≥0maxw,bminL(w,b,α)

通俗点说就是先对w,b求极小，然后对 α 求极大，得到的结果却与我们原来的问题相同（其实相同的原因是满足KTT条件），对偶问题有什么好处呢，慢慢听我说
首先我们对L求w和b的偏导，求最内部的 w,bminL(w,b,α) 因为式子里一共有三个未知数，可以得到两两之间的关系，然后用x,y, α 来代替w,b就得到了 w,bminL(w,b,α) ， 然后就maxL就变成了 α 的函数，求使得L最大的 α ，这时的边界也就是最大了。其中在L对w求偏导时可以得到

w=∑i=1nαiyixi

在求b的偏导时得到了

∑i=1nαiyi=0

b也可以由条件来由若干参数y,x,alpha计算

也就是说求得alpha就可以求得超平面的方程了！但是alpha如何计算呢，后面会将到smo算法
好了到此为止，基本的svm你已经懂了，虽然很多地方讲的不严格，但是还是比较容易理解的，更严密的推理请看我们开始时所写的参考的书籍及课程

6.3我们要求松一点：软间隔

上面全部都讲的是严格线性可分的条件，但是有些不是线性可分的情况，一条线压根就分不开怎么办，我们前面分开的时候用的要求是让间隔最大，这里我们为了让在能够分开大多数点的前提下要求松一点，也就是不要求间隔这么大，对原来的最小间隔 w⋅xi+b 可以小一些让他等于 1−ξi ,然后重复6.1 6.2，不同的是
这里的最开始的目标函数变为了

min1/2||w||2+C∑i=1nξis.t.yi(wxi+b)≥1−ξiξi≥0

在对L求导时 不仅要求W b 的偏导还要求 ξi 的偏导，同样代入之后得到的结果还是一个关于 α 的函数，我们要做的依然是在求 α ，不同的是在硬间隔的 α 需要满足的条件有

∑i=1nαiyi=0且αi≥0

这里在求偏导时得到的约束条件变为了

∑i=1nαiyi=0且C≥αi≥0

此时我们通过解 α 得到的超平面的w是唯一的但是b不是唯一的，我们可以取符合条件的样本点的平均值

若 ξi=0，αi<C ,此时的样本点正好落在边界上，就像原来的边界上的点
若 0<ξi<1，αi=C ,此时的样本点分类正确，但是离着原来的分割线（在多维空间叫超平面）的距离却很小
若 ξi=1，αi=C ,此时的样本点在超平面上
若 ξi>1，αi=C ,此时的样本点分类错误
补充一点：超平面的方程为：

wx+b=∑i=mαiyi<xi,x>+b

这是经过推导出来的，有兴趣的可以去看看相关证明哦

6.4其实我也可以是弯的：非线性问题、kernels核函数

上面我们看到的都是在线性时的分类，只要确定一个超平面，在平面一侧的就是一类，另外一侧就是另外一类，但是如果线性不可分的情况怎么办呢，如下图：

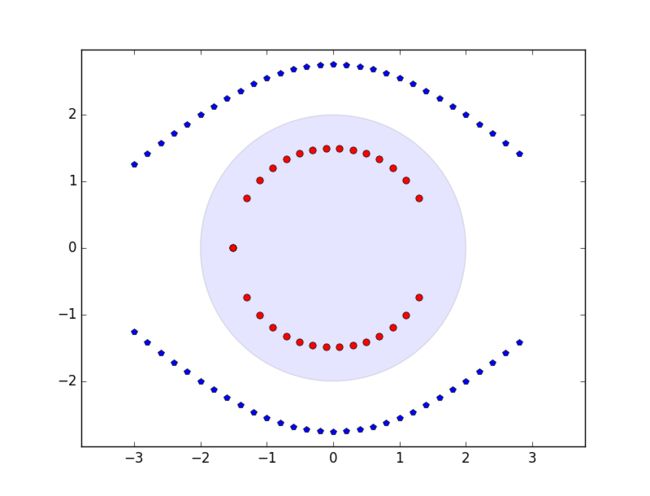
可以看出这个图可以用一个圆或者椭圆的形状来将它分类，圆的公式是ax^2+by^2+cx+dy+e=0
而我们用的svm里面的二维分类面的直线是ax1+bx2+c=0,
乍一看貌似不太容易利用，但是精彩的地方出来了，如果我们把x^2 y^ x y 分别用z1 z2 z3 z4代替，圆的表达式是不是就变成了下面的形状

az1+bz2+cz3+dz4+e=0

**是不是看起来很爽，把弯变成了直的
这就是利用增加维度的方法，把原来2维下的非线性问题转化为了4维下的**线性问题
理论上我们只要不挺的增加维度就可以把非线性问题转为线性问题，然后可以利用我们的svm了，只不过现在的超平面变为了：

wz+b=∑i=mαiyi<zi,z>+b

但是这样也带来了很多困难：z的维度比原来x的维度大的多的多，如果再来计算内积就需要很多很多的内存
怎么办呢
神奇的核函数出现了
核函数就是可以在计算 <zi,z> 不用先将x转化为z,再求z的内积，而是，而是，而是，而是，直接利用 K(xix)=<zi,z> ：可以这样理解：有一个函数， 输入原来的低维的x直接就可以计算出来高维的内积，你说神奇不神奇，你说神奇不神奇！o~神奇的kernel！！！！
而且有好几个函数都可以达到这个效果
好了现在有了核函数非线性也可以算了，就还剩下，求 α 了！！！

6.5 smo

还记得6.2我们用对偶问题将间隔最大的问题转化成了求 α 使“公式”最大的问题。这个关于 α 的公式当时没有推导，现在我们以意会为主
我们现在就开始求 α
首先要知道 α 有好多的，有多少个点就有多少个 α ，我们关于求 α 的式子大体形式如下：
求最大的式子=a α1 +b α2 +c α3 +……+d α1 α1 +e α1 α2 +f α1 α2 +g α1 α2 α3 ……(前面的系数的计算中中也有kernel的参与)而且这些 α 还有些约束，
1. 所有的 αiyi 之和为0，
2. 所有的 αi 大于等于0小于等于C（还记否？）
这么多的 α 一下也不好求哇~~~~
有个叫SMO的序列最小最优化算法，名字不重要，我们先讲讲思路：
1. 若水三千只取一瓢，我们先去两个 α ： α1 ， α2 ，其他的都选取随便的一个定值，因为有条件1限制，所以，当我们改变这两个中 一个时，另外一个也会跟着变的。这样我们就可以用 α1 来表示 α2 了，然后代入求最大的式子，就得到了只有 α1 的多项式
2. 求只有一个未知数的多项式的最大值总会吧，没错，求导导数为零的点就是最优解，但是这里还有前面的条件1、条件2来约束，根据这些条件我们可以求出 α1 的最大最小范围[L,H]，所以如果我们求出的 α1 不在范围内，就就近取一个在范围内的最优值。

7 聚类 Clustering

K-means

混合高斯

Jesen不等式

EM

8 推荐系统 Recommender systems

8.1 基于内容

8.2 协同过滤

8.3 矢量化推荐

9 异常检测

10 强化学习

11 其他

11.1 偏差分析

11.2 降维

……………………