数据结构与算法04 之二叉树

本文为博主原创文章，转载请注明出处： http://blog.csdn.net/eson_15/article/details/51138663   

        在有序数组中，可以快速找到特定的值，但是想在有序数组中插入一个新的数据项，就必须首先找出新数据项插入的位置，然后将比新数据项大的数据项向后移动一位，来给新的数据项腾出空间，删除同理，这样移动很费时。显而易见，如果要做很多的插入和删除操作和删除操作，就不该选用有序数组。

        另一方面，链表中可以快速添加和删除某个数据项，但是在链表中查找数据项可不容易，必须从头开始访问链表的每一个数据项，直到找到该数据项为止，这个过程很慢。

        树这种数据结构，既能像链表那样快速的插入和删除，又能想有序数组那样快速查找。这里主要实现一种特殊的树——二叉（搜索）树。二叉搜索树有如下特点：一个节点的左子节点的关键字值小于这个节点，右子节点的关键字值大于或等于这个节点。插入一个节点需要根据这个规则进行插入。

        删除节点时二叉搜索树中最复杂的操作，但是删除节点在很多树的应用中又非常重要，所以详细研究并总结下特点。删除节点要从查找要删的节点开始入手，首先找到节点，这个要删除的节点可能有三种情况需要考虑：

         ·该节点是叶节点，没有子节点

         ·该节点有一个子节点

         ·该节点有两个子节点

         第一种最简单，第二种也还是比较简单的，第三种就相当复杂了。下面分析这三种删除情况：

        要删除叶节点，只需要改变该节点的父节点对应子字段的值即可，由指向该节点改为null就可以了。垃圾回收器会自动回收叶节点，不需要自己手动删掉；当节点有一个子节点时，这个节点只有两个连接：连向父节点和连向它唯一的子节点。需要从这个序列中剪断这个节点，把它的子节点直接连到它的父节点上即可，这个过程要求改变父节点适当的引用（左子节点还是右子节点），指向要删除节点的子节点即可；第三种情况最复杂，如果要删除有两个子节点的节点，就不能只用它的一个子节点代替它，比如要删除节点25，如果用35取代它，那35的左子节点是15呢还是30？

   

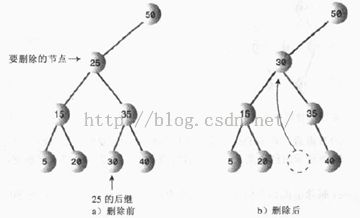
        因此需要考虑另一种方法，寻找它的中序后继来代替该节点。下图显示的就是要删除节点用它的后继代替它的情况，删除后还是有序的。（这里还有更麻烦的情况，即它的后继自己也有右子节点，下面再讨论。）

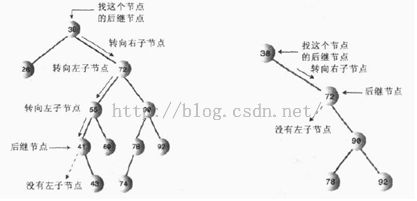
        那么如何找后继节点呢？首先得找到要删除的节点的右子节点，它的关键字值一定比待删除节点的大。然后转到待删除节点右子节点的左子节点那里（如果有的话），然后到这个左子节点的左子节点，以此类推，顺着左子节点的路径一直向下找，这个路径上的最后一个左子节点就是待删除节点的后继。如果待删除节点的右子节点没有左子节点，那么这个右子节点本身就是后继。寻找后继的示意图如下：

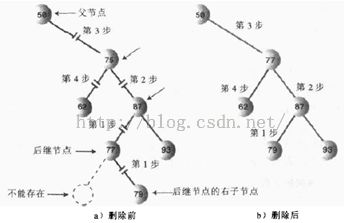
        找到了后继节点，现在开始删除了，先看第一种情况，后继节点是delNode右子节点的做后代，这种情况要执行以下四个步骤：

         ·把后继父节点的leftChild字段置为后继的右子节点；

         ·把后继的rightChild字段置为要删除节点的右子节点；

         ·把待删除节点从它父节点的leftChild或rightChild字段删除，把这个字段置为后继；

         ·把待删除的左子节点移除，将后继的leftChild字段置为待删除节点的左子节点。

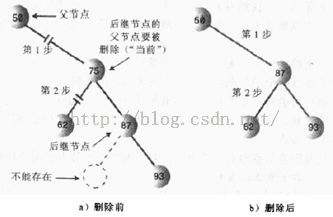
        如下图所示：

        如果后继节点就是待删除节点的右子节点，这种情况就简单了，因为只需要把后继为跟的子树移到删除的节点的位置即可。如下图所示：

        看到这里，就会发现删除时相当棘手的操作。实际上，因为它非常复杂，一些程序员都尝试着躲开它，他们在Node类中加了一个Boolean字段来标识该节点是否已经被删除，在其他操作之前会先判断这个节点是不是已经删除了，这样删除节点不会改变树的结构，。当然树中还保留着这种已经删除的节点，对存储造成浪费，但是如果没有那么多删除的话，这也不失为一个好方法。下面是二叉搜索树的主要代码：

public class BinaryTree {
	private BNode root; //根节点
	
	public BinaryTree() {
		root = null;
	}
	
	//二叉搜索树查找的时间复杂度为O(logN)
	public BNode find(int key) { //find node with given key
		BNode current = root;
		while(current.data != key) {
			if(key < current.key) {
				current = current.leftChild;
			}
			else {
				current = current.rightChild;
			}
			if(current == null) {
				return null;
			}
		}
		return current;
	}
	
	//插入节点
	public void insert(int key, double value) {
		BNode newNode = new BNode();
		newNode.key = key;
		newNode.data = value;
		if(root == null) { //if tree is null
			root = newNode;
		}
		else {
			BNode current = root;
			BNode parent;
			while(true) {
				parent = current;
				if(key < current.data) { //turn left
					current = current.leftChild;
					if(current == null) {
						parent.leftChild = newNode;
						newNode.parent = parent;
						return;
					}
				}
				else { //turn right
					current = current.rightChild;
					if(current == null) {
						parent.rightChild = newNode;
						newNode.parent = parent;
						return;
					}
				}
			}
		}
	}
	
	//遍历二叉树
	public void traverse(int traverseType) {
		switch(traverseType)
		{
		case 1: System.out.println("Preorder traversal:");
				preOrder(root);//前向遍历
				break;
		case 2: System.out.println("Inorder traversal:");
				inOrder(root);//中向遍历
				break;
		case 3: System.out.println("Postorder traversal:");
				postOrder(root);//后向遍历
				break;
		default: System.out.println("Inorder traversal:");
				inOrder(root);
				break;
		}
		System.out.println("");
	}
	
	//前向遍历
	private void preOrder(BNode localRoot) {
		if(localRoot != null) {
			System.out.print(localRoot.data + " ");
			preOrder(localRoot.leftChild);
			preOrder(localRoot.rightChild);
		}
	}
	
	//中向遍历
	private void inOrder(BNode localRoot) {
		if(localRoot != null) {
			inOrder(localRoot.leftChild);
			System.out.print(localRoot.data + " ");
			inOrder(localRoot.rightChild);
		}
	}
	
	//后向遍历
	private void postOrder(BNode localRoot) {
		if(localRoot != null) {
			postOrder(localRoot.leftChild);
			postOrder(localRoot.rightChild);
			System.out.print(localRoot.data + " ");
		}
	}
	
	//查找最小值
	/*根据二叉搜索树的存储规则，最小值应该是左边那个没有子节点的那个节点*/
	public BNode minNumber() {
		BNode current = root;
		BNode parent = root;
		while(current != null) {
			parent = current;
			current = current.leftChild;
		}	
		return parent;
	}
	
	//查找最大值
	/*根据二叉搜索树的存储规则，最大值应该是右边那个没有子节点的那个节点*/
	public BNode maxNumber() {
		BNode current = root;
		BNode parent = root;
		while(current != null) {
			parent = current;
			current = current.rightChild;
		}	
		return parent;
	}
	
	//删除节点
	/*
	 * 删除节点在二叉树中是最复杂的，主要有三种情况：
	 * 1. 该节点没有子节点（简单）
	 * 2. 该节点有一个子节点（还行）
	 * 3. 该节点有两个子节点（复杂）
	 * 删除节点的时间复杂度为O(logN)
	 */
	public boolean delete(int key) {
		BNode current = root;
//		BNode parent = root;
		boolean isLeftChild = true;
		
		if(current == null) {
			return false;
		}
		//寻找要删除的节点
		while(current.data != key) {
//			parent = current;
			if(key < current.key) {
				isLeftChild = true;
				current = current.leftChild;
			}
			else {
				isLeftChild = false;
				current = current.rightChild;
			}
			if(current == null) {
				return false;
			}
		}
		
		//找到了要删除的节点，下面开始删除
		//1. 要删除的节点没有子节点,直接将其父节点的左子节点或者右子节点赋为null即可
		if(current.leftChild == null && current.rightChild == null) {
			return deleteNoChild(current, isLeftChild);
		}
		
		//3. 要删除的节点有两个子节点
		else if(current.leftChild != null && current.rightChild != null) {
			return deleteTwoChild(current, isLeftChild);
		}
		
		//2. 要删除的节点有一个子节点，直接将其砍断，将其子节点与其父节点连起来即可，要考虑特殊情况就是删除根节点，因为根节点没有父节点
		else {
			return deleteOneChild(current, isLeftChild);
		}
		
	}
	
	public boolean deleteNoChild(BNode node, boolean isLeftChild) {
		if(node == root) {
			root = null;
			return true;
		}
		if(isLeftChild) {
			node.parent.leftChild = null;
		}
		else {
			node.parent.rightChild = null;
		}
		return true;
	}
	
	public boolean deleteOneChild(BNode node, boolean isLeftChild) {
		if(node.leftChild == null) {
			if(node == root) {
				root = node.rightChild;
				node.parent = null;
				return true;
			}
			if(isLeftChild) {
				node.parent.leftChild  = node.rightChild;
			}
			else {
				node.parent.rightChild = node.rightChild;
			}
			node.rightChild.parent = node.parent;
		}
		else {
			if(node == root) {
				root = node.leftChild;
				node.parent = null;
				return true;
			}
			if(isLeftChild) {
				node.parent.leftChild  = node.leftChild;
			}
			else {
				node.parent.rightChild = node.leftChild;
			}
			node.leftChild.parent = node.parent;
		}
		return true;
	}
	
	public boolean deleteTwoChild(BNode node, boolean isLeftChild) {
		BNode successor = getSuccessor(node);
		if(node == root) {
			successor.leftChild = root.leftChild;
			successor.rightChild = root.rightChild;
			successor.parent = null;
			root = successor;
		}
		else if(isLeftChild) {
			node.parent.leftChild = successor;
		}
		else {
			node.parent.rightChild = successor;
		}
		successor.leftChild = node.leftChild;//connect successor to node's left child
		return true;
	}
	
	//获得要删除节点的后继节点（中序遍历的下一个节点）
	public BNode getSuccessor(BNode delNode) {
		BNode successor = delNode;
		BNode current = delNode.rightChild;
		while(current != null) {
			successor = current;
			current = current.leftChild;
		}
		if(successor != delNode.rightChild) {
			successor.parent.leftChild = successor.rightChild;
			if(successor.rightChild != null) {		
				successor.rightChild.parent = successor.parent;//删除后续节点在原来的位置
			}
			successor.rightChild = delNode.rightChild;//将后续节点放到正确位置，与右边连上
		}
		return successor;
	}
}

class BNode {
	public int key;
	public double data;
	public BNode parent;
	public BNode leftChild;
	public BNode rightChild;
	
	public void displayNode() {
		System.out.println("{" + key + ":" + data + "}");
	}
}

    二叉树就谈论到这吧，如果有错误之处欢迎留言指正~

_____________________________________________________________________________________________________________________________________________________

-----更多文章请看http://blog.csdn.net/eson_15