CCF 网络延时
| 试题编号： | 201503-4 |
| 试题名称： | 网络延时 |
| 时间限制： | 1.0s |
| 内存限制： | 256.0MB |
| 问题描述： |
问题描述
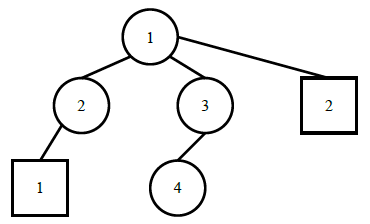
给定一个公司的网络，由n台交换机和m台终端电脑组成，交换机与交换机、交换机与电脑之间使用网络连接。交换机按层级设置，编号为1的交换机为根交换机，层级为1。其他的交换机都连接到一台比自己上一层的交换机上，其层级为对应交换机的层级加1。所有的终端电脑都直接连接到交换机上。
当信息在电脑、交换机之间传递时，每一步只能通过自己传递到自己所连接的另一台电脑或交换机。请问，电脑与电脑之间传递消息、或者电脑与交换机之间传递消息、或者交换机与交换机之间传递消息最多需要多少步。
输入格式
输入的第一行包含两个整数n, m，分别表示交换机的台数和终端电脑的台数。
第二行包含n - 1个整数，分别表示第2、3、……、n台交换机所连接的比自己上一层的交换机的编号。第i台交换机所连接的上一层的交换机编号一定比自己的编号小。 第三行包含m个整数，分别表示第1、2、……、m台终端电脑所连接的交换机的编号。
输出格式
输出一个整数，表示消息传递最多需要的步数。
样例输入
4 2
1 1 3 2 1
样例输出
4
样例说明
样例的网络连接模式如下，其中圆圈表示交换机，方框表示电脑：
 其中电脑1与交换机4之间的消息传递花费的时间最长，为4个单位时间。
样例输入
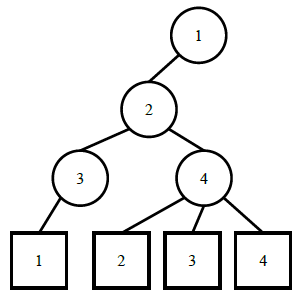
4 4
1 2 2 3 4 4 4
样例输出
4
样例说明
样例的网络连接模式如下：
 其中电脑1与电脑4之间的消息传递花费的时间最长，为4个单位时间。
评测用例规模与约定
前30%的评测用例满足：n ≤ 5, m ≤ 5。
前50%的评测用例满足：n ≤ 20, m ≤ 20。 前70%的评测用例满足：n ≤ 100, m ≤ 100。 所有评测用例都满足：1 ≤ n ≤ 10000，1 ≤ m ≤ 10000。 |
开始确实没什么思路，直接DFS暴搜了一下....
果然可以对70%的数据
于是参考了一下其他资料，这道题是求树的直径
现有如下结论
主要是利用了反证法：
假设 s-t这条路径为树的直径，或者称为树上的最长路
现有结论，从任意一点u出发搜到的最远的点一定是s、t中的一点，然后在从这个最远点开始搜，就可以搜到另一个最长路的端点，即用两遍广搜就可以找出树的最长路
证明：
1 设u为s-t路径上的一点，结论显然成立，否则设搜到的最远点为T则
dis(u,T) >dis(u,s) 且 dis(u,T)>dis(u,t) 则最长路不是s-t了，与假设矛盾
2 设u不为s-t路径上的点
首先明确，假如u走到了s-t路径上的一点，那么接下来的路径肯定都在s-t上了，而且终点为s或t，在1中已经证明过了
所以现在又有两种情况了：
1：u走到了s-t路径上的某点，假设为X，最后肯定走到某个端点，假设是t ，则路径总长度为dis(u,X)+dis(X,t)
2：u走到最远点的路径u-T与s-t无交点，则dis(u-T) >dis(u,X)+dis(X,t);显然，如果这个式子成立，
则dis(u,T)+dis(s,X)+dis(u,X)>dis(s,X)+dis(X,t)=dis(s,t)最长路不是s-t矛盾
再用一遍BFS即可以求出最长路径
AC代码如下：
#include <iostream>
#include <vector>
#include <string.h>
#include <queue>
#define N 20005
using namespace std;
int v[N];
int d[N];
vector<int> G[N];
queue<int> q;
int n,m,answer=0,p;
void BFS(int st)
{
int vis;
memset(v,0,sizeof(v));
memset(d,0,sizeof(d));
q.push(st);
v[st]=1;
while(!q.empty())
{
st=q.front();
q.pop();
for(int j=0;j<G[st].size();j++)
{
vis=G[st][j];
if(v[vis]==0)
{
v[vis]=1;
d[vis]=d[st]+1;
q.push(vis);
if(answer<d[vis])
{
answer=d[vis];
p=vis;
}
}
}
}
}
int main()
{
int x,sign=1;
cin>>n>>m;
for(int i=0;i<n-1;i++)
{
cin>>x;
G[x].push_back(++sign);
G[sign].push_back(x);
}
for(int i=0;i<m;i++)
{
cin>>x;
G[x].push_back(++sign);
G[sign].push_back(x);
}
BFS(1);
BFS(p);
cout<<answer<<endl;
return 0;
}