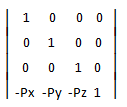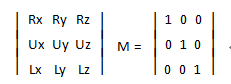【D3D11游戏编程】学习笔记二十:第一人称摄像机的实现
(注:【D3D11游戏编程】学习笔记系列由CSDN作者BonChoix所写,转载请注明出处:http://blog.csdn.net/BonChoix,谢谢~)
在这篇文章中,我们来实现一个简单的第一个称摄像机。在之前所有的程序中,为了方便从各个角度观察场景,我们可以通过鼠标来旋转视角和镜头远近。尽管相对单一地从固定的角度观察方便多了,但观察点依然仅仅限制在一个球面上,观察目标点始终为场景原点。有了今天这个摄像机,我们将可以在场景中随意走动、从任一角度进行观察,正如在第一人称射击游戏中一样。
1. 坐标变换的一点回顾
要实现一个FPS摄像机,首先必须要对3D中的坐标变换有着非常清晰的认识。在该系列文章一开始介绍3D渲染管线时,我们提到过,在3D世界中,有几种不同的坐标系。首先是模型坐标系(Model Space),该坐标系以模型中心为原点,这样最大的好处在于大大方便了模型的制作,而不需要考虑该模型在场景中可能出现的不同位置。模型中的各个坐标以该坐标系为基准,一旦模型制作完成,其顶点即固定了; 当然,在3D场景中,各个物体有着各自不同的位置,且同一个模型也可能出现在场景中不同的位置,从场景的角度出发,为了表示各个物体的不同位置,则需要用到世界坐标系(World Space),把模型从模型坐标系转换到世界坐标系中用到的变换即“世界变换”;在任一时刻,呈现在屏幕上的场景部分,是通过场景中的一个虚拟摄像机拍照后得到的。摄像机在场景中不同的位置、不同的摆放角度,都会导致拍摄到的场景不一样。这一点很好理解,可以想象自己用照相机拍照的情景。换句话说,这时候,我们需要以摄像机为参考点来观察场景,这种情况下使用的坐标系即视角坐标系(View Space)。把模型从世界坐标系转换到视角坐标系用到的变换即“视角变换”。一个摄像机在任一时候能够观察到的场景范围取决于它本身的几项参数:观察角(一般指定为Y轴方向),投影长、宽比,最近、最远距离。通过这几项参数,摄像机所能观察到的场景即被限制在一个被切掉顶部的金字塔形状的几何体内,我们称之为“平截头体”(Frustum)。位于之内的物品将被观察到,之外的物品会被剔除,而部分位于之内的物品将会被进行裁剪(Clipping)。当然,如果直接利用平截头体进行裁剪操作,计算会十分麻烦,这时就要用到”投影变换“了,通过投影变换,该平截头体变为一个标准的立方体,长、宽位于[-1, 1]之间,z坐标位于[0, 1]之间,这时所在的坐标系空间,我们称之为”投影空间“(Projection Space)。投影空间有两大关键作用:一是方便了接下来的裁剪操作,因为这时的视景体位于一个标准立方体内,因此计算大大被简化了;二是通过3D场景中的3维坐标得到了投影后的二维坐标,以用于之后的光栅化阶段。
注意:很多人对于投影变换存在着误解,认为经过投影变换后3D坐标即变为了2维变换,z分量就丢弃了。其实这是不对的,经过投影变换后z坐标依然在在(位于[0, 1]之间),而且还将发挥相当重要的作用,即利用z坐标作为深度判断的依据。
2. 摄像机视角矩阵的生成
在进行完简要的回顾后,我们把注意力集中在视角空间及视角变换上来。刚才提到,摄像机在空间有着特定的位置及朝向,它所观察到的物体取决于物体与摄像机的相对位置。为了表示摄像机位置,我们可以使用一个3维向量;对于摄像机的的朝向,可以使用三个相互垂直的坐标轴的惟一地确定,即右、上、前三个方向。以摄像机为参考点,即以之为原点来观察物体。因此,视角变换,本质上即把场景中所有的物体、连同摄像机,使用相同的变换,使得变换后摄像机位于场景的原点,且其三个坐标轴(右、上、前)与世界坐标系的X、Y、Z坐标轴重合。这时,变换后的所有物体的坐标值,即变为与摄像机的相对位置了。
我们把摄像机位置用[ px, py, pz ]来表示,其三个表示朝向的坐标轴分别表示为[ Rx, Ry, Rz ]、[ Ux, Uy, Uz ]、[ Lx, Ly, Lz ]。而视角变换的目的即把它的这些参数转换为:位置[ 0, 0, 0 ],以及三个坐标轴:[ 1, 0,0 ]、[ 0, 1, 0 ]、 [ 0, 0, 1 ]。由于有平移和旋转同时存在,因此该变换可以分为两步进行:1. 平移到原点;2. 旋转。
平移操作很简单,即把[Px,Py, Pz,1]移回到原点,矩阵为:
旋转操作需要点小技巧。我们的目的是把三个轴分别转换成[1,0,0]、[0,1,0]、[0,0,1],令旋转矩阵为M,可以表示为如下所示:
由上面式子可以看出,左边的矩阵与M相乘后变为右边的单位矩阵。这正是关键所在!我们知道,一个矩阵与它的逆矩阵相乘结果为单位矩阵,因此,要求矩阵M,我们可以求它的逆矩阵。求逆矩阵需要大量的计算,有没有更好的方法?
答案是有的!有一点需要知道,正交矩阵的逆矩阵等于它的转置矩阵。而正交矩阵的一个特点:正交矩阵的每行(每列)相互垂直。回来看下我们左边的矩阵,每行分别对应了摄像机的三个相互垂直的轴,显然它正是正交矩阵!好了,这下M的计算,就变成求它的转置矩阵了。而转置的计算再简单不过了,直接给出:
现在,两步需要的矩阵都有了,那最终的视角矩阵即两次转换的乘积,当然,由于平移变换的存在,现在要在4x4矩阵了,如下所示:
结果中P*R、P*U、P*L分别是位置向量与R、U、L三个向量的点积,通过查看左边的矩阵相乘很容易看出来。
OK, 视角矩阵的推导完毕,现在我们知道:
任一时刻,通过摄像机位置P(Px,Py,Pz),以及三个坐标轴(R,U,L),可以得到当前的视角变换矩阵:
3. 摄像机类:Camera
有了以上的基础,现在可以来设计我们的FPS摄像机类了。这个摄像机功能比较简单,可以进行的操作有:
移动操作:前进、后退;左、右平移;
视角旋转操作:左、右扭头;上、下点头;
该摄像机有如下参数:
1. 首先,核心的参数当然是用来生成视角矩阵的:摄像机位置以及三个坐标轴;
2. 此外,用来控制摄像机可视范围(即生成投影矩阵)的参数有:视角大小、投影面宽高比、远平面和近平面。
根据以上描述,我们的摄像机类定义如下:
class Camera
{
public:
Camera();
//设置摄像机位置
void SetPosition(float x, float y, float z) { m_position = XMFLOAT3(x,y,z); }
void SetPositionXM(FXMVECTOR pos) { XMStoreFloat3(&m_position,pos); }
//获得摄像位置及朝向相关参数
XMFLOAT3 GetPosition() const { return m_position; }
XMFLOAT3 GetRight() const { return m_right; }
XMFLOAT3 GetUp() const { return m_up; }
XMFLOAT3 GetLook() const { return m_look; }
XMVECTOR GetPositionXM() const { return XMLoadFloat3(&m_position); }
XMVECTOR GetRightXM() const { return XMLoadFloat3(&m_right); }
XMVECTOR GetUpXM() const { return XMLoadFloat3(&m_up); }
XMVECTOR GetLookXM() const { return XMLoadFloat3(&m_look); }
//获得投影相关参数
float GetNearZ() const { return m_nearZ; }
float GetFarZ() const { return m_farZ; }
float GetFovY() const { return m_fovY; }
float GetFovX() const { return atan(m_aspect * tan(m_fovY * 0.5f)) * 2.f; }
float GetAspect() const { return m_aspect; }
//获得相关矩阵
XMMATRIX View() const { return XMLoadFloat4x4(&m_view); }
XMMATRIX Projection() const { return XMLoadFloat4x4(&m_proj); }
XMMATRIX ViewProjection() const { return XMLoadFloat4x4(&m_view) * XMLoadFloat4x4(&m_proj); }
//设置投影相关参数
void SetLens(float fovY, float ratioAspect, float nearZ, float farZ)
{
m_fovY = fovY;
m_aspect = ratioAspect;
m_nearZ = nearZ;
m_farZ = farZ;
}
//通过位置+观察点来设置视角矩阵
void LookAtXM(FXMVECTOR pos, FXMVECTOR lookAt, FXMVECTOR worldUp);
void LookAt(XMFLOAT3 &pos, XMFLOAT3 &lookAt, XMFLOAT3 &worldUp);
//基本操作
void Walk(float dist); //前后行走
void Strafe(float dist); //左右平移
void Pitch(float angle); //上下点头
void RotateY(float angle); //左右插头
//更新相关矩阵
void UpdateView();
private:
XMFLOAT3 m_right; //位置及三个坐标轴参数
XMFLOAT3 m_up;
XMFLOAT3 m_look;
XMFLOAT3 m_position;
float m_aspect; //投影相关参数
float m_fovY;
float m_nearZ;
float m_farZ;
XMFLOAT4X4 m_view; //视角矩阵
XMFLOAT4X4 m_proj; //投影矩阵
};
类中针对Set和Get相关函数分别提供了针对XMVECTOR/XMMATRIX型的参数以及针对XMFLOAT3/XMFLOAT4X4型参数的版本,可以根据情况先把更方便的选择使用。这里面大部分函数功能十分明显易懂,这里只针对基本操作函数进行下解释:
Walk函数:
该函数功能在于沿观察方向前进或后退。因此本质m_pos沿m_look方向进行dist的平移。操作如下:
void Camera::Walk(float dist)
{
XMVECTOR pos = XMLoadFloat3(&m_position);
XMVECTOR look = XMLoadFloat3(&m_look);
pos += look * XMVectorReplicate(dist);
XMStoreFloat3(&m_position,pos);
}
Strafe函数同理,用于左右平移,即m_pos沿m_right方向进行dist的平移:
void Camera::Strafe(float dist)
{
XMVECTOR pos = XMLoadFloat3(&m_position);
XMVECTOR right = XMLoadFloat3(&m_right);
pos += right * XMVectorReplicate(dist);
XMStoreFloat3(&m_position,pos);
}
Pitch(float angle)函数,用于上下点头来调整视角,本质上即把m_up向量沿m_right向量进行angle的旋转:
void Camera::Pitch(float angle)
{
XMMATRIX rotation = XMMatrixRotationAxis(XMLoadFloat3(&m_right),angle);
XMStoreFloat3(&m_up,XMVector3TransformNormal(XMLoadFloat3(&m_up),rotation));
XMStoreFloat3(&m_look,XMVector3TransformNormal(XMLoadFloat3(&m_look),rotation));
}
RotateY(float angle)函数,用于摇头以旋转视角,本质上即所有三个坐标轴(m_right, m_up, m_look)沿Y轴方向进行angle的旋转:
void Camera::RotateY(float angle)
{
XMMATRIX rotation = XMMatrixRotationY(angle);
XMStoreFloat3(&m_right,XMVector3TransformNormal(XMLoadFloat3(&m_right),rotation));
XMStoreFloat3(&m_up,XMVector3TransformNormal(XMLoadFloat3(&m_up),rotation));
XMStoreFloat3(&m_look,XMVector3TransformNormal(XMLoadFloat3(&m_look),rotation));
}
UpdateView()函数,用于在上述等操作结束后,根据新的参数来更新视角矩阵,生成方法即与我们刚刚推导的一样,相关函数如下:
void Camera::UpdateView()
{
XMVECTOR r = XMLoadFloat3(&m_right);
XMVECTOR u = XMLoadFloat3(&m_up);
XMVECTOR l = XMLoadFloat3(&m_look);
XMVECTOR p = XMLoadFloat3(&m_position);
r = XMVector3Normalize(XMVector3Cross(u,l));
u = XMVector3Normalize(XMVector3Cross(l,r));
l = XMVector3Normalize(l);
float x = -XMVectorGetX(XMVector3Dot(p,r));
float y = -XMVectorGetX(XMVector3Dot(p,u));
float z = -XMVectorGetX(XMVector3Dot(p,l));
XMStoreFloat3(&m_right,r);
XMStoreFloat3(&m_up,u);
XMStoreFloat3(&m_look,l);
XMStoreFloat3(&m_position,p);
m_view(0,0) = m_right.x; m_view(0,1) = m_up.x; m_view(0,2) = m_look.x; m_view(0,3) = 0;
m_view(1,0) = m_right.y; m_view(1,1) = m_up.y; m_view(1,2) = m_look.y; m_view(1,3) = 0;
m_view(2,0) = m_right.z; m_view(2,1) = m_up.z; m_view(2,2) = m_look.z; m_view(2,3) = 0;
m_view(3,0) = x; m_view(3,1) = y; m_view(3,2) =z; m_view(3,3) = 1;
}
这里要注意的是,在生成矩阵之前,要先对三个向量进行正交化以及归一化。
为什么有这个必要呢?主要原因在于经过大量的旋转等操作后,由于浮点数精度的问题,可能导致三个向量的长度不再为1,而且不再相互垂直。如果一直这样下去,后面的误差将会越来越大。因此,在每次更新矩阵时,我们就将其修正一次。修正方法很简单,如代码所示:通过两次叉乘保证正交化,通过Normalize来归一化。
4. 摄像机类的使用
摄像机类的设计就是这样。函数的定义基本是自解释的,因此使用起来应该是非常简单。
初始化阶段首先要做的应该是设置好投影相关参数,即SetLens函数。在前面大量使用XMMatrixPerspectiveFovLH函数后,应该非常清楚这里的参数了吧。
如果依然想使用类似XMMatrixLookAtLH函数来设置视角矩阵,可以使用LookAt或LookAtXM函数,参数完全一样;
此外,该类还提供了直接任意来摆放摄像机的函数,即通过SetPosition来指定其位置,在场景中通过基本操作函数随意地走动、旋转视角。
在每一帧更新阶段,记得调用UpdateView函数来更新当前的视角矩阵。
如果想获得当前的相关矩阵,可以直接调用相关函数(View、ViewProjection、Projection)来获取。
最后注意的是,由于我们的程序框架可以在随时改变窗口大小,每次改变后程序都会调用OnResize()函数来更新后缓冲区及深度/模板缓冲区。因此也应该调用摄像机中的SetLens函数来相应地更新投影相关参数,以适应当前窗口的尺寸。
好啦,使用就是这么简单,在后面的程序中,就可以使用这个类在场景中随意走动啦~
5. 示例程序
本节的示例程序很简单,没有什么新的渲染技术,仅仅用来测试一下我们崭新的摄像机。
使用鼠标左键来任意旋转镜头, 键盘通过'W','A','S',D'键来前、后、左、右移动。
除了换成Camera类来控制视角、投影矩阵外,其他部分代码思路跟前面的程序完全一样。为了突出Camera类的使用地方,仅仅针对Camera使用部分添加了注释。
示例程序代码
本文完