计算机视觉与模式识别（3）—— FaceMorphing

        这是一个非常有意思的应用，可以将一个人的脸逐渐过渡为另一个人的脸。花了大概1天完成了最基本的功能，大概3天去完善它，可能还有不少bug等着我去修改，不过先把目前的进展记录下来吧。

        图形库：CImg

        环境：Win10、C++11、VS2013

        效果图一：

        效果图二：

思路：

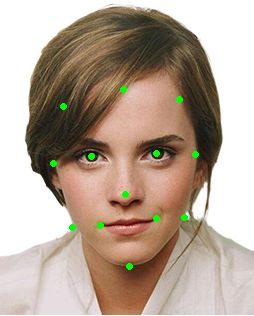
1)      分别对图像A和图像B采集控制点（坐标）

2)      利用Delaunay算法划分三角形，保证图像A和图像B的三角形一一对应且不重合。

3)      计算每对三角形的过渡三角形，过渡量为0~1。

4)      计算三角形到三角形的仿射变换矩阵。

5)      利用变换矩阵分别将图像A和图像B变换到过渡三角形网格。

6)      利用过渡量计算合成图的像素色彩。

        我觉得难点主要在于 Delaunay算法 和 Affine Transformation矩阵计算，其次是应用的鲁棒性增强。由于目前还没有学习人脸识别的相关技术，所以还需要人为标定控制点，做一些“Dirty Work”。因此我也把工程分为了两个：一是主工程，专门负责已经三角分割后的图像处理。二是辅助工程，专门负责控制点的采集以及三角分割。可以这么说，主工程的核心是Morphing，辅助工程的核心是Delaunay。

        先看看辅助工程吧，事先定义好了常用的结构体后，就可以写Delaunay算法了。Delaunay分割的准则是：任何三角形ABC，不存在一点D，在其外接圆内。考虑到人脸的控制点数量一般在低两位数，计算机平均每秒可计算百万级别的数据，也就是支持每秒O(n^4)的计算量，那么可以采用暴力算法：

void Delaunay::buildDelaunayEx(const std::vector<Dot*>& vecDot, std::vector<Triangle*>& vecTriangle)
{
	int size = vecDot.size();
	if (size < 3)return;
	
	for (int i = 0; i < size - 2; ++i)
	{
		for (int j = i + 1; j < size - 1; ++j)
		{
			for (int k = j + 1; k < size; ++k)
			{
				Dot* A = vecDot[i];
				Dot* B = vecDot[j];
				Dot* C = vecDot[k];
				Triangle* tri = new Triangle(*A, *B, *C);
				getTriangleCircle(*tri);

				bool find = true;
				for (int m = 0; m < size; ++m)
				{
					Dot* P = vecDot[m];
					if (*P == *A || *P == *B || *P == *C) continue;	
					if (pointInCircle(*P))
					{
						find = false;
						break;
					}
				}
				if (find)
				{
					vecTriangle.push_back(tri);
				}
			}
		}
	}
}

        我试了一下在控制点不超过40个时，是可以1秒跑完的。当然啦，这是一种最笨最简单的方法。
        为了让图像A和图像B的三角分割是一一对应的，我只对图像A进行了Delaunay分割，而图像B则根据图像A的三角构成来分割。因此，我会记录图像A的每个点的序号，以及每个三角形三个点的序号组成。最终将这些序号以文本的方式输出。

#include "CImg.h"
#include "Delaunay.h"
using namespace cimg_library;

#include <iostream>
#include <fstream>
#include <string>
using namespace std;

int main()
{
	// 输入图像路径
	string pathA, pathB;
	cout << "Image A path: "; cin >> pathA;
	cout << "Image B path: "; cin >> pathB;

	CImg<double> sourceA(pathA.c_str()), sourceB(pathB.c_str());
	CImgDisplay Adisp(sourceA, "Image A"), Bdisp(sourceB, "Image B");

	// 控制点数组
	vector<Dot*> vecDotA, vecDotB;

	// 图像角点预先置入数组
	vecDotA.push_back(new Dot(0, 0, 0));
	vecDotA.push_back(new Dot(0, sourceA.height() - 1, 1));
	vecDotA.push_back(new Dot(sourceA.width() - 1, sourceA.height() - 1, 2));
	vecDotA.push_back(new Dot(sourceA.width() - 1, 0, 3));

	vecDotB.push_back(new Dot(0, 0, 0));
	vecDotB.push_back(new Dot(0, sourceB.height() - 1, 1));
	vecDotB.push_back(new Dot(sourceB.width() - 1, sourceB.height() - 1, 2));
	vecDotB.push_back(new Dot(sourceB.width() - 1, 0, 3));

	// 点线颜色
	int color[3] = { 0, 255, 0 };

	// 点击鼠标获取坐标
	while (!Adisp.is_closed())
	{
		Adisp.wait();
		if (Adisp.button() & 1 && Adisp.mouse_y() >= 0)
		{
			Dot* click = new Dot(Adisp.mouse_x(), Adisp.mouse_y(), vecDotA.size());
			sourceA.draw_circle(click->x, click->y, sourceA.width() / 40, color);
			sourceA.display(Adisp);
			vecDotA.push_back(click);
		}
	}

	while (!Bdisp.is_closed())
	{
		Bdisp.wait();
		if (Bdisp.button() & 1 && Bdisp.mouse_y() >= 0)
		{
			Dot* click = new Dot(Bdisp.mouse_x(), Bdisp.mouse_y(), vecDotB.size());
			sourceB.draw_circle(click->x, click->y, sourceB.width() / 40, color);
			sourceB.display(Bdisp);
			vecDotB.push_back(click);
		}
	}

	// 三角形数组
	vector<Triangle*> vecTriA, vecTriB;

	// 对图像A进行Delaunay三角形分割
	 Delaunay().buildDelaunayEx(vecDotA, vecTriA);

	// 同步图像B的三角形分割
	 for (int i = 0; i < vecTriA.size(); ++i)
	 {
		 Dot* A = vecDotB[vecTriA[i]->a.value];
		 Dot* B = vecDotB[vecTriA[i]->b.value];
		 Dot* C = vecDotB[vecTriA[i]->c.value];
		 vecTriB.push_back(new Triangle(*A, *B, *C));
	 }

	 CImg<double> targetA(pathA.c_str()), targetB(pathB.c_str());
	 CImgDisplay TAdisp(targetA), TBdisp(targetB);

	// 点击鼠标逐步显示三角形
	int i = 0;
	while (!TAdisp.is_closed())
	{
		TAdisp.wait();
		if (TAdisp.button() && i < vecTriA.size())
		{
			targetA.draw_line(vecTriA[i]->a.x, vecTriA[i]->a.y, vecTriA[i]->b.x, vecTriA[i]->b.y, color);
			targetA.draw_line(vecTriA[i]->a.x, vecTriA[i]->a.y, vecTriA[i]->c.x, vecTriA[i]->c.y, color);
			targetA.draw_line(vecTriA[i]->b.x, vecTriA[i]->b.y, vecTriA[i]->c.x, vecTriA[i]->c.y, color);
			targetA.display(TAdisp);
			targetB.draw_line(vecTriB[i]->a.x, vecTriB[i]->a.y, vecTriB[i]->b.x, vecTriB[i]->b.y, color);
			targetB.draw_line(vecTriB[i]->a.x, vecTriB[i]->a.y, vecTriB[i]->c.x, vecTriB[i]->c.y, color);
			targetB.draw_line(vecTriB[i]->b.x, vecTriB[i]->b.y, vecTriB[i]->c.x, vecTriB[i]->c.y, color);
			targetB.display(TBdisp);
			++i;
		}
	}

	// 获取图像命名, 改变命名为txt格式
	string filenameA = pathA.substr(0, pathA.find_last_of(".")) + ".txt";
	string filenameB = pathB.substr(0, pathB.find_last_of(".")) + ".txt";

	// 控制点和三角形写入文本
	ofstream outputA(filenameA, ios::out), outputB(filenameB, ios::out);
	outputA << "[Points]" << endl;
	outputB << "[Points]" << endl;
	for (int i = 0; i < vecDotA.size(); ++i)
	{
		outputA << vecDotA[i]->x << "," << vecDotA[i]->y << endl;
		outputB << vecDotB[i]->x << "," << vecDotB[i]->y << endl;
	}
	outputA << "[Triangles]" << endl;
	outputB << "[Triangles]" << endl;
	for (int i = 0; i < vecTriA.size(); ++i)
	{	
		outputA << vecTriA[i]->a.value << "," << vecTriA[i]->b.value << "," << vecTriA[i]->c.value << endl;	
		outputB << vecTriB[i]->a.value << "," << vecTriB[i]->b.value << "," << vecTriB[i]->c.value << endl;
	}
}

        接下来是主工程，有了辅助工程提供的文本数据以后，主工程需要计算每对三角的过渡三角形：

// 计算过渡三角形
Triangle* middleTriangle(Triangle* A, Triangle* B, float rate)
{
	float ax = rate*(A->a.x) + (1 - rate)*(B->a.x);
	float ay = rate*(A->a.y) + (1 - rate)*(B->a.y);
	float bx = rate*(A->b.x) + (1 - rate)*(B->b.x);
	float by = rate*(A->b.y) + (1 - rate)*(B->b.y);
	float cx = rate*(A->c.x) + (1 - rate)*(B->c.x);
	float cy = rate*(A->c.y) + (1 - rate)*(B->c.y);
	return new Triangle(Dot(ax, ay), Dot(bx, by), Dot(cx, cy));
}

        然后计算变换矩阵系数：

Matrix3x3 Warp::TriangleToTriangle(float u0, float v0, float u1, float v1, float u2, float v2,
	float x0, float y0, float x1, float y1, float x2, float y2)
{
	// |A|
	int detA;
	detA = u0*v1 + u1*v2 + u2*v0 - u2*v1 - u0*v2 - u1*v0;
	// A*
	int A11, A12, A13, A21, A22, A23, A31, A32, A33;
	A11 = v1 - v2;
	A21 = -(v0 - v2);
	A31 = v0 - v1;
	A12 = -(u1 - u2);
	A22 = u0 - u2;
	A32 = -(u0 - u1);
	A13 = u1*v2 - u2*v1;
	A23 = -(u0*v2 - u2*v0);
	A33 = u0*v1 - u1*v0;

	Matrix3x3 result;
	result.a11 = (float)(x0*A11 + x1*A21 + x2*A31) / detA;
	result.a21 = (float)(y0*A11 + y1*A21 + y2*A31) / detA;
	result.a31 = (float)(A11 + A21 + A31) / detA;
	result.a12 = (float)(x0*A12 + x1*A22 + x2*A32) / detA;
	result.a22 = (float)(y0*A12 + y1*A22 + y2*A32) / detA;
	result.a32 = (float)(A12 + A22 + A32) / detA;
	result.a13 = (float)(x0*A13 + x1*A23 + x2*A33) / detA;
	result.a23 = (float)(y0*A13 + y1*A23 + y2*A33) / detA;
	result.a33 = (float)(A13 + A23 + A33) / detA;
	return result;
}

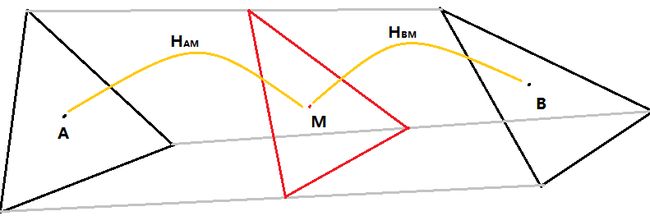
        计算过渡三角形变换矩阵的目的是，把原图像转换为过渡图像，使得两幅原图像在一致的三角网格下进行色彩叠加(Morph)。为了达到这个目的，需要把原图像的三角网格利用变换矩阵映射到过渡三角形网格上。每一对三角形有一个变换矩阵，存入动态数组中。

// 计算三角变换矩阵
vector<Matrix3x3*> vecAB, vecBA;
for (int i = 0; i < vecTriA.size(); ++i)
{
	Matrix3x3 HAM = Warp::TriangleToTriangle(*vecTriA[i], *vecTriM[i]);
	vecAB.push_back(new Matrix3x3(HAM));
	Matrix3x3 HBM = Warp::TriangleToTriangle(*vecTriB[i], *vecTriM[i]);
	vecBA.push_back(new Matrix3x3(HBM));
}

         三角映射比较简单了，判断每个像素点是否在原三角形内，然后计算映射三角形内的坐标，最后把该坐标的像素在原图上做一个双线性插值计算，就可以作为该目标像素点的色彩值了。以图像A为例：

// 对原图A进行三角变换
cimg_forXY(targetA, x, y)
{
	bool isFind = false;
	for (int i = 0; i < vecTriB.size(); ++i)
	{
		if (vecTriB[i]->pointInTriangle(Dot(x, y)))
		{
			float tx = x*vecBA[i]->a11 + y*vecBA[i]->a12 + vecBA[i]->a13;
			float ty = x*vecBA[i]->a21 + y*vecBA[i]->a22 + vecBA[i]->a23;
			if (tx >= 0 && tx < width && ty >= 0 && ty < height)
			{
				cimg_forC(sourceA, c)
					targetA(x, y, 0, c) = sourceA.linear_atXY(tx, ty, 0, c);
			}
			isFind = true;
			break;
		}
	}
	if (!isFind)
	{
		cimg_forC(sourceA, c)
			targetA(x, y, 0, c) = sourceA.linear_atXY(x, y, 0, c);
	}
}

        最后合成目标图的像素色彩：

// 计算色彩插值
cimg_forXYZC(target, x, y, z, c)
	target(x, y, z, c) = rate*targetB(x, y, z, c) + (1 - rate)*targetA(x, y, z, c);

       

         到此，应用已经基本成型。更多的测试还在进行中，我希望最终能通过Canvas制作成网页版的变脸应用。