（1.2.2.1）栈和队列的应用：数制转换、括号匹配、后缀表达式求解，中缀表达式求解、双栈实现队列，min函数栈

（1）数制转换

void conversion(int a,int b)                     // 实现进制转换
{
    int stack[maxsize];

    int top=-1;
    while(a)
    {
        stack[++top]=a%b;
        a=a/b;
    }
    while(top!=-1)
    {
        i=stack[top--];
        printf("%d",i);
    }
}

（2）括号匹配

int match(char exp[], int n){

char st[max];int top=-1;// 初始化栈

for（int i=1;i<=n;++i）{

if(exp[i]=='(')  st[++top]="(";

if(exp[i]==')') {

if(top==-1) return 0;

else --top;

}

if(top==-1)return 1;

else return 0;

}

}

（3）后缀表达式求解

     1）中缀表达式  （a+b+c*d）/e

           前缀表达式  /++ab*cde   根左右

          后缀表达式  abcd*++e/   左右跟

     2）多个后缀表达式可能对应一个中缀表达式

     3）后缀表达式在计算过程中，不需要计算运算符的优先级

     4）后缀表达式计算方法：1、取了数字则压栈  2、取了运算符则立即计算

for（i=0;exp[i]!='\0';++i）{

if（exp[i]>'0'&&exp[i]<='9'）//取了数字则压栈

stack[++top]=exp[i];

else{                                       //取了运算符则立即计算

op=exp[i];

b=stack[top--];c=stack[top--];

c=b op a;

st[++top]=c;

}

retrun st[top];

}      

（4）中缀表达式求解

    1.取得操作数则入操作数栈    2.取得运算符  （判断优先是否大于运算符栈的顶部元素）？入操作符栈下一步：取值计算  相等的话，操作符出栈

 void evaluateExpression()   //计算
 {
     stack<char> opan,opat;    //构建两个栈 operand:操作数，operator:操作符
     opat.push('#');    // # 压入符号栈，作为界限符
     cout << "输入算术表达式" << endl;
     char op,a,b,c;
     c=getchar();
     while (c != '#' || opat.top() != '#')  //没有读到 '#'，或者符号栈也没空，则继续读取字符
     {
         //对读入的字符进行判断：是操作数还是操作符？
         if (!isOpat(c))  //是操作数则压入操作数栈
         {
             opan.push(c);
             c = getchar();
         }
         else   //若是操作符，则需把符号栈顶的操作符与当前读入的操作符，进行优先级比较
         {
             switch(getPriority(opat.top(), c))
             {
             case 1:
                 op = opat.top(); opat.pop();
                 b = opan.top(); opan.pop();
                 a = opan.top(); opan.pop();
                 opan.push(char(compute(a,op,b)+'0'));
                 break;
             case 2:
                 opat.push(c);
                 c = getchar();
                 break;
             case 3:
                 opat.pop();
                 c = getchar();
                 break;
             case 0:
                 cout << "错误！" << endl;
                 exit(0);
             }
         }
     }
     cout << "= " << opan.top()-'0' << endl;
 }

（5）双栈队列

已知下面Stack类及其3个方法Push、Pop和 Count，请用2个Stack实现Queue类的入队(Enqueue)出队(Dequeue)方法。

class Stack

{

…

public:

         void Push(int x); // Push an element in stack;

         int Pop();  // Pop an element out of stack;

         int Count() const;     // Return the number of the elements in stack;

…

};

class Queue

{

…

public:

         void Enqueue(int x);

         int Dequeue();

 

private:

         Stack s1;

         Stack s2;

…

};

大多数人的思路是：

（1）始终维护s1作为存储空间，以s2作为临时缓冲区。

（2）入队时，将元素压入s1。

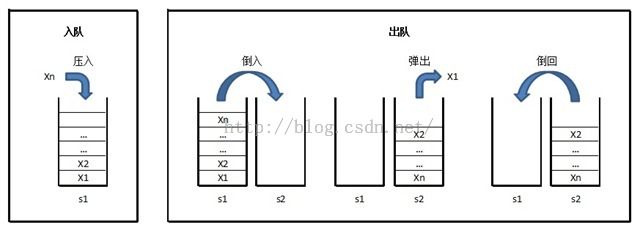
（3）出队时，将s1的元素逐个“倒入”（弹出并压入）s2，将s2的顶元素弹出作为出队元素

（4）之后再将s2剩下的元素逐个“倒回”s1。

有一个细节是可以优化一下的：（3）将s1的元素逐个“倒入”s2时，原在s1栈底的元素，不用“倒入”s2（即只“倒”s1.Count()-1个），可直接弹出作为出队元素返回。这样可以减少一次压栈的操作

上述思路，有些变种，如：

【懒人操作-单栈法】 适合连续出，或者连续入栈的操作。如果赶上下次还是出队操作，效率会高一些，但下次如果是入队操作，效率不如第一种方法。

入队时，先判断s1是否为空，如不为空，说明所有元素都在s1，此时将入队元素直接压入s1；如为空，要将s2的元素逐个“倒回”s1，再压入入队元素。

出队时，先判断s2是否为空，如不为空，直接弹出s2的顶元素并出队；如为空，将s1的元素逐个“倒入”s2，把最后一个元素弹出并出队。

真正性能较高的，其实是另一个变种。即：

【双栈共存法】

入队时，将元素压入s1。

出队时，判断s2是否为空，如不为空，则直接弹出顶元素；如为空，则将s1的元素逐个“倒入”s2，把最后一个元素弹出并出队。

这个思路，避免了反复“倒”栈，仅在需要时才“倒”一次。但在实际面试中很少有人说出，可能是时间较少的缘故吧。

（6）min函数栈

 定义栈的数据结构，要求添加一个min函数，能够得到栈的最小元素。 要求函数min、push以及pop的时间复杂度都是O(1)。

思路1：使用一个辅助栈来保存最小元素，这个解法简单不失优雅。设该辅助栈名字为minimum stack，其栈顶元素为当前栈中的最小元素。

            要获取当前栈中最小元素，只需要返回minimum stack的栈顶元素即可。

            每次执行push操作，检查push的元素是否小于或等于minimum stack栈顶元素。如果是，则也push该元素到minimum stack中。【也可以是位置】；如果不是，再push一次栈顶元素；

            当执行pop操作的时候，每次pop一个元素出栈的时候，同时pop辅助栈。

思路2：同样需要记录每插入一个值后最小值的位置（n个值就要记录n个最小位置），但是这些最小位置不再放在一个辅助栈中，而是在原来的栈节点的数据结构中加入一个指针变量（指向栈节点），用来指示“此时”的最小值节点。