德卡斯特里奥算法(De Casteljau’s Algorithm)绘制贝塞尔曲线
本文来自CSDN博客,转载请标明出处:http://blog.csdn.net/Fioman/archive/2008/06/23/2578895.aspx
引用:http://www.cs.mtu.edu/~shene/COURSES/cs3621/NOTES/spline/Bezier/de-casteljau.html
德卡斯特里奥算法可以计算贝塞尔曲线上的点C(u),u∈[0,1]。因此,通过给定一组u的值,便可以计算出贝塞尔曲线上的坐标序列,从而绘制出贝塞尔曲线。
德卡斯特里奥算法的基础就是在向量AB上选择一个点C,使得C分向量AB为u:1-u(也就是∣AC∣:∣AB∣= u)。给定点A、B的坐标以及u(u∈[0,1])的值,点C的坐标便为:C = A + (B - A) * u = (1 - u) * A + B * u。
![]()
定义贝塞尔曲线的控制点Pi编号为0i,其中,0表示是第0次迭代。当第一、二、三……次迭代时,0将会被1、2、3……替换。
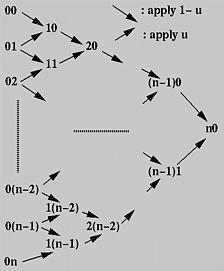
德卡斯特里奥算法的思想如下:为了计算n次贝塞尔曲线上的点C(u), u∈[0,1],首先将控制点连接形成一条折线00-01-02……0(n - 1)-0n。利用上述方法,计算出折线中每条线段0j-0(j+1)上的一个点1j,使得点1j分该线段的比为u:1-u。然后在折线10-11-……-1(n-1)上递归调用该算法,以此类推。最终,求得最后一个点n0。 德卡斯特里奥证明了,点n0一定是曲线上的点。
如上图,曲线控制点是00、01、02、03、04、05。线段00-01上取点10,10分该线段的比为u:1-u,类似地取点11、12、13、14,然后第二次迭代在线段10-11上取点20,点20分该线段的比为u:1-u,类似地取点21、22、23。然后进行下一次迭代,依次类推,直到最后在线段40-41上取点50,50是最终惟一的点,也是在曲线上的点。
上述直观的算法描述可以表达成一个计算方法。
首先,将所有给定的控制点排列成一列,在上图中,即为最左边的一列。每一对相邻的控制点可以伸出两个箭头,分别指向右下方和右上方。在相邻箭头的交叉处,生成一个新的控制点。例如,控制点ij和i(j +1)生成新的控制点(i + 1)j。指向右下方的箭头表示乘以(1 - u),指向右上方的箭头表示乘以u。
因此,通过第0列,可以求出第1列,然后求出第2列……,最终,在n次迭代后,可以到达惟一的一个点n0,这个点就是曲线上的点。
该计算过程算法如下:
Input: array P[0:n] of n+1 points and real number u in [0,1] Output: point on curve, C(u) Working: point array Q[0:n] for i := 0 to n do
Q[i] := P[i]; // save input
for k := 1 to n do
for i := 0 to n - k do
Q[i] := (1 - u)Q[i] + u Q[i + 1];
return Q[0];
该计算方法可以推导出一个递归关系:
但是,直接通过递归方法计算Pi,j效率低下,其原因与通过递归方法计算斐波那契数列一样:递归方法有大量的重复计算。
德卡斯特里奥算法还有一个有趣的性质。对于同一列中的连续的一组控制点,对其应用德卡斯特里奥算法,那么由这些控制点确定的曲线上的点,就是以这组控制点为边的等边三角形中,与这些控制点相对的顶点。
例如:由控制点02、03、04、05确定的曲线上的,对应u的点是32,正如下图中蓝色的等边三角形所表示的。同样,控制点11、12、13确定的曲线上的,对应u的点是31,如图,黄色三角形所示。
根据上面所述,通过给定一组u值,便可以计算出贝塞尔曲线上的坐标序列,从而绘制出贝塞尔曲线。
view plaincopy to clipboardprint? // arrayCoordinate为控制点 void CChildView::DrawBezier(CDC *pDC, const CArray<CPoint, CPoint>& arrayCoordinate) { int n = 0; if((n = arrayCoordinate.GetSize()) < 2) return; double *xarray = new double[n - 1]; double *yarray = new double[n - 1]; double x = arrayCoordinate.GetAt(0).x; double y = arrayCoordinate.GetAt(0).y; for(double t = 0.0; t <=1; t += 0.05 / n) // 调整参数t,计算贝塞尔曲线上的点的坐标,t即为上述u { for(int i = 1; i < n; ++i) { for(int j = 0; j < n - i; ++j) { if(i == 1) // i==1时,第一次迭代,由已知控制点计算 { xarray[j] = arrayCoordinate.GetAt(j).x * (1 - t) + arrayCoordinate[j + 1].x * t; yarray[j] = arrayCoordinate.GetAt(j).y * (1 - t) + arrayCoordinate[j + 1].y * t; continue; } // i != 1时,通过上一次迭代的结果计算 xarray[j] = xarray[j] * (1 - t) + xarray[j + 1] * t; yarray[j] = yarray[j] * (1 - t) + yarray[j + 1] * t; } } pDC->MoveTo(x, y); pDC->LineTo(xarray[0], yarray[0]); x = xarray[0]; y = yarray[0]; } delete [] xarray; delete [] yarray; }
本文来自CSDN博客,转载请标明出处:http://blog.csdn.net/Fioman/archive/2008/06/23/2578895.aspx