十二、Dijkstra算法
戴克斯特拉算法(Dijkstra’s algorithm)是由荷兰计算机科学家艾兹赫尔·戴克斯特拉提出。迪科斯彻算法使用了广度优先搜索解决非负权有向图的单源最短路径问题,算法最终得到一个最短路径树。该算法常用于路由算法或者作为其他图算法的一个子模块。
该算法的输入包含了一个有权重的有向图 G,以及G中的一个来源顶点 S。我们以 V 表示 G 中所有顶点的集合。每一个图中的边,都是两个顶点 所形成的有序元素对。(u, v) 表示从顶点 u 到 v 有路径相连。我们以 E 表示G中所有边的集合,而边的权重则由权重函 数 w: E → [0, ∞] 定义。因此,w(u, v) 就是从顶点 u 到顶点 v 的非负权重(weight)。边的权重可以想像成两个顶点之 间的距离。任两点间路径的权重,就是该路径上所有边的权重总和。已知有 V 中有顶点 s 及 t,Dijkstra 算法可以找到 s 到 t的最低权 重路径(例如,最短路径)。这个算法也可以在一个图中,找到从一个顶点 s 到任何其他顶点的最短路径。对于不含负权的有向图,Dijkstra算法是目 前已知的最快的单源最短路径算法。
算法思想
按路径长度 递增次序产生算法:
把顶点集合V分成两组:
(1)S:已求出的顶点的集合(初始时只含有源点V0)
(2)V-S=T:尚未确定的顶点集合
将T中顶点按递增的次序加入到S中,保证:
(1)从源点V0到S中其他各顶点的长度都不大于从V0到T中任何顶点的最短路径长度
(2)每个顶点对应一个距离值
S中顶点:从V0到此顶点的长度
T中顶点:从V0到此顶点的只包括S中顶点作中间顶点的最短路径长度
依据:可以证明V0到T中顶点Vk的,或是从V0到Vk的直接路径的权值;或是从V0经S中顶点到Vk的路径权值之和
( 反证法可证)
求最短路径步骤
算法步骤如下:
G={V,E}
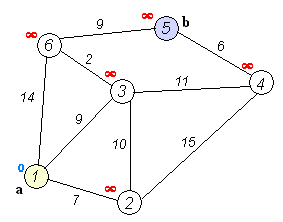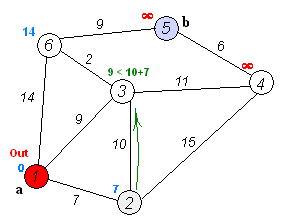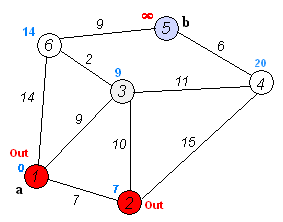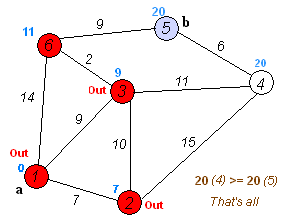
1. 初始时令 S={V0},T=V-S={其余顶点},T中顶点对应的距离值
若存在<V0,Vi>,d(V0,Vi)为<V0,Vi>弧上的权值
若不存在<V0,Vi>,d(V0,Vi)为∞
2. 从T中选取一个与S中顶点有关联边且权值最小的顶点W,加入到S中
3. 对其余T中顶点的距离值进行修改:若加进W作中间顶点,从V0到Vi的距离值缩短,则修改此距离值
重复上述步骤2、3,直到S中包含所有顶点,即W=Vi为止
Dijkstra算法是典型的算法。Dijkstra算法是很有代表性的算法。Dijkstra一般的表述通常有两种方式,一种用永久和临时标号方式,一种是用OPEN, CLOSE表的方式,这里均采用永久和临时标号的方式。注意该算法要求图中不存在负权边。
java语言:
//初始化路径,都为最大值。
int path[][]=new int[n+1][n+1];
for(inti=1;i<n+1;i++){
for(intj=1;j<n+1;j++)
path[i][j]=Integer.MAX_VALUE;
}
//这里需要输入path[i][j]的具体内容,如果有重复数据的话,需要更新路径为最小值。
int minLen[]=new int[n+1];
//visit初始为0,防止回溯
int visit[]=new int[n+1];
//初始化1到其他点的距离。
for(inti=1;i<n+1;i++){
minLen[i]=path[1][i];
}
void Dijkstra(){
minLen[1]=0;
visit[1]=1;
int minj=1;
for(int i=1;i<n+1;i++){
int min=Integer.MAX_VALUE;
for(intj=1;j<n+1;j++){
if(visit[j]==0&&minLen[j]<min){
min=minLen[j];
minj=j;
}
}
visit[minj]=1;
for(int j=1;j<n+1;j++){
if(visit[j]==0&&minLen[minj]!=Integer.MAX_VALUE&&path[minj][j]!=
Integer.MAX_VALUE&&minLen[j]>(minLen[minj]+path[minj][j])){
minLen[j]=minLen[minj]+path[minj][j];
}
}
}
}
C语言
#include<stdio.h>
#include<stdlib.h>
#define max 11000000000
int a[1000][1000];
int d[1000];//d表示某特定边距离
int p[1000];//p表示永久边距离
int i,j,k;
int m;//m代表边数
int n;//n代表点数
int main()
{
scanf("%d%d",&n,&m);
int min1;
int x,y,z;
for(i=1;i<=m;i++)
{
scanf("%d%d%d",&x,&y,&z);
a[x][y]=z;
a[y][x]=z;
}
for(i=1;i<=n;i++)
d[i]=max1;
d[1]=0;
for(i=1;i<=n;i++)
{
min1=max1;
for(j=1;j<=n;j++)
if(!p[j]&&d[j]<min1)
{
min1=d[j];
k=j;
}
p[k]=j;
for(j=1;j<=n;j++)
if(a[k][j]!=0&&!p[j]&&d[j]>d[k]+a[k][j])
d[j]=d[k]+a[k][j];
}
for(i=1;i<n;i++)
printf("%d->",p[i]);
printf("%d\n",p[n]);
return 0;
}