概率分布

概率分布

相关基础知识

贝叶斯定理

  贝叶斯定理也称贝叶斯推理。它用于将先验概率转化为后验概率，也就是我们先知道一件事情发现的概率p（x）（先验概率），然后根据条件概率p（y|x）观察到一定数量的事件y（条件概率），最后再重新估计一下这件事情发生的概率p(x|y)（后验概率）。具体的数学公式如下：

p(x|y)=p(y|x)p(x)∑x′p(y|x′)p(x′)

  我们可以这样理解，一开始没有具体的数据，我们人为去猜想事件x发生的概率是p（x），然后开始做一堆实验，得到一些真实数据y，然后现在有了数据，再去修正一下之前猜想的概率，这样就实现了先验转后验p（x）->p（x|y）。
  举个栗子：现在我想知道一枚硬币正反面朝上的概率是多少，现在还没做实验我们认为正反两面出现的概率分别是 p（正）=35 与 p（反）=25 。好的，现在开始做实验，我们抛10次硬币，结果是8次正面，2次反面，也就是 p(实验正面|正)=45 与 p(实验反面|反)=15 。现在根据贝叶斯定理重新计算一下这枚硬币正反面朝上的概率是多少：

p(正|实验正面)=p(实验正面|正)p(正)p(实验正面|正)p(正)+p(实验反面|正)p(反)=45∗3515∗25+45∗35=1214

  如果是偏频派，就不会关心先验，直接根据实验结果得出 p（正）=45≠1214 。

二项分布与贝塔分布

伯努利分布

  考虑一个二元随机变量 x∈{0,1} ,为了方便理解，我们可以假设 x=1 表示的是硬币正面朝上的概率而 x=0 表示的是硬币反面朝上的概率，其中 x=1 的概率被记作参数 μ ,因此 p(x=1|μ)=μ ，而 p(x=0|μ)=1−μ 。我们可以看到 x 的概率分布可以写成：

Bern(x|μ)=μx(1−μ)(1−x)

这被称为是伯努利分布（Bernoulli distribution），均值和方差分别是 E[x]=μ 与 var[x]=μ（1−μ） 。

二项分布

  接着上面的伯努利分布，如果我们做了 N 次试验全部结果的集合是  且 m 次朝上，且每一次试验都是独立的在 N 次抛掷中，我们把所有 m 朝上的方式都加起来，因此就得到了二项分布(binomial distribution)：

bin(m|N，μ)=(Nm)μm(1−μ)(N−m)

它的期望和方差分别是 E[x]=Nμ 与 var[x]=Nμ（1−μ） 。

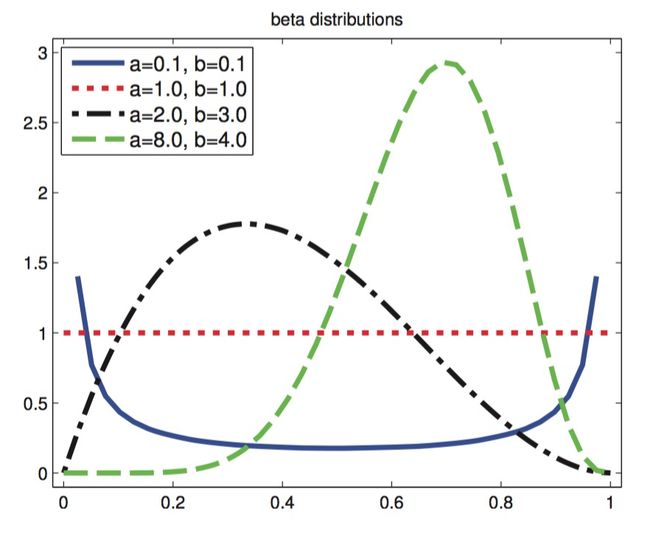
贝塔分布

  根据上面的推导，当给定数据集的情况下，我们就可以根据最大似然估计出 μ 的值是多少，但是对于小规模的数据，会造成严重的过拟合现象（过拟合：在训练数据集上拟合得很好，但是在训练数据集上表现比较差，泛化能力太差）。我们从贝叶斯的观点去看待这个问题，我们可以根据人为的经验（先验）与数据（条件概率）共同来决定参数的值，这样就能防止过拟合，因此参数的值不完全依赖于真实的数据，也就是最终并不会非常好地拟合训练数据，这样能提高算法的泛化能力，进而防止过拟合。对于参数 μ ，我们不再认为它是一个固定的值，而是服从一个分布 p（μ） ，如果我们选择一个正比于 μ 和 1−μ 的幂指数的先验分布，那么后验概率就会有着与先验分布相同的函数形式，这个性质被称为共轭性（conjugacy）。贝塔分布（Beta distribution）满足这样的性质，因此beta分布被称为二项分布的共轭先验，也可以理解为是参数 μ 所服从的一个分布，定义为：

Beta(μ|a,b)=Γ(a+b)Γ(a)Γ(b)μa−1(1−μ)(b−1)

其中参数a与b被称为超参（hyperparameter），可以理解为是参数的参数。 Γ(x) 是伽马（Gamma）函数：

∫∞0ux−1e−udu

且伽马函数很重要的一个性质是 Γ(x+1)=xΓ(x) 。（待会会用到）
  根据贝叶斯定理，我们将Beta先验与二项分布相乘就可以得到参数 μ 的后验概率分布（对于任何参数值，贝叶斯定理的分母都是一个常数，所以我们可以不用理会）

p(μ|N,a,b)∝bin(m|N，μ)×Beta(μ|a,b)=N!Γ(a+b)m!Γ(a)(N−m)!Γ(b)μm+a−1(1−μ)(N−m+b−1)=(a+b−1)!Γ(a+b+N)(a−1)!Γ(a+m)(b−1)!Γ(b+N−m)μm+a−1(1−μ)(N−m+b−1)∝Γ(a+b+N)Γ(a+m)Γ(b+N−m)μm+a−1(1−μ)(N−m+b−1)

我们现在可以发现这仅仅是另一个Beta分布，因此Beta分布可以称为是二项分布的贝叶斯版本。

多项分布与狄利克雷分布

多项分布

  如果我们的变量的取值不止0与1这两种情况，而是可以取得K个不同的值，即 x∈{0,K} ， mk 为出现变量等于k的次数且 ∑Kk=1mk=N 。我们对二项分布进行拓展，就可以得到多项分布(Multivariate distribution)：

Mult（m1,m2,...,mK|μ,N）=(Nm1,m2,...,mK)∏k=1Kμmkk=N!m1!m2!...,mK!∏k=1Kμmkk

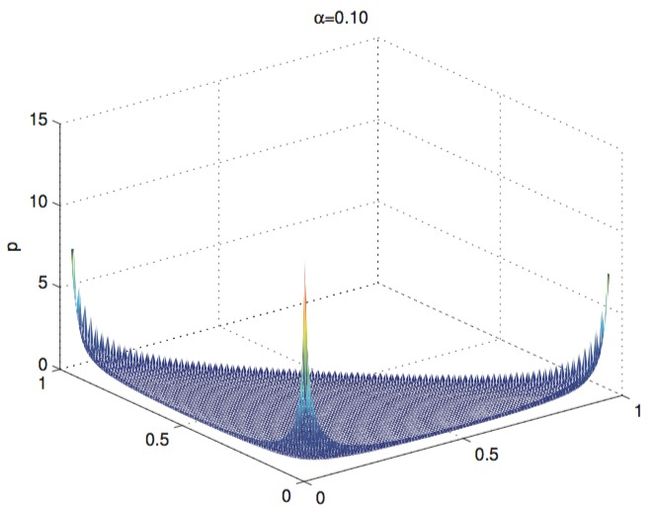
狄利克雷分布

  多项分布对应二项分布，相对应地，狄利克雷分布(Dirichlet distribution)对应着贝塔分布，狄利克雷分布是多项分布的共轭先验，是多项分布的贝叶斯版本。公式为：

Dir(μ→|α→)=Γ(α0)Γ(α0)…Γ(αK)∏k=1Kμαk+mk−1k

其中 α0=∑Kk=1αk 经过贝叶斯推断，先验转后验后，参数 μ 的后验概率是：

p(μ|N,α)∝Mult（m1,m2,...,mK|μ,N）Dir(μ|α)∝Γ(α0+N)Γ(α0+m1)…Γ(αK+mK)∏k=1Kμαk+mk−1k=Dir(μ→|α→+m→)

高斯分布

熵

  变量 x 服从分布 p(x) , 熵 H[x] 是用来衡量变量 x 的不确定性的。熵越大，表示 x 的值越不确定，当变量的分布是均匀分布的时候，熵的值达到最大。

H[x]=−∑xp(x)lnp(x)

当 x 是连续值的时候，讲累加符号换成积分：

H[x]=−∫p(x)lnp(x)dx

高斯分布

  高斯分布（Gaussian distribution）应该是大家最熟悉的分布了，表示的是连续变量的概率分布。

我们从熵中把高斯分布推导出来。变量 x 的分布 p（x） 必须满足如下三个条件：

∫∞−∞p(x)dx=1

∫∞−∞xp(x)dx=μ

∫∞−∞(x−μ)2p(x)dx=σ2

第一个条件保证概率的和为1，其余两个确定概率的期望和方差，若没有后两个限制条件，所求得的概率分布将是均匀的。我们现在确定一个期望，保证分布有一个峰值。以及一个方差，表示变量的离散程度。在满足这三个限制条件的情况下最大化熵所求得的分布就是高斯分布。因此，有一些算法说最大熵xxx算法，其实就是假设算法中的变量或参数服从高斯分布，因为高斯分布是是在确定期望与方差的情况下熵最大的分布，比如最大熵隐马尔可夫就是假设了条件概率服从高斯分布。求解这个熵是凸优化中的带约束的求解问题，可以使用使用拉格朗日乘数法通过求解原问题的对偶问题找到一个近似解。 H[x] 的对偶函数是：

D[x]=−∫∞−∞p(x)lnp(x)dx+λ1(∫∞−∞p(x)dx−1)+λ2(∫∞−∞xp(x)dx−μ)+λ3(∫∞−∞(x−μ)2p(x)dx−σ2)

我们使用变分法求解上面的泛函，我们现在假设 p(x)=p(x)+ϵη(x) ，因此：
我们可以得到：

D[x+ϵη(x)]=−∫∞−∞p(x)lnp(x)dx−ϵ{∫∞−∞η(x)lnp(x)dx+∫∞−∞p(x)1p(x)η(x)dx}+λ1(∫∞−∞p(x)dx+ϵ∫∞−∞η(x)dx−1)+λ2(∫∞−∞xp(x)dx−μ+ϵ∫∞−∞xη(x)dx)+λ3(∫∞−∞(x−μ)2p(x)dx−σ2+ϵ∫∞−∞(x−μ)2η(x)dx)

根据:

D[x+ϵη(x)]=D[x]+ϵ∫dDdp(x)η(x)dx+O(ϵ2)

我们可以得到（位对应）：

dDdp(x)=−lnp(x)−1+λ1+λ2x+λ3(x−μ)2=0

p(x)=exp(−1+λ1+λ2x+λ3(x−μ)2)

代入三个约束条件后可以得到：

λ1=1−12ln(2πσ2)λ2=0λ3=12σ2

最终结果是高斯分布：

(x|μ,σ2)=12πσ2‾‾‾‾‾√exp{−12σ2(x−μ)2}

泊松分布

  泊松分布（Possion distribution）是最重要的离散分布之一，经常用于表示随机变量x在一定时间或空间内出现时间的次数。和二项分布不同的是，泊松分布适合实验次数多且时间发生的概率很低的情况，比如某段时间路口发生交通事故次数的概率，但泊松分布可以通过二项分布推出，我们先设二项分布：

p(X=k)=(nk)pk(1−p)n−k

limn→∞p(X=k)=limn→∞(nk)pk(1−p)n−k=limn→∞n!(n−k)!k!(λn)k(1−λn)n−k=limn→∞n!nk(n−k)!(λkk!)(1−λn)n(1−λn)−k=limn→∞[(1−1n)(1−2n)...(1−k−1n)](λkk!)(1−λn)n(1−λn)−k=(λkk!)exp(−λ)=poi(λ)

泊松分布可以近似地看成是离散变量的高斯分布，且均值和方差都是 λ 。

拉普拉斯分布

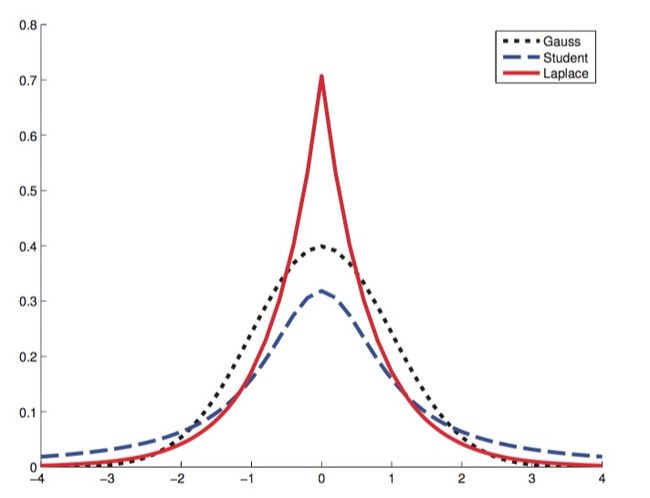
  拉普拉斯分布（Laplace distribution）是一个有长尾的分布，和高斯分布有点像，只是峰值更尖且尾更长。

Lap(x|μ,b)=12bexp(−−|x−μ|b)

其中，它的期望和方差分别是 μ 与 2b2 。

学生t分布

  高斯分布与拉普拉斯分布都容易受到奇异点的影响，学生t分布（Student’s t distribution）拥有比它们更好的鲁棒性。

τ(x|μ,σ2,υ)∝[1+1υ(x−μσ)2]−(υ+12)

其中，它的期望和方差分别是 μ 与 υσ2(υ−2) 。