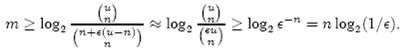bloom filter

今天偶然在微博上看到一篇布隆过滤器的算法，感觉很好玩。决定拿自己宝贵的上午时间学一学。

以前见到的都是用时间换空间或者用空间换时间，而bloom filter则是牺牲正确率换取效率。第一次听说还可以这样玩~~~好兴奋~~~

当然自己是没有那么有才了，先看懂了别人的博客，让我整合一下转化为私有的吧~~（恶呵呵~~）

导读：布隆过滤器（Bloom Filter）是1970年由布隆提出。实际上是一个很长的二进制向量和一系列随机映射函数。用于检索一个元素是否在一个集合中。优点是空间效率和查询时间都远远超过一般的算法，缺点是有一定的误识别率和删除困难。

Bloom Filter是一种空间效率很高的随机数据结构，它利用位数组很简洁地表示一个集合，并能判断一个元素是否属于这个集合。

Bloom Filter的这种高效是有一定代价的：在判断一个元素是否属于某个集合时，有可能会把不属于这个集合的元素误认为属于这个集合（false positive）。

因此，Bloom Filter不适合那些“零错误”的应用场合。而在能容忍低错误率的应用场合下，Bloom Filter通过极少的错误换取了存储空间的极大节省。

集合表示和元素查询

下面我们具体来看Bloom Filter是如何用位数组表示集合的。初始状态时，Bloom Filter是一个包含m位的位数组，每一位都置为0。

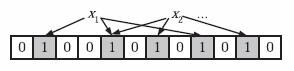
为了表达S={x1, x2,…,xn}这样一个n个元素的集合，Bloom Filter使用k个相互独立的哈希函数（Hash Function），它们分别将集合中的每个元素映射到{1,…,m}的范围中。对任意一个元素x，第i个哈希函数映射的位置hi(x)就会被置为1（1≤i≤k）。注意，如果一个位置多次被置为1，那么只有第一次会起作用，后面几次将没有任何效果。在下图中，k=3，且有两个哈希函数选中同一个位置（从左边数第五位）。

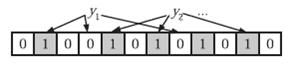
在判断y是否属于这个集合时，我们对y应用k次哈希函数，如果所有hi(y)的位置都是1（1≤i≤k），那么我们就认为y是集合中的元素，否则就认为y不是集合中的元素。下图中y1就不是集合中的元素。y2或者属于这个集合，或者刚好是一个false positive。

错误率估计

前面我们已经提到了，Bloom Filter在判断一个元素是否属于它表示的集合时会有一定的错误率（false positive rate），下面我们就来估计错误率的大小。在估计之前为了简化模型，我们假设kn<m且各个哈希函数是完全随机的。当集合S={x1, x2,…,xn}的所有元素都被k个哈希函数映射到m位的位数组中时，这个位数组中某一位还是0的概率是：

其中1/m表示任意一个哈希函数选中这一位的概率（前提是哈希函数是完全随机的），(1-1/m)表示哈希一次没有选中这一位的概率。要把S完全映射到位数组中，需要做kn次哈希。某一位还是0意味着kn次哈希都没有选中它，因此这个概率就是（1-1/m）的kn次方。令p = e-kn/m是为了简化运算，这里用到了计算e时常用的近似：

令ρ为位数组中0的比例，则ρ的数学期望E(ρ)= p’。在ρ已知的情况下，要求的错误率（false positive rate）为：

(1-ρ)为位数组中1的比例，(1-ρ)k就表示k次哈希都刚好选中1的区域，即false positive rate。上式中第二步近似在前面已经提到了，现在来看第一步近似。p’只是ρ的数学期望，在实际中ρ的值有可能偏离它的数学期望值。M. Mitzenmacher已经证明[2] ，位数组中0的比例非常集中地分布在它的数学期望值的附近。因此，第一步的近似得以成立。分别将p和p’代入上式中，得：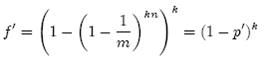

相比p’和f’，使用p和f通常在分析中更为方便。

最优的哈希函数个数

既然Bloom Filter要靠多个哈希函数将集合映射到位数组中，那么应该选择几个哈希函数才能使元素查询时的错误率降到最低呢？这里有两个互斥的理由：如果哈希函数的个数多，那么在对一个不属于集合的元素进行查询时得到0的概率就大；但另一方面，如果哈希函数的个数少，那么位数组中的0就多。为了得到最优的哈希函数个数，我们需要根据上一小节中的错误率公式进行计算。

先用p和f进行计算。注意到f = exp(k ln(1 − e−kn/m))，我们令g = k ln(1 − e−kn/m)，只要让g取到最小，f自然也取到最小。由于p = e-kn/m，我们可以将g写成

根据对称性法则可以很容易看出当p = 1/2，也就是k = ln2· (m/n)时，g取得最小值。在这种情况下，最小错误率f等于(1/2)k ≈ (0.6185)m/n。另外，注意到p是位数组中某一位仍是0的概率，所以p = 1/2对应着位数组中0和1各一半。换句话说，要想保持错误率低，最好让位数组有一半还空着。

需要强调的一点是，p = 1/2时错误率最小这个结果并不依赖于近似值p和f。同样对于f’ = exp(k ln(1 − (1 − 1/m)kn))，g’ = k ln(1 − (1 − 1/m)kn)，p’ = (1 − 1/m)kn，我们可以将g’写成

同样根据对称性法则可以得到当p’ = 1/2时，g’取得最小值。

位数组的大小

下面我们来看看，在不超过一定错误率的情况下，Bloom Filter至少需要多少位才能表示全集中任意n个元素的集合。假设全集中共有u个元素，允许的最大错误率为є，下面我们来求位数组的位数m。

假设X为全集中任取n个元素的集合，F(X)是表示X的位数组。那么对于集合X中任意一个元素x，在s = F(X)中查询x都能得到肯定的结果，即s能够接受x。显然，由于Bloom Filter引入了错误，s能够接受的不仅仅是X中的元素，它还能够є (u - n)个false positive。因此，对于一个确定的位数组来说，它能够接受总共n + є (u - n)个元素。在n + є (u - n)个元素中，s真正表示的只有其中n个，所以一个确定的位数组可以表示

个集合。m位的位数组共有2m个不同的组合，进而可以推出，m位的位数组可以表示

个集合。全集中n个元素的集合总共有

个，因此要让m位的位数组能够表示所有n个元素的集合，必须有

即：

上式中的近似前提是n和єu相比很小，这也是实际情况中常常发生的。根据上式，我们得出结论：在错误率不大于є的情况下，m至少要等于n log2(1/є)才能表示任意n个元素的集合。

上一小节中我们曾算出当k = ln2· (m/n)时错误率f最小，这时f = (1/2)k = (1/2)mln2 / n。现在令f≤є，可以推出

这个结果比前面我们算得的下界n log2(1/є)大了log2 e ≈ 1.44倍。这说明在哈希函数的个数取到最优时，要让错误率不超过є，m至少需要取到最小值的1.44倍。

、 扩展 CounterBloom Filter

CounterBloom Filter

BloomFilter有个缺点，就是不支持删除操作，因为它不知道某一个位从属于哪些向量。那我们可以给Bloom Filter加上计数器，添加时增加计数器，删除时减少计数器。

但这样的Filter需要考虑附加的计数器大小，假如同个元素多次插入的话，计数器位数较少的情况下，就会出现溢出问题。如果对计数器设置上限值的话，会导致Cache Miss，但对某些应用来说，这并不是什么问题，如Web Sharing。

Compressed Bloom Filter

为了能在服务器之间更快地通过网络传输Bloom Filter，我们有方法能在已完成Bloom Filter之后，得到一些实际参数的情况下进行压缩。

将元素全部添加入Bloom Filter后，我们能得到真实的空间使用率，用这个值代入公式计算出一个比m小的值，重新构造Bloom Filter，对原先的哈希值进行求余处理，在误判率不变的情况下，使得其内存大小更合适。

4、 Bloom-Filter的应用

        Bloom-Filter一般用于在大数据量的集合中判定某元素是否存在。例如邮件服务器中的垃圾邮件过滤器。在搜索引擎领域，Bloom-Filter最常用于网络蜘蛛(Spider)的URL过滤，网络蜘蛛通常有一个URL列表，保存着将要下载和已经下载的网页的URL，网络蜘蛛下载了一个网页，从网页中提取到新的URL后，需要判断该URL是否已经存在于列表中。此时，Bloom-Filter算法是最好的选择。

1.key-value 加快查询

       一般Bloom-Filter可以与一些key-value的数据库一起使用，来加快查询。

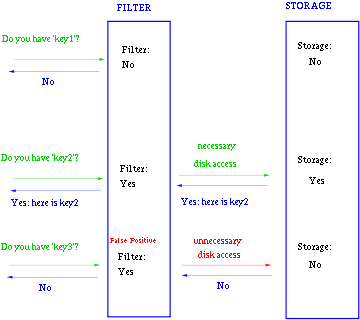
       一般key-value存储系统的values存在硬盘，查询就是件费时的事。将Storage的数据都插入Filter，在Filter中查询都不存在时，那就不需要去Storage查询了。当False Position出现时，只是会导致一次多余的Storage查询。

       由于Bloom-Filter所用的空间非常小，所有BF可以常驻内存。这样子的话，对于大部分不存在的元素，我们只需要访问内存中的Bloom-Filter就可以判断出来了，只有一小部分，我们需要访问在硬盘上的key-value数据库。从而大大地提高了效率。如图：

          

2 .Google的BigTable

        Google的BigTable也使用了Bloom Filter，以减少不存在的行或列在磁盘上的查询，大大提高了数据库的查询操作的性能。

3. Proxy-Cache

      在Internet Cache Protocol中的Proxy-Cache很多都是使用Bloom Filter存储URLs，除了高效的查询外，还能很方便得传输交换Cache信息。

4.网络应用

      1）P2P网络中查找资源操作，可以对每条网络通路保存Bloom Filter，当命中时，则选择该通路访问。

      2）广播消息时，可以检测某个IP是否已发包。

      3）检测广播消息包的环路，将Bloom Filter保存在包里，每个节点将自己添加入Bloom Filter。

     4）信息队列管理，使用Counter Bloom Filter管理信息流量。

5. 垃圾邮件地址过滤

        像网易，QQ这样的公众电子邮件（email）提供商，总是需要过滤来自发送垃圾邮件的人（spamer）的垃圾邮件。

一个办法就是记录下那些发垃圾邮件的 email地址。由于那些发送者不停地在注册新的地址，全世界少说也有几十亿个发垃圾邮件的地址，将他们都存起来则需要大量的网络服务器。

如果用哈希表，每存储一亿个 email地址，就需要 1.6GB的内存（用哈希表实现的具体办法是将每一个 email地址对应成一个八字节的信息指纹，然后将这些信息指纹存入哈希表，由于哈希表的存储效率一般只有 50%，因此一个email地址需要占用十六个字节。一亿个地址大约要 1.6GB，即十六亿字节的内存）。因此存贮几十亿个邮件地址可能需要上百 GB的内存。

而Bloom Filter只需要哈希表 1/8到 1/4 的大小就能解决同样的问题。

BloomFilter决不会漏掉任何一个在黑名单中的可疑地址。而至于误判问题，常见的补救办法是在建立一个小的白名单，存储那些可能别误判的邮件地址。

5、 Bloom-Filter的具体实现

c语言实现：

stdafx.h：

 #pragma once
 #include <stdio.h>
 #include "stdlib.h"
 #include <iostream>
 #include <time.h>
 using namespace std;

 #include "stdafx.h"


 #define ARRAY_SIZE 256 /*we get the 256 chars of each line*/
 #define SIZE 48000000 /* size should be 1/8 of max*/
 #define MAX  384000000/*the max bit space*/

 #define SETBIT(ch,n) ch[n/8]|=1<<(7-n%8)
 #define GETBIT(ch,n) (ch[n/8]&1<<(7-n%8))>>(7-n%8)

 unsigned int len(char *ch);/* functions to calculate the length of the url*/

 unsigned int RSHash(char* str, unsigned int len);/* functions to calculate the hash value of the url*/
 unsigned int JSHash(char* str, unsigned int len);/* functions to calculate the hash value of the url*/
 unsigned int PJWHash(char* str, unsigned int len);/* functions to calculate the hash value of the url*/
 unsigned int ELFHash(char* str, unsigned int len);/* functions to calculate the hash value of the url*/
 unsigned int BKDRHash(char* str, unsigned int len);/* functions to calculate the hash value of the url*/
 unsigned int SDBMHash(char* str, unsigned int len);/* functions to calculate the hash value of the url*/
 unsigned int DJBHash(char* str, unsigned int len);/* functions to calculate the hash value of the url*/
 unsigned int DEKHash(char* str, unsigned int len);/* functions to calculate the hash value of the url*/
 unsigned int BPHash(char* str, unsigned int len);/* functions to calculate the hash value of the url*/
 unsigned int FNVHash(char* str, unsigned int len);/* functions to calculate the hash value of the url*/
 unsigned int APHash(char* str, unsigned int len);/* functions to calculate the hash value of the url*/
 unsigned int HFLPHash(char* str,unsigned int len);/* functions to calculate the hash value of the url*/
 unsigned int HFHash(char* str,unsigned int len);/* functions to calculate the hash value of the url*/
 unsigned int StrHash( char* str,unsigned int len);/* functions to calculate the hash value of the url*/
 unsigned int TianlHash(char* str,unsigned int len);/* functions to calculate the hash value of the url*/


 int main()
 {
     int i,num,num2=0; /* the number to record the repeated urls and the total of it*/
     unsigned int tt=0;
     int flag;         /*it helps to check weather the url has already existed */
     char buf[257];    /*it helps to print the start time of the program */
     time_t tmp = time(NULL);

     char file1[100],file2[100];
     FILE *fp1,*fp2;/*pointer to the file */
     char ch[ARRAY_SIZE];
     char *vector ;/* the bit space*/
     vector = (char *)calloc(SIZE,sizeof(char));

     printf("Please enter the file with repeated urls:\n");
     scanf("%s",&file1);
     if( (fp1 = fopen(file1,"rb")) == NULL) {  /* open the goal file*/
       printf("Connot open the file %s!\n",file1);
     }

     printf("Please enter the file you want to save to:\n");
     scanf("%s",&file2);
     if( (fp2 = fopen(file2,"w")) == NULL) {
         printf("Connot open the file %s\n",file2);
     }
     strftime(buf,32,"%Y-%m-%d %H:%M:%S",localtime(&tmp));
     printf("%s\n",buf); /*print the system time*/

     for(i=0;i<SIZE;i++) {
         vector[i]=0;  /*set 0*/
     }

     while(!feof(fp1)) { /* the check process*/

         fgets(ch,ARRAY_SIZE,fp1);
         flag=0;
         tt++;
         if( GETBIT(vector, HFLPHash(ch,len(ch))%MAX) ) {
             flag++;
         } else {
             SETBIT(vector,HFLPHash(ch,len(ch))%MAX );
         }

         if( GETBIT(vector, StrHash(ch,len(ch))%MAX) ) {
             flag++;
         } else {
             SETBIT(vector,StrHash(ch,len(ch))%MAX );
         }

         if( GETBIT(vector, HFHash(ch,len(ch))%MAX) )   {
             flag++;
         } else {
             SETBIT(vector,HFHash(ch,len(ch))%MAX );
         }

         if( GETBIT(vector, DEKHash(ch,len(ch))%MAX) ) {
             flag++;
         } else {
             SETBIT(vector,DEKHash(ch,len(ch))%MAX );
         }

         if( GETBIT(vector, TianlHash(ch,len(ch))%MAX) ) {
             flag++;
         } else {
             SETBIT(vector,TianlHash(ch,len(ch))%MAX );
         }

         if( GETBIT(vector, SDBMHash(ch,len(ch))%MAX) )  {
             flag++;
         } else {
             SETBIT(vector,SDBMHash(ch,len(ch))%MAX );
         }

         if(flag<6)
             num2++;
         else
            fputs(ch,fp2);

         /*  printf(" %d",flag); */
     }
     /* the result*/
     printf("\nThere are %d urls!\n",tt);
     printf("\nThere are %d not repeated urls!\n",num2);
     printf("There are %d repeated urls!\n",tt-num2);
     fclose(fp1);
     fclose(fp2);
     return 0;
 }


 /*functions may be used in the main */
 unsigned int len(char *ch)
 {
     int m=0;
     while(ch[m]!='\0') {
         m++;
     }
     return m;
 }

 unsigned int RSHash(char* str, unsigned int len) {
    unsigned int b = 378551;
    unsigned int a = 63689;
    unsigned int hash = 0;
    unsigned int i = 0;

    for(i=0; i<len; str++, i++) {
       hash = hash*a + (*str);
       a = a*b;
    }
    return hash;
 }
 /* End Of RS Hash Function */


 unsigned int JSHash(char* str, unsigned int len)
 {
    unsigned int hash = 1315423911;
    unsigned int i    = 0;

    for(i=0; i<len; str++, i++) {
       hash ^= ((hash<<5) + (*str) + (hash>>2));
    }
    return hash;
 }
 /* End Of JS Hash Function */


 unsigned int PJWHash(char* str, unsigned int len)
 {
    const unsigned int BitsInUnsignedInt = (unsigned int)(sizeof(unsigned int) * 8);
    const unsigned int ThreeQuarters = (unsigned int)((BitsInUnsignedInt  * 3) / 4);
    const unsigned int OneEighth = (unsigned int)(BitsInUnsignedInt / 8);
    const unsigned int HighBits = (unsigned int)(0xFFFFFFFF) << (BitsInUnsignedInt - OneEighth);
    unsigned int hash = 0;
    unsigned int test = 0;
    unsigned int i = 0;

    for(i=0;i<len; str++, i++) {
       hash = (hash<<OneEighth) + (*str);
       if((test = hash & HighBits)  != 0) {
          hash = ((hash ^(test >> ThreeQuarters)) & (~HighBits));
       }
    }

    return hash;
 }
 /* End Of  P. J. Weinberger Hash Function */


 unsigned int ELFHash(char* str, unsigned int len)
 {
    unsigned int hash = 0;
    unsigned int x    = 0;
    unsigned int i    = 0;

    for(i = 0; i < len; str++, i++) {
       hash = (hash << 4) + (*str);
       if((x = hash & 0xF0000000L) != 0) {
          hash ^= (x >> 24);
       }
       hash &= ~x;
    }
    return hash;
 }
 /* End Of ELF Hash Function */


 unsigned int BKDRHash(char* str, unsigned int len)
 {
    unsigned int seed = 131; /* 31 131 1313 13131 131313 etc.. */
    unsigned int hash = 0;
    unsigned int i    = 0;

    for(i = 0; i < len; str++, i++)
    {
       hash = (hash * seed) + (*str);
    }

    return hash;
 }
 /* End Of BKDR Hash Function */


 unsigned int SDBMHash(char* str, unsigned int len)
 {
    unsigned int hash = 0;
    unsigned int i    = 0;

    for(i = 0; i < len; str++, i++) {
       hash = (*str) + (hash << 6) + (hash << 16) - hash;
    }

    return hash;
 }
 /* End Of SDBM Hash Function */


 unsigned int DJBHash(char* str, unsigned int len)
 {
    unsigned int hash = 5381;
    unsigned int i    = 0;

    for(i = 0; i < len; str++, i++) {
       hash = ((hash << 5) + hash) + (*str);
    }

    return hash;
 }
 /* End Of DJB Hash Function */


 unsigned int DEKHash(char* str, unsigned int len)
 {
    unsigned int hash = len;
    unsigned int i    = 0;

    for(i = 0; i < len; str++, i++) {
       hash = ((hash << 5) ^ (hash >> 27)) ^ (*str);
    }
    return hash;
 }
 /* End Of DEK Hash Function */


 unsigned int BPHash(char* str, unsigned int len)
 {
    unsigned int hash = 0;
    unsigned int i    = 0;
    for(i = 0; i < len; str++, i++) {
       hash = hash << 7 ^ (*str);
    }

    return hash;
 }
 /* End Of BP Hash Function */


 unsigned int FNVHash(char* str, unsigned int len)
 {
    const unsigned int fnv_prime = 0x811C9DC5;
    unsigned int hash      = 0;
    unsigned int i         = 0;

    for(i = 0; i < len; str++, i++) {
       hash *= fnv_prime;
       hash ^= (*str);
    }

    return hash;
 }
 /* End Of FNV Hash Function */


 unsigned int APHash(char* str, unsigned int len)
 {
    unsigned int hash = 0xAAAAAAAA;
    unsigned int i    = 0;

    for(i = 0; i < len; str++, i++) {
       hash ^= ((i & 1) == 0) ? (  (hash <<  7) ^ (*str) * (hash >> 3)) :
                                (~((hash << 11) + (*str) ^ (hash >> 5)));
    }

    return hash;
 }
 /* End Of AP Hash Function */
 unsigned int HFLPHash(char *str,unsigned int len)
 {
    unsigned int n=0;
    int i;
    char* b=(char *)&n;
    for(i=0;i<strlen(str);++i) {
      b[i%4]^=str[i];
     }
     return n%len;
 }
 /* End Of HFLP Hash Function*/
 unsigned int HFHash(char* str,unsigned int len)
 {
    int result=0;
    char* ptr=str;
    int c;
    int i=0;
    for (i=1;c=*ptr++;i++)
    result += c*3*i;
    if (result<0)
       result = -result;
    return result%len;
 }
 /*End Of HKHash Function */

  unsigned int StrHash( char *str,unsigned int len)
  {
     register unsigned int   h;
     register unsigned char *p;
      for(h=0,p=(unsigned char *)str;*p;p++) {
          h=31*h+*p;
      }

       return h;

   }
  /*End Of StrHash Function*/

 unsigned int TianlHash(char *str,unsigned int len)
 {
    unsigned long urlHashValue=0;
    int ilength=strlen(str);
    int i;
    unsigned char ucChar;
    if(!ilength)  {
        return 0;
    }
    if(ilength<=256)  {
       urlHashValue=16777216*(ilength-1);
   } else {
       urlHashValue = 42781900080;
   }
   if(ilength<=96) {
       for(i=1;i<=ilength;i++) {
           ucChar=str[i-1];
           if(ucChar<='Z'&&ucChar>='A')  {
               ucChar=ucChar+32;
           }
           urlHashValue+=(3*i*ucChar*ucChar+5*i*ucChar+7*i+11*ucChar)%1677216;
       }
   } else  {
       for(i=1;i<=96;i++)
       {
           ucChar=str[i+ilength-96-1];
           if(ucChar<='Z'&&ucChar>='A')
           {
               ucChar=ucChar+32;
           }
           urlHashValue+=(3*i*ucChar*ucChar+5*i*ucChar+7*i+11*ucChar)%1677216;
       }
   }
   return urlHashValue;

  }
 /*End Of Tianl Hash Function*/

全部都是网上找的。