- API接口设计模板
Annaday
java
API员工登录接口设计基本信息Path:/admin/staff/login**Method:**POST接口描述:请求参数Query参数名称是否必须示例备注username是admin用户名password是mima密码返回数据名称类型是否必须默认值备注其他信息codeinteger必须dataString必须data_idLong必须data_usernameString必须data_phon
- 51单片机——串口向电脑发送数据
Uitwaaien54
51单片机嵌入式硬件单片机
引言在电子技术领域,51单片机作为一种广泛应用的微控制器,其串口通信功能具有重要意义。通过串口,51单片机能够与电脑等外部设备进行数据交互,实现各种复杂的功能,为许多应用场景提供了可能。51单片机串口通信基础通信接口概述:常见的通信接口有UART、IIC、SPI等。UART串口通信是51单片机常用的通信方式之一,具有全双工、异步的特点,可实现点对点通信。串口工作原理:在51单片机中,串口通过TXD
- Python Connect OracleDB
ddttoop
Python3WorkTools
Python连接Oracle数据库原文链接:https://blog.csdn.net/xinyuzxx/article/details/81703625cx_Oraclecx_Oracle模块是Python连接Oracle数据库的模块,在Python中,如果要连接Oracle,必须先安装cx_Oracle模块。cx_Oracle的下载地址:https://pypi.python.org/pypi
- python打包opencv为exe可执行程序
AIOT魔法师
YOLOv5和YOLOv11opencvpython计算机视觉
网上很多教程但是呢,每次运行起来打包出来的exe,都会报错,多数是提示找不到cv2的库,或者说让安装opencv,例如下面这种:解决方案如下:1、使用opencv-python的版本为:pipinstall-ihttps://pypi.douban.com/simple/opencv-python==4.3.0</
- kubernetes 安装 kubernetes-dashboard 7.x
kubernetes安装kubernetes-dashboard7.x介绍Kubernetes仪表板是Kubernetes集群的通用、基于Web的UI。它允许用户管理集群中运行的应用程序并对其进行故障排除,以及管理集群本身。从7.x版开始,不再支持基于Manifest的安装。现在只支持基于Helm的安装。由于多容器设置和对Kong网关API代理的严重依赖要轻松支持基于清单安装是不可行的。安装#添加
- Python 安装库报错 “python setup.py egg_info did not run successfully.“
SmallerFL
其他问题fixMac环境设置安装Python相关python开发语言人工智能nlp
文章目录1.Python安装库报错2.问题解决3.参考1.Python安装库报错有时Python用pipinstall安装库的时候会报错,pythonsetup.pyegg_infodidnotrunsuccessfully.,我在安装deepspeed报错示例如下:Preparingmetadata(setup.py)...errorerror:subprocess-exited-with-er
- 一文读懂:AI 工具 Cursor、DeepSeek 和 Copilot 的区别与使用方法
AI云极
【AI智能系列】人工智能copilot
在人工智能技术迅猛发展的今天,各类AI工具层出不穷,为编程、搜索、写作等领域带来了极大的便利。今天,我们将深入介绍三款备受瞩目的AI工具:Cursor、DeepSeek和Copilot。它们各有特色,适合不同场景。想知道它们之间有哪些区别?又该如何使用?一起往下看!一、什么是Cursor、DeepSeek和Copilot?1.CursorCursor是一款专为程序员打造的智能代码编辑工具,结合AI
- Qwen1.5:使用VLLM加速推理模型(包含:OpenAI如何调用)
写bug如流水
大模型vllmQwen1.5openAI
如何安装和配置VLLM库在开始使用VLLM库之前,首先需要确保安装正确的版本。以下指南将帮助你完成安装和配置。安装VLLM库根据你的需求选择合适的版本进行安装。如果你只需要基本功能,可以安装版本0.3。使用以下命令安装:pipinstallvllm==0.3如果你需要使用GPTQ-int8量化模型,那么应该安装0.4或更高版本:pipinstallvllm>=0.4启动模型服务在安装完毕后,可以通
- ML.NET速览
aixing8475
人工智能操作系统runtime
什么是ML.NET?ML.NET是由微软创建,为.NET开发者准备的开源机器学习框架。它是跨平台的,可以在macOS,Linux及Windows上运行。机器学习管道ML.NET通过管道(pipeline)方式组合机器学习过程。整个管道分为以下四个部分:LoadData加载数据TransformData转换数据ChooseAlgorithm选择算法TrainModel训练模型示例建立一个控制台项目。
- pip 安装 numpy 报错 AttributeError: module ‘pkgutil‘ has no attribute ‘ImpImporter‘
小郎碎碎念
我恨BUGLinux运维pipnumpypython
conda环境下pip安装numpy1.x版本,报如下错误File"C:\Users\UserName\AppData\Local\Temp\pip-build-env-_lgbq70y\overlay\Lib\site-packages\pkg_resources\__init__.py",line2191,inregister_finder(pkgutil.ImpImporter,find_o
- Ubuntu安装docker
张3蜂
软件安装部署开源linuxubuntudockereureka
snapinstalldocker#version27.2.0,oraptinstallpodman-docker#version3.4.4+ds1-1ubuntu1.22.04.2aptinstalldocker.io#version24.0.7-0ubuntu2~22.04.1我应该安装哪一个,部署企业级应用?在部署企业级应用时,选择合适的容器化工具非常重要。以下是针对你提到的三种选项的分析和
- 在高分辨率或者扩展屏下微信截图出现放大问题的解决
张3蜂
eclipse
一般这种情况是在电脑的分辨率过高或者采用扩展屏时候出现。解决办法如下:右键微信快捷图标或者可执行程序,属性-兼容性-更改高DPI设置-勾选替代高DPI缩放行为,然后下面选择应用程序就好了。这个在部分软件的界面字体缩小很厉害、界面变下的软件,就得勾选替代高DPI缩放行为--选择系统增强等。所有的截图软件,当开启扩展屏,截图功能无法正常使用时,都可以采用此方法解决问题。
- python 开发app
三希
python开发语言
在Python中开发应用程序(通常指的是移动应用)有多种方法。以下是两种常见的技术栈:KivyKivy是一个开源Python库,用于快速开发跨平台的触控应用。它支持Android、iOS、Windows、MacOS和Linux。以下是使用Kivy开发的基本步骤:1.安装Kivy:在命令行中使用pip安装Kivy:pipinstallkivy2.创建你的应用:创建一个简单的Python文件,比如ma
- selenium 获取token
test明成长记
selenuim+pythonseleniumpython
在不用(或不知道接口)接口获取token的情况下,通过selenium登录获取到token------该token值会作为后续调用接口的凭证ps:token、cookie都可以是接口中需要的凭证(别的遇到了再说),具体看项目中是如何应用的。首先可以通过F12的方式,用postman测试哪一些凭证是必须的,然后想办法拿到他今天遇到的是token刚开始一直掉在下面这个坑里面,需要的就是这个X-API-
- 【使用PyQt创建美观和功能丰富界面】
Dreams°123
pyqtmicrosoftpython
使用PyQt创建美观和功能丰富界面-适用于APP一、基本概念与环境搭建二、布局管理三、部件使用与定制四、信号与槽机制深入应用五、样式表(stylesheet)和主题应用一、基本概念与环境搭建安装PyQt使用以下命令安装PyQt:pipinstallPyQt5(如果使用Python3)。理解信号与槽机制信号(Signal):是对象发出的事件通知,例如按钮的点击、文本框内容的改变等。槽(Slot):是
- Rocky9.5编译freeswitch1.10.12
狂爱代码的码农
VOIP那些事freeswitch
nmtuirebootrm-rf*tarxvfzfreeswitch-1.10.12.-release.tar.gzmvfreeswitch-1.10.12.-releasefreeswitchlscdfreeswitchlsdnfinstallepel-release-ydnfupdate-ydnfgroupinstall"DevelopmentTools"-ylsdnfinstallyasm-
- GCC编译过程,静态库与动态库
南菠湾
开发语言c语言
一、Linux下GCC编译器编译过程序号过程名过程代码1预处理preprocessing将.c中的头文件,宏定义展开及替换,生成.i文件gcc-E-ohello.ihello.c2编译compilation将预处理之后的.i文件生成汇编代码.s文件gcc-S-ohello.shello.i3汇编assembly把.s汇编文件生成.o目标文件gcc-c-ohello.ohello.s4链接linki
- Centos安装python3详细教程
Circle square
自学pythoncentoslinux
文章目录Centos安装python3详细教程1、先查看系统python的位置在哪儿2、下载python3的包之前,要先安装相关的依赖包,用于下载编译python3:3、默认的centos7是没有安装pip,先添加epel扩展源4、安装pip5、用pip装wget6、用wget下载python3的源码包,或者自己先下载好,上传到服务器再安装,如果网络快可以直接安装7、编译python3源码包,解压
- nvdia triton server运行pt文件
滑稽的柴犬
神经网络机器学习python
tritonserver默认都是tensorrt推理。但也会出现有操作不支持,导致无法转模型为engine的情况。可以选择直接运行pytorch的pt文件,以下为操作步骤。1.pytorch后端环境编译步骤原理是使用pytorchC++API运行pt文件模型。安装依赖项apt-getinstallpatchelfrapidjson-devpython3-dev构建NGC的PyTorch容器。例如,
- 【Validator】字段验证器介绍,及基本使用go案例
{⌐■_■}
golang开发语言后端
Go语言Validator字段验证详解validator是Go语言中非常流行的一个字段验证库,支持多种数据类型的验证规则,非常适合用于表单校验、API输入参数校验等场景。安装Validatorgogetgithub.com/go-playground/validator/v101.初始化Validator在使用validator前,需要对验证器进行初始化。import("github.com/go
- 周报(2025.1.20 ~ 2025.1.26)
@Happiness.
cocoamacosobjective-c
一、CodeforcesRound998(Div.3)E题用到并查集并查集模板#includeusingnamespacestd;#definelllonglong#definePIIpair#defineendl'\n'structDSU{vectorf,siz;DSU(){}DSU(lln){init(n);}voidinit(lln){f.resize(n);iota(f.begin(),f
- ElasticSearch 8以及ElasticSearch 7.17以上 推荐使用ElasticSearch Java API,ElasticSearch高级组合检索
朱杰jjj
elasticsearchjava大数据
前言最近在测试使用ElasticSearch7.17遇到了一些使用问题弃用了HighLevelRESTClient,原本使用RestHighLevelClient客户端发送请求,已经移除。现使用新客户端ElasticsearchClient,网上很多高级组合检索还是老版本的,查询比较费劲,现整理一份以便使用。简单的索引、文档以及操作请参考如下:elasticsearch整合java使用创建索引、指
- Python3 搭建本地 PyPi 源
极客点儿
#Pythonpythonpip
搭建本地PyPi源的方式有很多,也有很多软件,较常用就是在官方PyPi中自带的pypiserver包。1.安装pypiserverpipinstallpypiserver2.启动pypiserverpypi-server3.上传Python包将我们打包好的Python包放到~/packages目录下,tar和whl都可以。4.远程上传Python包创建~/.pypirc文件,添加如下内容:[dis
- 同步清华镜像源,制作本地pip镜像源
淡若静水Summer
pippippip源
同步清华镜像源,制作本地pip镜像源访问清华源下载建立索引启动pip服务客户端测试为了方便国内用户使用pip模块,国内很多已经配置专用的pip镜像源国内镜像源阿里云http://mirrors.aliyun.com/pypi/simple/豆瓣http://pypi.douban.com/simple/清华大学https://pypi.tuna.tsinghua.edu.cn/simple/中国科
- 搭建python本地源
weixin_34234829
python开发工具
1.安装pip工具[root@tongc-yum162~]#wgethttps://files.pythonhosted.org/packages/d3/3e/1d74cdcb393b68ab9ee18d78c11ae6df8447099f55fe86ee842f9c5b166c/setuptools-40.0.0.zip[root@tongc-yum162~]#cdsetuptools-40.0
- 搭建本地pip源
weixin_30721077
python运维开发工具
搭建本地的pip源开发环境部署机器的时候,每次从网上下载pip包会很慢,将需要的包和相关依赖下载到本地,搭建一个本地源服务器。基本都是安装多个包,推荐使用文件的方式,文件内容格式,可以指定版本package==1.0.0,也可以不指定package,每个包名在一行:package==1.0.0package==1.0.0package==1.0.0安装pip2pi工具安装pipinstallpip
- 解决python -m pip install --upgrade pip更新失败
svygh123
pythonpip开发语言
C:\Users\Administrator>python-mpipinstall--upgradepipLookinginindexes:https://pypi.tuna.tsinghua.edu.cn/simpleCollectingpipERROR:HTTPerror403whilegettinghttps://pypi.tuna.tsinghua.edu.cn/packages/8a/6
- Linux二进制部署K8s集群的平滑升级教程
努力的小T
KubernetesLinux云计算运维基础linuxkubernetes运维云计算容器云原生服务器
一、升级前的准备工作备份集群配置和数据备份/etc/kubernetes/目录,其中包含Kubernetes集群的配置文件。备份/var/lib/etcd/目录,其中存储了etcd数据库的数据。使用etcdctl工具备份etcd数据:bash复制ETCDCTL_API=3etcdctlsnapshotsave/data/etcd/etcd_bak.db\--endpoints=https://12
- 搭建自定义的Python pip源教程
代码编织匠人
pythonpip开发语言Python
在Python开发过程中,我们经常使用pip来安装各种Python包和库。pip是Python的包管理工具,它可以从互联网上下载并安装Python包。默认情况下,pip使用官方的Python包源,但有时我们需要搭建自己的pip源,以便在内部网络或特定环境中使用。本教程将向您展示如何在Python环境下搭建属于自己的pip源。我们将使用pip的配置文件来指定自定义源的URL,并演示如何测试和使用自定
- windows基于face_recognition实现人脸识别
Python小萝卜
计算机视觉python人脸识别pythonface_recogni
环境搭建pipinstallopencv-python--user-ihttps://pypi.tuna.tsinghua.edu.cn/simplepipinstallopencv-contrib-python--user-ihttps://pypi.tuna.tsinghua.edu.cn/simplepipinstallcmake--user-ihttps://pypi.tuna.tsing
- iOS http封装
374016526
ios服务器交互http网络请求
程序开发避免不了与服务器的交互,这里打包了一个自己写的http交互库。希望可以帮到大家。
内置一个basehttp,当我们创建自己的service可以继承实现。
KuroAppBaseHttp *baseHttp = [[KuroAppBaseHttp alloc] init];
[baseHttp setDelegate:self];
[baseHttp
- lolcat :一个在 Linux 终端中输出彩虹特效的命令行工具
brotherlamp
linuxlinux教程linux视频linux自学linux资料
那些相信 Linux 命令行是单调无聊且没有任何乐趣的人们,你们错了,这里有一些有关 Linux 的文章,它们展示着 Linux 是如何的有趣和“淘气” 。
在本文中,我将讨论一个名为“lolcat”的小工具 – 它可以在终端中生成彩虹般的颜色。
何为 lolcat ?
Lolcat 是一个针对 Linux,BSD 和 OSX 平台的工具,它类似于 cat 命令,并为 cat
- MongoDB索引管理(1)——[九]
eksliang
mongodbMongoDB管理索引
转载请出自出处:http://eksliang.iteye.com/blog/2178427 一、概述
数据库的索引与书籍的索引类似,有了索引就不需要翻转整本书。数据库的索引跟这个原理一样,首先在索引中找,在索引中找到条目以后,就可以直接跳转到目标文档的位置,从而使查询速度提高几个数据量级。
不使用索引的查询称
- Informatica参数及变量
18289753290
Informatica参数变量
下面是本人通俗的理解,如有不对之处,希望指正 info参数的设置:在info中用到的参数都在server的专门的配置文件中(最好以parma)结尾 下面的GLOBAl就是全局的,$开头的是系统级变量,$$开头的变量是自定义变量。如果是在session中或者mapping中用到的变量就是局部变量,那就把global换成对应的session或者mapping名字。
[GLOBAL] $Par
- python 解析unicode字符串为utf8编码字符串
酷的飞上天空
unicode
php返回的json字符串如果包含中文,则会被转换成\uxx格式的unicode编码字符串返回。
在浏览器中能正常识别这种编码,但是后台程序却不能识别,直接输出显示的是\uxx的字符,并未进行转码。
转换方式如下
>>> import json
>>> q = '{"text":"\u4
- Hibernate的总结
永夜-极光
Hibernate
1.hibernate的作用,简化对数据库的编码,使开发人员不必再与复杂的sql语句打交道
做项目大部分都需要用JAVA来链接数据库,比如你要做一个会员注册的 页面,那么 获取到用户填写的 基本信后,你要把这些基本信息存入数据库对应的表中,不用hibernate还有mybatis之类的框架,都不用的话就得用JDBC,也就是JAVA自己的,用这个东西你要写很多的代码,比如保存注册信
- SyntaxError: Non-UTF-8 code starting with '\xc4'
随便小屋
python
刚开始看一下Python语言,传说听强大的,但我感觉还是没Java强吧!
写Hello World的时候就遇到一个问题,在Eclipse中写的,代码如下
'''
Created on 2014年10月27日
@author: Logic
'''
print("Hello World!");
运行结果
SyntaxError: Non-UTF-8
- 学会敬酒礼仪 不做酒席菜鸟
aijuans
菜鸟
俗话说,酒是越喝越厚,但在酒桌上也有很多学问讲究,以下总结了一些酒桌上的你不得不注意的小细节。
细节一:领导相互喝完才轮到自己敬酒。敬酒一定要站起来,双手举杯。
细节二:可以多人敬一人,决不可一人敬多人,除非你是领导。
细节三:自己敬别人,如果不碰杯,自己喝多少可视乎情况而定,比如对方酒量,对方喝酒态度,切不可比对方喝得少,要知道是自己敬人。
细节四:自己敬别人,如果碰杯,一
- 《创新者的基因》读书笔记
aoyouzi
读书笔记《创新者的基因》
创新者的基因
创新者的“基因”,即最具创意的企业家具备的五种“发现技能”:联想,观察,实验,发问,建立人脉。
第一部分破坏性创新,从你开始
第一章破坏性创新者的基因
如何获得启示:
发现以下的因素起到了催化剂的作用:(1) -个挑战现状的问题;(2)对某项技术、某个公司或顾客的观察;(3) -次尝试新鲜事物的经验或实验;(4)与某人进行了一次交谈,为他点醒
- 表单验证技术
百合不是茶
JavaScriptDOM对象String对象事件
js最主要的功能就是验证表单,下面是我对表单验证的一些理解,贴出来与大家交流交流 ,数显我们要知道表单验证需要的技术点, String对象,事件,函数
一:String对象;通常是对字符串的操作;
1,String的属性;
字符串.length;表示该字符串的长度;
var str= "java"
- web.xml配置详解之context-param
bijian1013
javaservletweb.xmlcontext-param
一.格式定义:
<context-param>
<param-name>contextConfigLocation</param-name>
<param-value>contextConfigLocationValue></param-value>
</context-param>
作用:该元
- Web系统常见编码漏洞(开发工程师知晓)
Bill_chen
sqlPHPWebfckeditor脚本
1.头号大敌:SQL Injection
原因:程序中对用户输入检查不严格,用户可以提交一段数据库查询代码,根据程序返回的结果,
获得某些他想得知的数据,这就是所谓的SQL Injection,即SQL注入。
本质:
对于输入检查不充分,导致SQL语句将用户提交的非法数据当作语句的一部分来执行。
示例:
String query = "SELECT id FROM users
- 【MongoDB学习笔记六】MongoDB修改器
bit1129
mongodb
本文首先介绍下MongoDB的基本的增删改查操作,然后,详细介绍MongoDB提供的修改器,以完成各种各样的文档更新操作 MongoDB的主要操作
show dbs 显示当前用户能看到哪些数据库
use foobar 将数据库切换到foobar
show collections 显示当前数据库有哪些集合
db.people.update,update不带参数,可
- 提高职业素养,做好人生规划
白糖_
人生
培训讲师是成都著名的企业培训讲师,他在讲课中提出的一些观点很新颖,在此我收录了一些分享一下。注:讲师的观点不代表本人的观点,这些东西大家自己揣摩。
1、什么是职业规划:职业规划并不完全代表你到什么阶段要当什么官要拿多少钱,这些都只是梦想。职业规划是清楚的认识自己现在缺什么,这个阶段该学习什么,下个阶段缺什么,又应该怎么去规划学习,这样才算是规划。
- 国外的网站你都到哪边看?
bozch
技术网站国外
学习软件开发技术,如果没有什么英文基础,最好还是看国内的一些技术网站,例如:开源OSchina,csdn,iteye,51cto等等。
个人感觉如果英语基础能力不错的话,可以浏览国外的网站来进行软件技术基础的学习,例如java开发中常用的到的网站有apache.org 里面有apache的很多Projects,springframework.org是spring相关的项目网站,还有几个感觉不错的
- 编程之美-光影切割问题
bylijinnan
编程之美
package a;
public class DisorderCount {
/**《编程之美》“光影切割问题”
* 主要是两个问题:
* 1.数学公式(设定没有三条以上的直线交于同一点):
* 两条直线最多一个交点,将平面分成了4个区域;
* 三条直线最多三个交点,将平面分成了7个区域;
* 可以推出:N条直线 M个交点,区域数为N+M+1。
- 关于Web跨站执行脚本概念
chenbowen00
Web安全跨站执行脚本
跨站脚本攻击(XSS)是web应用程序中最危险和最常见的安全漏洞之一。安全研究人员发现这个漏洞在最受欢迎的网站,包括谷歌、Facebook、亚马逊、PayPal,和许多其他网站。如果你看看bug赏金计划,大多数报告的问题属于 XSS。为了防止跨站脚本攻击,浏览器也有自己的过滤器,但安全研究人员总是想方设法绕过这些过滤器。这个漏洞是通常用于执行cookie窃取、恶意软件传播,会话劫持,恶意重定向。在
- [开源项目与投资]投资开源项目之前需要统计该项目已有的用户数
comsci
开源项目
现在国内和国外,特别是美国那边,突然出现很多开源项目,但是这些项目的用户有多少,有多少忠诚的粉丝,对于投资者来讲,完全是一个未知数,那么要投资开源项目,我们投资者必须准确无误的知道该项目的全部情况,包括项目发起人的情况,项目的维持时间..项目的技术水平,项目的参与者的势力,项目投入产出的效益.....
- oracle alert log file(告警日志文件)
daizj
oracle告警日志文件alert log file
The alert log is a chronological log of messages and errors, and includes the following items:
All internal errors (ORA-00600), block corruption errors (ORA-01578), and deadlock errors (ORA-00060)
- 关于 CAS SSO 文章声明
denger
SSO
由于几年前写了几篇 CAS 系列的文章,之后陆续有人参照文章去实现,可都遇到了各种问题,同时经常或多或少的收到不少人的求助。现在这时特此说明几点:
1. 那些文章发表于好几年前了,CAS 已经更新几个很多版本了,由于近年已经没有做该领域方面的事情,所有文章也没有持续更新。
2. 文章只是提供思路,尽管 CAS 版本已经发生变化,但原理和流程仍然一致。最重要的是明白原理,然后
- 初二上学期难记单词
dcj3sjt126com
englishword
lesson 课
traffic 交通
matter 要紧;事物
happy 快乐的,幸福的
second 第二的
idea 主意;想法;意见
mean 意味着
important 重要的,重大的
never 从来,决不
afraid 害怕 的
fifth 第五的
hometown 故乡,家乡
discuss 讨论;议论
east 东方的
agree 同意;赞成
bo
- uicollectionview 纯代码布局, 添加头部视图
dcj3sjt126com
Collection
#import <UIKit/UIKit.h>
@interface myHeadView : UICollectionReusableView
{
UILabel *TitleLable;
}
-(void)setTextTitle;
@end
#import "myHeadView.h"
@implementation m
- N 位随机数字串的 JAVA 生成实现
FX夜归人
javaMath随机数Random
/**
* 功能描述 随机数工具类<br />
* @author FengXueYeGuiRen
* 创建时间 2014-7-25<br />
*/
public class RandomUtil {
// 随机数生成器
private static java.util.Random random = new java.util.R
- Ehcache(09)——缓存Web页面
234390216
ehcache页面缓存
页面缓存
目录
1 SimplePageCachingFilter
1.1 calculateKey
1.2 可配置的初始化参数
1.2.1 cach
- spring中少用的注解@primary解析
jackyrong
primary
这次看下spring中少见的注解@primary注解,例子
@Component
public class MetalSinger implements Singer{
@Override
public String sing(String lyrics) {
return "I am singing with DIO voice
- Java几款性能分析工具的对比
lbwahoo
java
Java几款性能分析工具的对比
摘自:http://my.oschina.net/liux/blog/51800
在给客户的应用程序维护的过程中,我注意到在高负载下的一些性能问题。理论上,增加对应用程序的负载会使性能等比率的下降。然而,我认为性能下降的比率远远高于负载的增加。我也发现,性能可以通过改变应用程序的逻辑来提升,甚至达到极限。为了更详细的了解这一点,我们需要做一些性能
- JVM参数配置大全
nickys
jvm应用服务器
JVM参数配置大全
/usr/local/jdk/bin/java -Dresin.home=/usr/local/resin -server -Xms1800M -Xmx1800M -Xmn300M -Xss512K -XX:PermSize=300M -XX:MaxPermSize=300M -XX:SurvivorRatio=8 -XX:MaxTenuringThreshold=5 -
- 搭建 CentOS 6 服务器(14) - squid、Varnish
rensanning
varnish
(一)squid
安装
# yum install httpd-tools -y
# htpasswd -c -b /etc/squid/passwords squiduser 123456
# yum install squid -y
设置
# cp /etc/squid/squid.conf /etc/squid/squid.conf.bak
# vi /etc/
- Spring缓存注解@Cache使用
tom_seed
spring
参考资料
http://www.ibm.com/developerworks/cn/opensource/os-cn-spring-cache/
http://swiftlet.net/archives/774
缓存注解有以下三个:
@Cacheable @CacheEvict @CachePut
- dom4j解析XML时出现"java.lang.noclassdeffounderror: org/jaxen/jaxenexception"错误
xp9802
java.lang.NoClassDefFoundError: org/jaxen/JaxenExc
关键字: java.lang.noclassdeffounderror: org/jaxen/jaxenexception
使用dom4j解析XML时,要快速获取某个节点的数据,使用XPath是个不错的方法,dom4j的快速手册里也建议使用这种方式
执行时却抛出以下异常:
Exceptio
 to be
to be .
.  .
.  ,
,  /4 to obtain the series
/4 to obtain the series , one would need to use at least 10^50 terms of this expansion!
, one would need to use at least 10^50 terms of this expansion! ,
,  /6 to obtain the series
/6 to obtain the series .
. ,
, 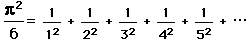

 in terms of the Fibonacci numbers,
in terms of the Fibonacci numbers,  .
.