Binary Indexed Tree （树状数组）

树状数组是能够完成下述操作的数据结构

给一个初始值全为0的数列a1,a2,…an。

*给定i，计算a1+a2+…+ai

*给定i和x，执行ai += x

1.基于线段树的实现

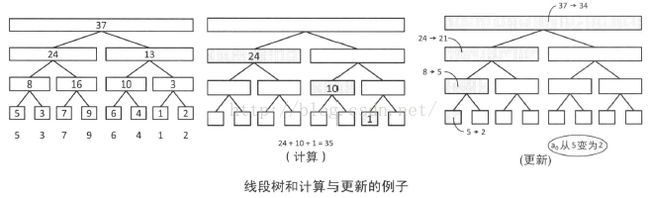
如果使用线段树，只需要对RMQ的样例做少许修改就可以实现这两个功能。线段树的每个节点上维护的是对应的区间的和。

接下来，我们来看如何计算从s到t的和。在基于线段树的实现中，这个和是可以直接求得的。

但是如果我们能够计算（从1到t的和）—（从1到s-1的和），同样可以得到s到t的和。也就是说，只要对于任意i，我们都能计算出1到i的部分和就足够了。

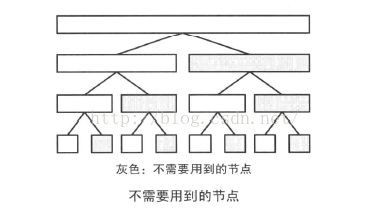
在这样的限制下，会带来哪些改变呢？我们可以发现，线段树上每个节点的右儿子的值都不需要了（在计算时如果要使用这个点的值，那么它的左边的兄弟的值也一定会用到，这个时候只需要使用它们的父亲的值就可以了）。

基于上面的思路得到的数据结构就是BIT。比起线段树，BIT实现起来更方便，速度也更快。

2.BIT的结构

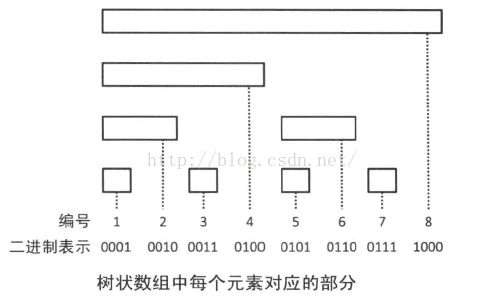
BIT使用数组维护下图所示的部分和

也就是把线段树中不需要的节点去掉之后，再把剩下的节点对应到数组中。让我们对比每个节点对应的区间的长度和节点编号的二进制表示。以1结尾的1,3,5,7的长度是1，最后有1个0的2,6的长度是2，最后有2个0的4的长度是4….这样，编号的二进制表示就能够和区间非常容易地对应起来。利用这个性质，BIT可以通过非常简单的位运算实现。

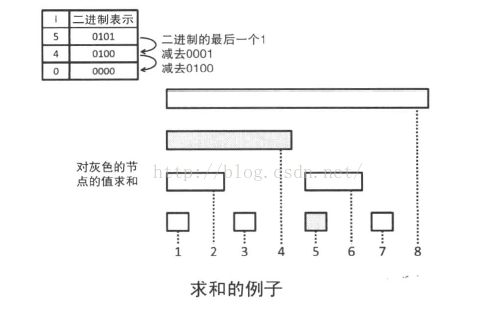
3.BIT的求和

计算前i项的和需要从i开始，不断把当前位置i的值加到结果中，并从i中减去i的二进制最低位非0位对应的幂，直到i变成0为止。i的二进制的最后一个1可以通过i&-i得到。

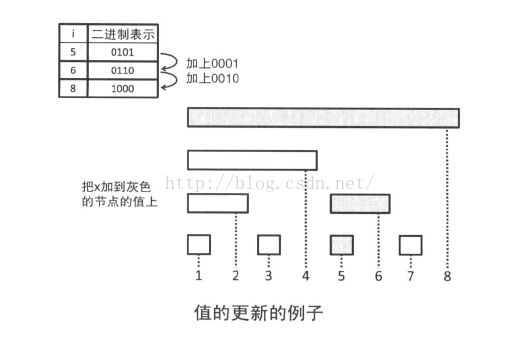
4.BIT的值的更新

使第i项的值增加x需要从i开始，不断把当前位置i的值增加x，并把i的二进制最低非0位对应的幂加到i上。

5.BIT的复杂度

总共需要对O(logn)个值进行操作，所有复杂度是O(logn)。

6.BIT的实现

顺便提一下，i-=i&-i也可以写作i=i&(i-1)。

 

//[1, n]
int bit[maxn + 1], n;

int sum(int i)
{
    int s = 0;
    while (i > 0){
        s += bit[i];
        i -= i & -i;
    }
    return s;
}

void add(int i, int x)
{
    while (i <= n){
        bit[i] += x;
        i += i & -i;
    }
}

7.二维BIT

BIT可以方便的扩展到二维的情况。对于W*H的二维BIT只需要建立H个大小为x轴方向元素个数W的BIT，然后把这些BIT通过y轴方向的BIT管理起来就可以了。也就是说，y轴方向的BIT的每个元素不是整数，而是一个x轴方向的BIT。这样所有操作的复杂度都是O(logW * logH)。用同样的方法可以扩展到更高维度的情况。