递归与迭代_1 2016.4.21

迭代乃人工，递归方神通

To interate is human，to recurse，divine

一、定义

（1）
迭代
是重复反馈过程的活动，其目的通常是为了逼近所需目标或结果
每一次对过程的重复称为一次“迭代”，而每一次迭代得到的结果会作为下一次迭代的初始值

（2）
①
程序调用自身的编程技巧称为递归（ recursion）

一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法，它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解，递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算，大大地减少了程序的代码量

递归的能力在于用有限的语句来定义对象的无限集合

一般来说，递归需要有边界条件、递归前进段和递归返回段
当边界条件不满足时，递归前进
当边界条件满足时，递归返回

②
递归，就是在运行的过程中调用自己
构成递归需具备的条件：
1. 子问题须与原始问题为同样的事，且更为简单
2. 不能无限制地调用本身，须有个递归出口，化简为非递归状况处理

③
斐波纳契数列是典型的递归案例：

Fib(0) = 1 [基本情况]
Fib(1) = 1 [基本情况]
对所有n > 1的整数：Fib(n) = (Fib(n-1) + Fib(n-2)) [递归定义]

尽管有许多数学函数均可以递归表示，但在实际应用中，递归定义的高开销往往会让人望而却步

阶乘（1) = 1 [基本情况]
对所有n > 1的整数：阶乘（n) = (n * 阶乘（n-1)) [递归定义]

④
一种便于理解的心理模型
是认为递归定义对对象的定义是按照“先前定义的”同类对象来定义的

例如：你怎样才能移动100个箱子？
答案：你首先移动一个箱子，并记下它移动到的位置
然后再去解决较小的问题：你怎样才能移动99个箱子？
最终，你的问题将变为怎样移动一个箱子，而这时你已经知道该怎么做的

二、C语言对递归的支持

由于使用的调用栈，C语言自然支持了递归

在C语言的函数中，调用自己和调用其他函数并没有任何本质区别，都是建立新栈帧，传递参数并修改“当前代码行”

在函数执行完毕后删除栈帧，处理返回值并修改“当前代码行”

可以作如下的比喻：

皇帝（拥有 mian 函数的栈帧）：大臣，你给我算一下 f(3)
大臣（拥有 f(3) 的栈帧）：知府，你给我算一下 f(2)
知府（拥有 f(2) 的栈帧）：县令，你给我算一下 f(1)
县令（拥有 f(1) 的栈帧）：师爷，你给我算一下 f(0)
师爷（拥有 f(0) 的栈帧）：回老爷， f(0) = 1
县令：（心算 f(1) = f(0)*1 = 1 ） 回知府大人，f(1) = 1
知府：（心算 f(2) = f(1)*2 = 2 ） 回大人，f(2) = 2
大臣：（心算 f(3) = f(2)*3 = 6 ） 回皇上，f(3) = 6
皇帝满意了

不理解调用栈，不必强求–知道递归为什么能正常工作就行

设计递归程序的重点在于给下级安排工作

每次递归调用都需要往调用栈里增加一个栈帧，久而久之就越界了。
用术语就把它叫做栈溢出（Stack Overflow）

局部变量也是放在堆栈段的，所以建议”把较大的数组放在 main 函数外“

栈溢出不见得是递归调用太多，也可能是局部变量太大

只要总大小超过了允许的范围，就会产生栈溢出

三、特点、区别

递归算法是一种直接或者间接地调用自身算法的过程
在计算机编写程序中，递归算法对解决一大类问题是十分有效的，它往往使算法的描述简洁而且易于理解

递归算法解决问题的特点：
(1)
递归就是在过程或函数里调用自身
(2)
在使用递归策略时，必须有一个明确的递归结束条件，称为递归出口
(3)
递归算法解题通常显得很简洁，但递归算法解题的运行效率较低
所以一般不提倡用递归算法设计程序。
(4)
在递归调用的过程当中系统为每一层的返回点、局部量等开辟了栈来存储
递归次数过多容易造成栈溢出等

四、递归应用

(1)数据的定义是按递归定义的（Fibonacci函数）
(2)问题解法按递归算法实现
这类问题虽则本身没有明显的递归结构，但用递归求解比迭代求解更简单，如Hanoi（汉诺塔）问题
(3)数据的结构形式是按递归定义的
如二叉树、广义表等，由于结构本身固有的递归特性，则它们的操作可递归地描述

递归的缺点：
递归算法解题相对常用的算法如普通循环等，运行效率较低
因此，应该尽量避免使用递归，除非没有更好的算法或者某种特定情况，递归更为适合的时候
在递归调用的过程当中系统为每一层的返回点、局部量等开辟了栈来存储
递归次数过多容易造成栈溢出等

五、线性递归

（1）
数组求和：迭代
问题：计算给定的n个整数之和
实现：逐一取出个元素，累加之

int Sum(int num[], int n)
{
    int sum = 0;
    for (int i=0; i<n; ++i) {
        sum += num[i];
    }
    return sum;
}

数组求和：递归

若n = 0则总和必为0，这也是最终的平凡情况
否则一般地，总和可理解为前n-1个整数 （num[0, n - 1]）之和，再加上末尾元素（num[n - 1]）

按这一思路，可基于线性递归模式，设计出算法

int Sum(int num[], int n)   //数组求和算法（线性递归版）
{
    if (n < 1) {    //平凡情况，递归基
        return 0;   //直接（非递归式）计算
    } else {        //一般情况
        return Sum(num, n-1) + num[n-1];   //递归：前n-1项之和，再累计第n-1项
    }
}
//O(1)*递归深度 = O(1) * (n+1) = O(n)

由此实例，可以看出保证递归算法有穷性的基本技巧：
首先判断并处理n = 0之类的平凡情况，以免因无限递归而导致系统溢出
这类平凡情况统称“递归基”（base case of recursion）
平凡情况可能有多种，但至少要有一种（比如此处），且迟早必然会出现

（2）
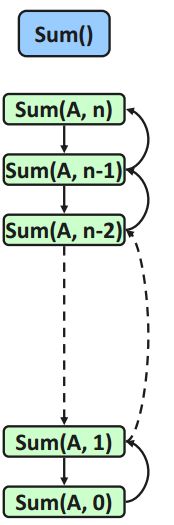
线性递归
算法Sum()可能朝着更深一层进行自我调用，且每一递归实例对自身的调用至多一次
于是，每一层次上至多只有一个实例，且他们构成一个线性的次序关系
此类递归模式因而称作“线性递归”（linear recursion）
它也是递归的最基本的形式

这种形式中，应用问题总可分解为两个独立的子问题：
其一对应于单独的某个元素，故可直接求解（比如 num[n - 1]）
另一个对应于剩余部分，且其结构与原问题相同（比如 num[0, n-1]）
另外，子问题的解经简单的合并（比如整数相加）之后，即可得到原问题的解

减而治之
线性递归的模式，往往对应于所谓减而治之（decrease - and - conquer）的算法策略：
递归每深入一层，待求问题的规模都缩减一个常数，直至最终蜕化为平凡的小（简单）问题

按照减而治之的策略，此处随着递归的深入，调用参数将单调地线性递减
因此无论最初输入的n有多大，递归调用的总次数都是有限的，估算法的执行迟早会终止，既满足有穷性
当抵达递归基时，算法将执行非递归的计算（这里是返回0）

六、递归分析

递归算法时间和空间复杂度的分析与常规算法很不一样，有其自身的规律和特定的技巧
以下介绍递归跟踪与递推方程这两种主要的方法

（1）递归跟踪
作为一种直观且可视的方法，递归跟踪（recursion trace）可用以分析递归算法的总体运行时间与空间
直观形象 ，仅适用于简明的递归模式

递归跟踪（recursion trace）分析
检查每个递归实例
除调用语句本身，统计其它代码所需时间
其总和即算法执行时间

C语法的灵活性，会给分析带来一定困难 //多读代码 + 遵从规范

整个算法所需的计算时间，应该等于所有递归实例的创建、执行和销毁所需的时间总和
其中，递归实例的创建、销毁均由操作系统负责完成，其对应的时间成本通常可以近似为常数，不会超过递归实例中实质计算步骤所需的时间成本，故往往均予忽略
为便于估算，启动各实例的每一条递归调用语句所需的时间，也可以计入被创建的递归实例的账上
如此我们只需统计各递归实例中非递归调用部分所需的时间

具体的，就以上的Sum()算法而言，每一递归实例中非递归部分涉及的计算无非三类（判断n是否为0、累加Sum(n - 1)与num[n - 1]、返回当前总和），且至多各执行一次
鉴于它们均属于基本操作，每个递归实例实际所需的时间都应为O(3)

对于长度为n的输入数组，递归深度应为n+1
故整个Sum算法的运行时间为：
(n + 1) * O(3) = O(3 * (n + 1)) = O(n)

算法的空间复杂度：
在创建了最后一个递归实例（即到达递归基）时，占用的空间量达到最大–准确地说，等于所有递归实例各自所占空间量的总和
这里每一递归实例所需存放的数据，无非是调用参数（数据的起始地址和长度）以及用于累加总和的临时变量
这些数据各自只需常数规模的空间，其总量也应为常数
故此可知，Sum()算法的空间复杂度线性正比于其递归的慎独，亦即O(n)

（2）递推方程（间接抽象，更适用于复杂的递归模式）
递归算法的另一常用的分析方法，即递推方程（recurrence equation）法
与递归跟踪分析相反，该方法无需绘出具体的调用过程，而是对递归模式的数学归纳，导出复杂度定界函数的递推方程（组）及其边界条件，从而将复杂度的分析，转化为递归方程（组）的求解

在总体思路上，该方法与微分方程法颇为相似：
很多复杂函数的显示表达通常不易直接获得，但是它们的微分形式却往往遵循某些相对简洁的规律，通过求解描述这些规律的一组微分方程，即可最终导出原函数的显式表示
微分方程的解通常并不唯一，除非给定足够多的边界条件

类似的，为使复杂度定界函数的递推方程能够给出确定的解，也需要给定某些边界条件

边界条件往往可以通过对递归基的分析而获得

（3）
找最大元素：迭代
问题：在给定的n个整数中，找出最大者
算法Max(num[ ], n)：逐一检查各元素，保留最大者
O(n)

int Max(int num[], int n)
{
    int Max = num[0];
    for (int i=1; i<n; ++i) {
        if (num[i] > Max) {
            Max = num[i];
        }
    }
    return Max;
}

找最大元素：递归

int Max(int num[], int low, int high)
{
    if (low == high) {
        return num[low];
    } else {
        int mid = (low+high) / 2;
        return max(Max(num, low, mid), Max(num, mid+1, high));
    }
}

从递推的角度看，为求解Max(num, lo, hi)
需递归求解Max(num, lo, mi)和Max(num, mi+1, hi)
进而在子问题的解中取大者
递归基：Max(num, lo, lo)

七、递归模式

（1）多递归基
为保证有穷性，递归算法都必须设置递归基，且确保总能执行到
为此，针对每一类可能出现的平凡情况，都需设置对应的递归基
故同一算法的递归基可能（显式或隐式地）不止一个

数组倒置问题，也就是将数组中各元素的次序前后反转。
比如，若输入数组为：A[] = {3, 1, 4, 1, 5, 9, 2, 6}
则倒置后为：A[] = {6, 2, 9, 5, 1, 4, 1, 3}

void Reverse(int* num, int low, int high)   //数组倒置（多递归基迭代版）
{
    if (low < high) {
        swap(num[low], num[high]);  //交换num[low]和num[high]
        Reverse(num, low+1, high-1);    //递归倒置num(low, high)
    }   // else 隐含了两种递归基
}   //O(high - low + 1) 

void Reverse(int* num, int low, int high)   //数组倒置 迭代版
{
    while (low < high) {
        swap(num[low], num[high]);
        ++low;
        --high;
    }
}

（2）实现递归
在设计递归算法时，往往需要从多个角度反复尝试，方能确定对问题的输入及其规模的最佳划分方式
有时，还可能需要从不同的角度重新定义和描述原问题，使得经分解所得的子问题与原问题具有相同的语义形式

例如，线性迭代版Reverse()算法中，通过引入参数low和high，使得对全数组以及其后各子数组的递归调用都统一为相同的语法形式

（3）多向递归
递归算法中，不仅递归基可能有多个，递归调用也可能有多种可供选择的分支

以下的简单实例中，每一递归实例虽有多个可能的递归方向，但只能从中选择其一，故各层次上的递归实例依然构成一个线性次序关系，这种情况依然属于线性递归

typedef long long LL;

LL power2(int n)    //幂函数2^n算法（暴力迭代版），n>=0
{
    LL pow = 1;
    while (n > 0) {
        --n;
        pow <<= 1;
    }
    return pow;
}   //O(n) = O(2^r) r为输入指数n的比特位数

LL power2(int n)    //幂函数2^n算法（线性递归版），n>=0
{
    if (n == 0) {
        return 1;
    } else {
        return power2(n-1)*2;
    }
}   //O(n)

实际上，若能从其它角度分析函数并给出新的递归定义，完全可以更为快速地完成幂函数的计算

以下就是一例：
power2(n)
若n = 0，power2(n) = 1
若n >0 and odd，power2(n) = power2(⌊n/2⌋)^2 * 2
若n > 0 and even，power2(⌊n/2⌋)^2

按照这一新的表述和理解，可按二进制展开n之后的各比特位，通过反复的平方运算和加倍运算得到power2(n)

比如：

2^1 = 2^001(b) = (2^2^2)^0 * (2^2)^0 * 2^1 = (((1 * 2^0)^2 * 2^0)^2 * 2^1)

2^2 = 2^010(b) = (2^2^2)^0 * (2^2)^1 * 2^0= (((1 * 2^0)^2 * 2^1)^2 * 2^0)

2^3 = 2^011(b) = (2^2^2)^0 * (2^2)^1 * 2^1 = (((1 * 2^0)^2 * 2^1)^2 * 2^1)

2^4 = 2^100(b) = (2^2^2)^1 * (2^2)^0 * 2^0 = (((1 * 2^1)^2 * 2^0)^2 * 2^0)

2^5 = 2^101(b) = (2^2^2)^1 * (2^2)^0 * 2^1 = (((1 * 2^1)^2 * 2^0)^2 * 2^1)

2^6 = 2^110(b) = (2^2^2)^1 * (2^2)^1 * 2^0 = (((1 * 2^1)^2 * 2^1)^2 * 2^0)

2^7 = 2^111(b) = (2^2^2)^1 * (2^2)^1 * 2^1 = (((1 * 2^1)^2 * 2^1)^2 * 2^1)
。。。

一般地，若n的二进制展开式为b1b2b3…bk，则有
2^n = (…(((1 * 2^b1)^2 * 2^b2)^2) * 2^b3)^2 … * 2^bk)

若nk-1和nk的二进制展开式分别为b1b2…bk-1和b1b2…bk-1bk，则有
2^nk = (2^nk-1)^2 * 2bk

由此归纳得出如下递推式：
power2(nk)
若bk = 1，power2(nk) = power2(nk-1)^2 * 2
若bk = 0，power2(nk) = power2(nk-1)^2

inline LL squre(LL a)
{
    return a*a;
}

LL power2(int n)    //幂函数2^n算法（优化递归版），n>=0
{
    if (n == 0) {
        return 1;   //递归基；否则，视n的奇偶分别递归
    } else {
        return (n&1) ? squre(power2(n>>1)) << 1 : squre(power2(n>>1));
    }
}   //O(logn) = O(r)，r为输入指数n的比特位数

针对输入参数n为奇数或偶数的两种可能，这里分别设有不同的递归方向
尽管如此，每个递归实例都只能沿其中的一个方向深入到下层递归
故仍然属于线性递归

该算法的时间复杂度为：
o(logn) * O(1) = O(logn) = O(r)

与此前暴力版本的O(n) = O(2^r)相比，计算效率得到了极大的提高

LL power(int x, int n)    //幂函数x^n算法（迭代优化版），n>=0
{
    LL pow = 1;
    LL t = x;
    while (n) {
        if (n&1) {
            pow *= t;
        }
        t *= t;
        n >>= 1;
    }
    return pow;
}   //O(logn) = O(r)，r为输入指数n的比特位数

选自：
《数据结构（C++语言版）（第三版）》邓俊辉
《算法竞赛入门经典》刘汝佳
百度百科
博客（忘了及时存网址，实在不好意思）
略有改动