安卓自定义View之贝塞尔曲线简单使用

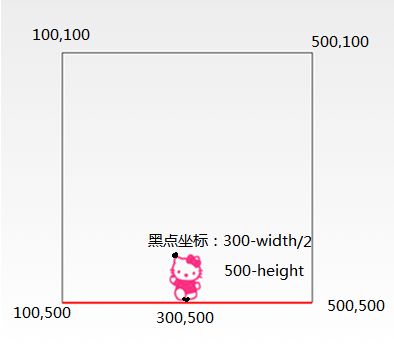
一个正方形框框，底边是一条贝塞尔曲线，上面站着个helloKitty，向下拉动曲线，HelloKitty上弹，但是不会超过正方形上边框。

bitmap的绘制坐标从左上角算起。

我这儿没用到物理引擎，速度方向等等那么复杂的，就简单的实现。

首先，构造方法中初始化一些东西

public ViewTwo(Context context, AttributeSet attrs,int defStyle) {
        super(context, attrs,defStyle);
        // TODO Auto-generated constructor stub
        paint=new Paint();
        paint.setColor(Color.BLACK);
        paint.setStrokeWidth(7f);
        paint.setAntiAlias(true);
        path=new Path();
        //这种写法，有效避免内存溢出
        options=new Options();
        options.inJustDecodeBounds=true;
        //qqq为资源图片
        bitmap=BitmapFactory.decodeResource(getResources(), R.drawable.qqq,options);
        //inSampleSize属性是为了节省内存
        options.inSampleSize=options.outHeight/90;
        //下面计算得到缩略图（可等比例放大缩小）的宽和高，本来图片是60*60，我把它放到90*90，outwidth为bitmap的宽度
        options.outWidth=options.outWidth*90/options.outHeight;
        options.outHeight=90;
        options.inJustDecodeBounds=false;
        bitmap=BitmapFactory.decodeResource(getResources(), R.drawable.qqq,options);
    }

接下来，onDraw中先画正方形

/***画正方形*/
        paint.reset();
        //4条线，每条线一个初始点和结束点坐标
        float[] pts={100,500,500,500,
                     100,100,500,100,
                     100,100,100,500,
                     500,100,500,500};
                     //第二个第三个参数为跳过前4个数据，只画出后面12个
        canvas.drawLines(pts,4,12, paint);

再画贝塞尔曲线，x,y为辅助点坐标，下面会提供

/***画贝塞尔*/
        paint.reset();
        //画笔颜色
        paint.setColor(Color.RED);
        //画出不填充的图形
        paint.setStyle(Paint.Style.STROKE);
        //参数越大线条越粗
        paint.setStrokeWidth(3f);
        //必须重置path，不然会出现many曲线，还不消失
        path.reset();
        //起点坐标
        path.moveTo(100, 500);
        //x,y为辅助点坐标，500，500为终点坐标
        path.quadTo(x, y, 500, 500);
        canvas.drawPath(path, paint);
        /***画出辅助点，可以看出轨迹*/
        canvas.drawPoint(x, y, paint);

画hellokitty

/***画小人，为了将hellokitty画到曲线中央，下面提供xp,yp的计算方法*/
         canvas.drawBitmap(bitmap, xp-options.outWidth/2, yp-options.outHeight, paint);
          invalidate();

重写onTouchEvent方法，当手指拉动的时候，得出手指的坐标点，

public boolean onTouchEvent(MotionEvent event) {
        // TODO Auto-generated method stub
        switch (event.getAction()) {
        case MotionEvent.ACTION_MOVE:
            x=event.getX();
            y=event.getY();
            /***t的范围从0-0.5就是从起始点到终点曲线上的点坐标, * xp中100是起始点横坐标，x是辅助点的横坐标，500是终点的横坐标 yp中500是起始点纵坐标，y是辅助点的纵坐标，500是终点的纵坐标 **/
            //if是禁止上拉
            if(y<500){y=500;}
            //for(float t=0;t<=0.5;t+=0.1){
            float t=(float) 0.5;
            //xp,yp是贝塞尔曲线中点坐标，调节下面y的大小可以控制在拉动的时候图片距离横线的距离
           xp = (1-t)*(1-t)* 100 + 2* t*(1-t)* x + t * t * 500;
           yp = (1-t)*(1-t)* 500 + 2* t*(1-t)* y + t * t * 500;
            //}
            //postInvalidate()方法是在子线程中刷新View
            //invalidate()方法是在UI线程中刷新View
            invalidate();
            break;
            //ACTION_UP为松开手势状态，让曲线回到直线状态
        case MotionEvent.ACTION_UP:
            //让曲线回到直线状态
            x=300;
            y=500;
            //这儿的标志是判断kitty是否jump，发生下拉动作，所以jump
            jump = true;
            invalidate();
        }
        return true;
    }

下面根据这个标志jump写相应的动作

if (jump) {  
                /***画贝塞尔，用jumppercent这个方法是参考的别人的方法，将跳动高度化为100份，逐次递减5，在递减控制在正方形上边界内*/
                if(jumpPercent >0) {  
                //只要小于100（意味着跳出了上边界，return阻止继续上升），
                    if((yp-options.outHeight)*jumpPercent/100<=100){
                        canvas.drawBitmap(bitmap, xp-options.outWidth/2, 100, paint);  
                        jumpPercent -=5;  
                        xp=300;
                        yp=500;
                        postInvalidateDelayed(20);
                        return;
                    }
                        canvas.drawBitmap(bitmap, xp-options.outWidth/2, (yp-options.outHeight)* jumpPercent/100, paint);  
                        jumpPercent -=5;  
                        xp=300;
                        yp=500;
                        postInvalidateDelayed(20);
                }else { 
                //重置 
                        jumpPercent = 100;  
                        jump = false;  
                }
            }

我知道没图片没人来 - -！

初学，有不对的地方欢迎大家指正。 下面再去学习一下用物理引擎怎么做.

附上源码地址：https://github.com/qht1003077897/-view-.git