应用Fast ICP进行点集或曲面配准 算法解析
转载博客:http://blog.csdn.net/viewcode/article/details/8426846 供自己学习
1. ICP算法的一些网络资源
2. 经典ICP算法的步骤
3. fast ICP算法
ICP(Iterative closest points)算法是点集配准的经典算法,算法基本原理是在A method for registration of 3-D shapes文章中提出。后人也在此基础上不断和补充ICP算法。
1. 下面是介绍ICP算法的一些网络资源:
ICP算法基本介绍:
http://en.wikipedia.org/wiki/Iterative_closest_point
http://plum.eecs.jacobs-university.de/download/3dim2007/node2.html
http://baike.baidu.com/view/1954001.htm
经典ICP算法论文:
http://eecs.vanderbilt.edu/courses/cs359/other_links/papers/1992_besl_mckay_ICP.pdf
ICP算法源码下载C++:icp算法源码
Fast ICP论文地址:
http://docs.happycoders.org/orgadoc/graphics/imaging/fasticp_paper.pdf
fast icp source code C++源码:FastICP源码
http://gfx.cs.princeton.edu/proj/trimesh2/, 大家不容易找到,是因为工程的名字不叫fasticp,而是trimesh2
算法的一些实现总结:
http://www.mrpt.org/Iterative_Closest_Point_(ICP)_and_other_matching_algorithms
2. 经典ICP算法介绍。
ICP算法有较多的数学公式和概念,数学公式总归看起来费劲,这里只简要的理解下其算法步骤:
两个点集P1,P2,每一步迭代,都朝着距离最小的目标进行。
a. 筛选点对:由P1中的点,在P2中搜索出其最近的点,组成一个点对;找出两个点集中所有的点对。点对集合相当于进行有效计算的两个新点集。
b. 根据点集对,即两个新点集,计算两个重心。
c. 由新点集,计算出下一步计算的旋转矩阵R,和平移矩阵t(其实来源于重心的差异)。
d. 得到旋转矩阵和平移矩阵Rt,就可以计算点集P2进行刚体变换之后的新点集P2`,由计算P2到P2`的距离平方和,以连续两次距离平方和之差绝对值,作为是否收敛的依据。若小于阈值,就收敛,停止迭代。
e. 重复a-e,直到收敛或达到既定的迭代次数。
--其中,计算旋转矩阵R时,需要矩阵方面的运算。
由新的点集,每个点到重心的距离关系,计算正定矩阵N,并计算N的最大特征值及其最大特征向量;其特征向量等价于旋转的四元数(且是残差和最小的旋转四元数),将四元数就可以转换为旋转矩阵。
数学概念:
四元数:http://baike.soso.com/v113161.htm?ch=ch.bk.innerlink
正定矩阵:特征值都大于0的矩阵。
这些是矩阵理论,最优化原理方面的一些概念。
3. fast ICP解析:
Fast ICP是对ICP的改进与扩展。论文Efficient Variants of the ICPalgorithm详细给出了影响ICP算法的各种因素,且每种因素都哪些算法,其结果与性能如何。
Fast ICP根据这些因素将ICP算法分为6个步骤:
a. 筛选:点集或曲面的筛选(滤波)
b. 匹配:两个点集之间的点进行配对
c. 权重:给每个匹配的点对分配权重
d. 去除:去除不符合条件的点对
e. 误差度量:基于以上点对,给出每个点对的误差计算方法
f. 最小化:最小化误差度量
为测试以上阶段中不同算法的性能和结果,论文提供了三个测试场景,并在这些点集(曲面)上加上噪声:
比较平滑的波纹: 比较简单的场景,几何尺度变换不是很大
较复杂的不规则的草原地形: 相对复杂的,包含不同尺度的细节
仅含有突出一个十字形雕刻面的平面: 对匹配而言,最困难的场景,因为特征太少
下面是每个阶段的算法的比较:
a. 筛选:点集或曲面的筛选(滤波)
筛选也有以下几种策略:
* 应用点集内所有可用的点: 无疑是性能最差的方法
* 采用均匀分布的方式筛选(或是距离等间隔筛选)
* 随机筛选法
* 根据点的密度,颜色来筛选
* 对一个点集进行筛选,或者两个点集都进行筛选:对于一般的点集,两种方法收敛率和结果基本相同,但仅对一个点集筛选的算法,数据运算量相对比较大。
* 另外一个筛选策略是依据向量的分布情况: 筛选哪些能使点的向量的分布尽量大的点,这样的目的是突出 特征很少的 点集的特征 (如十字雕刻面)
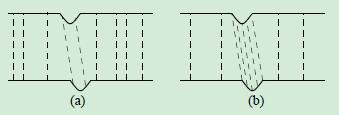
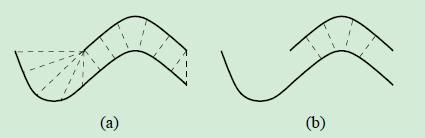
如下图 a 随机采用法, 图b是向量空间分布法 的示意图。 由图可以明显看出,空间向量分布法对点集的较少的特征有着比较好的提取能力。
Fast ICP暂不考虑一个点的密度颜色信息。 对均匀分布法、随机法、向量空间分布法比较。
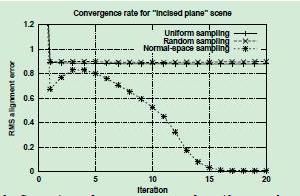
对水波等简单场景下:其收敛速度和收敛效果都差别不大。但对于特征点较少的场景,向量空间分布法的收敛速度和结果很好,而对于另外两种方法,基本不能收敛。如下:
b. 匹配:两个点集之间的点进行配对
匹配的策略有以下几种:
* 最邻近点法:此方法还可以应用k-d树或最邻近点缓存进行加速
* Normal shooting:点集P1中取一点,沿其点法向量,到点集P2(曲面的)的交点,形成一个点对
* 投影法:将源点集P1投影到目的点集P2上,沿着P2的相机的视角方向,又称“reverse calibration”,搜索度量方法包括点对点距离,点对线距离,密度,颜色等。
* 基于向量间角度或颜色的兼容度量方法(Compatibility metric)
Fast ICP中不考虑颜色,密度信息。
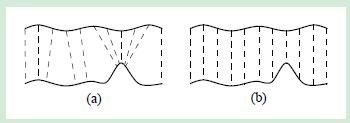
这里先给出投影法(b)与最近邻法(b)的示意图:
从图上看,可以看出最邻近点法容易受到噪声的干扰,而投影法不受噪声的干扰。
比较Normal shooting、最邻近点法和投影法三种方法:
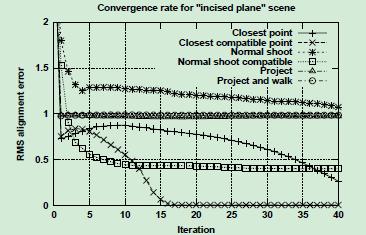
在雕刻十字面的场景下:
虽然最邻近点法容易受到噪声干扰,但对于特征比较少的场景下,最邻近点(兼容)法是唯一能完全收敛的方法。效果最好。对于投影法,收敛很快,但是效果不是很好。Normal shooting法在这两方面都表现平平。
对于复杂的草原场景,几种方法的收敛结果最终都基本相同,但其收敛速度和计算速度却有很大的差别:
从上图来看,投影法的计算速度非常快,这是因为不仅投影法的收敛速度快,而且其算法复杂度为O(1),而其他的算法复杂度为O(logN)。
c. 权重:给每个匹配的点对分配权重
权重分配的策略有以下几种:
* 均匀分配,即常数加权。
* 根据点对距离加权,点对间距大,权重就小,反之,权重就大。
* 根据向量的一致性(compability)进行加权,weight = n1 * n2
* 不确定性
这几种方法的收敛速度和效果都差别大。总体上来讲,向量一致(兼容)的方法 适应性和速度比其他方法好点。
d. 去除:去除不符合条件的点对
这个阶段的策略包括
* 固定阈值法:当间距大于一个值时,就去除这个点对
* 固定比例法:每次迭代,去除最差的%n的点对
* 标准差法:将阈值设置为所有点对间距的标准差*2.5
* 去除曲面边界的点对,如下图,曲面边界点的点对是不合理的,在两个点集做部分匹配的时候。
这几种方法的收敛速度差别不大,而且收敛效果也差别不大。但是去除outlier点对这个步骤 对收敛结果 的作用还是明显的。
e. 误差度量和最小化:基于以上点对,给出每个点对的误差计算方法
误差度量的策略:
* 点对的距离平方和
* 点到面的距离平方和
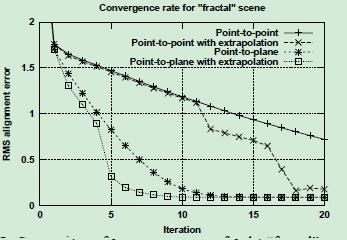
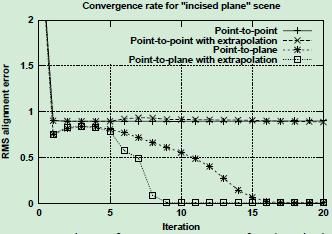
* 点到点和点到面的外推法
比较其收敛速率和效果,点到面和点到面外推法的度量方式效果更好。
Fast ICP分析了不同阶段里,各种因素或策略对算法性能和结果的影响。应可以根据不同的需求,来选取不同的算法对点集或曲面进行配准。
在算法效果差别不大的情况下,尽量选择简单的算法,来提高运行速度,如随机采样,常数加权,固定阈值等。
Fast ICP在网上有开源的代码,研究一下对此算法会有更深的理解。