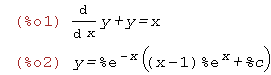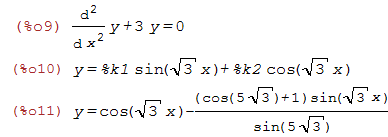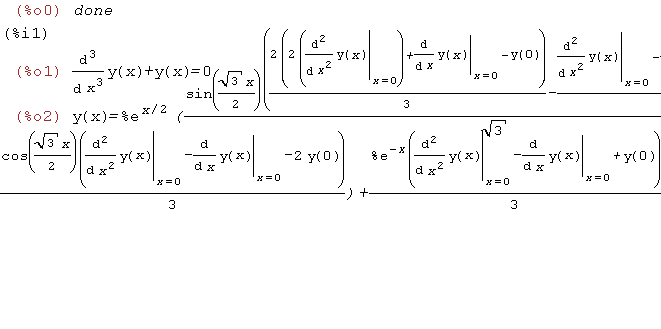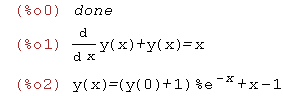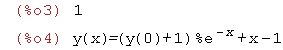使用Maxima求解常微分方程~

                                                                         使用Maxima求解常微分方程~

含带导数符号或带微分符号的未知函数的方程称为微分方程。
如果在微分方程中未知函数是一个变元的函数，这样的微分方程称为常微分方程。

1 一阶、二阶常微分方程的通解

Maxima 可以求解很多种类的常微分方程。
对于可以给出闭式解的一阶和二阶常微分方程，Maxima 会试图求出其精确解。
下面给出三个简单的例子。

(%i1)

eq1:'diff(y,x)+y=x; sol1:ode2(eq1,y,x);

 

 

(%i3)

eq2:'diff(y,x,2)+y=sin(3*x); sol2:ode2(eq2,y,x);

(%i5)

eq3:'diff(y,x,3)+y=0; sol3:ode2(eq3,y,x);

上面的例子用了ode2函数来求解常微分方程。
在定义方程时，微分函数diff之前有一个单引号（‘），这表示让Maxima只给出形式上的输出，并不真的进行计算。
这是因为我们这里只要列出方程，并不想让Maxima真的求导。
sol1 中的%c 和 sol2 中的 %k1 %k2 是任意常数。
ode2函数只能求解一阶和二阶常微分方程，第三个例子给出的是一个三阶常微分方程，无法求解，因此输出 false。

 

2 初值问题

函数ic1 (solution, xval, yval)和ic2 (solution, xval, yval, dval)分别用来解一阶和二阶微分方程的初值问题，其中solution是用ode2解得的通解，xval和yval分别是自变量和因变
量的初值，dval是因变量一阶导数的初值。

(%i7)

ic1(sol1,x=0,y=1);

(%i8)

ic2(sol2,x=0,y=1,'diff(y,x)=-1);

3 边值问题

函数bc2 (solution, xval_1, yval_1, xval_2, yval_2)用来求解二阶微分方程的边值问题，
其中solution是ode2解得的通解，xval_1、yval_1、xval_2和yval_2分别为自变量和因变量在第一点和第二点的取值。

(%i9)

eq4:'diff(y,x,2)+diff(y,x)/2+3*y=0; sol4:ode2(eq4,y,x); bc2(sol4,x=0,y=1,x=5,y=-1);

 

4 利用Laplace变换法求解常微分方程(组)

如果待求解的常微分方程(组)是线性常系数的。则可以利用Laplace变换法来求解。
Maxima 中也提供了相应的求解函数 desolve()，desolve()函数既可以求解ODE 方程，也可以求解ODE方程组。函数的基本形式如下。
desolve (eqn, y) 
desolve ([eqn_1, ..., eqn_n], [y_1, ..., y_n]) 
这里待解函数不能只写变量名（例如y），而需要明确写出对自变量的依赖关系（例如y(x)）。

下面是一个简单的例子：

(%i12)

kill(all); eq5:'diff(y(x),x,3)+y(x)=0; desolve(eq5,y(x));

如果初值是已知的，可以使用atvalue()命令来提供初值。
如果提供了足够的初值条件，再用的desolve()函数求解时积分常数自然就可以确定了。

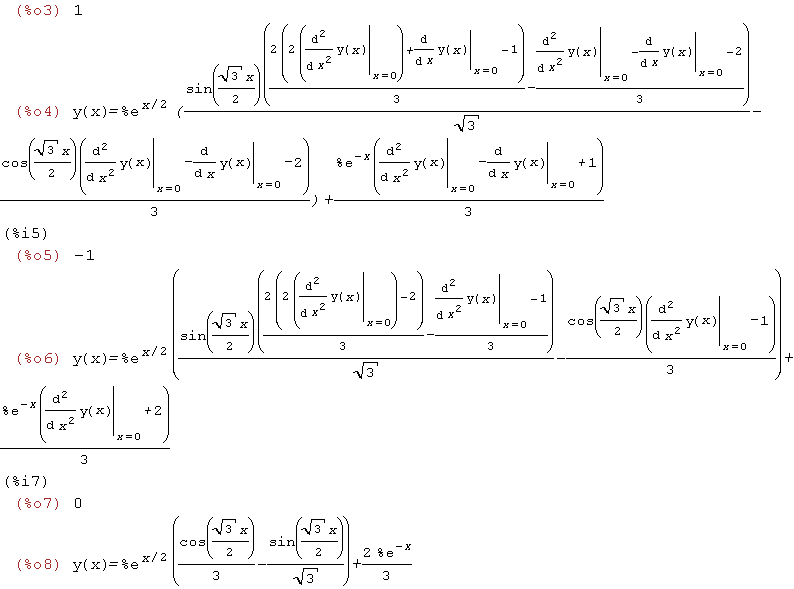
(%i3)

atvalue(y(x),x=0,1); desolve(eq5,y(x)); atvalue('diff(y(x),x),x=0,-1); desolve(eq5,y(x)); atvalue('diff(y(x),x,2),x=0,0); desolve(eq5,y(x));

下面给出一个常微分方程组求解的例子。

(%i9)

kill(all); eq6:'diff(f(x),x,2)+'diff(g(x),x)+3*f(x)=15*exp(-x); eq7:'diff(g(x),x,2)-4*'diff(f(x),x)+3*g(x)=16*sin(x); ode_syst:[eq6,eq7]; atvalue(f(x),x=0,35); atvalue('diff(f(x),x),x=0,-48); atvalue(g(x),x=0,27); atvalue('diff(g(x),x),x=0,-55); desolve(ode_syst,[f(x),g(x)]);

下面是试验部分。

(%i9)

kill(all); eq1:'diff(y(x),x)+y(x)=x; sol1:desolve(eq1,y(x));

(%i3)

atvalue(y(x),x=1,1); desolve(eq1,y(x));

(%i5)

ic1(y=(%c+1)*exp(-x)+x-1,x=1,y(x)=1);

说明 desolve 函数提供的初值必须是x=0 处的。
ic1 不能用来直接求解 desolve 函数的结果。必须要人为的处理一下结果的形式。这一点上确实不方便。