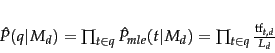语言模型
1. 对检索用户的通常建议是使用在文档中出现的词作为query,因此,如果一篇文章与查询词相关,那么这篇文章的模型可以生成这个query,因此检索模型从P(R = 1|q, d) 变为了P(q|Md),Md是文章的模型
2. 语言模型:
a. 形式语言,例如有限状态自动机,根据文法来产生语言
b. 不确定的状态的自动机,每一个状态可以以不同的概率产生不同的词或者结束
例如状态q1:
q1
P(STOP|q1) = 0.2
the 0.2
a 0.1
frog 0.01
toad 0.01
said 0.03
likes 0.02
that 0.04
. . . . . .
在这种情况下,产生一个字符串的概率为:
P(frog said that toad likes frog) = (0.01 ×0.03 × (12.2) 0.04 × 0.01 × 0.02 × 0.01)
×(0.8 ×0.8 × 0.8 × 0.8
这是没有考虑字符串顺序的情况,如果考虑顺序则应该是
P(t1t2t3t4) = P(t1)P(t2|t1)P((12.4) t3|t1t2)P(t4|t1t2t3)
或者只简化为马尔科夫链
P(t1t2t3t4) = P(t1)P(t2|t1)P(t3|t2)P(t4|t3) (二元语言模型)
但最简单的形式还是这些单词相互独立
Puni(t1t2t3t4) = P(t1)P(t2)P(t3)P(t4)
这个被称为一元语言模型
因此,在一个词的集合中,考虑长度为Ld的文档,tf1 个t1 组成,tf2 个t2组成... , 这样一篇文档被生成的概率即是多项式beinuli模型,概率为:
3. 对于一个给定的query,我们根据P(d|q) 来进行ranking
P(d|q) = P(q|d)P(d)/P(q)
p(q)对所有的文档都是一样的,因此可以忽略,p(d) 通常也进行了统一,因此只需要考虑p(q/d)
因此,从文档产生query变成了与从词典产生文档同样的问题,多项式一元语言模型
Kq = Ld!/(tft1,d!tft2,d! · · · tftM,d!)
如果简单地把p(t/Md) 定义为TFt,d / Ld ,则有如下公式:
但是query中会出现文档里没有的词,同时需要到各个词的出现频率进行平滑,因此公式更正为: