图像分割之（二）Graph Cut（图割）
上一文对主要的分割方法做了一个概述。那下面我们对其中几个比较感兴趣的算法做个学习。下面主要是Graph Cut，下一个博文我们再学习下Grab Cut，两者都是基于图论的分割方法。另外OpenCV实现了Grab Cut，具体的源码解读见博文更新。接触时间有限，若有错误，还望各位前辈指正，谢谢。
Graph cuts是一种十分有用和流行的能量优化算法，在计算机视觉领域普遍应用于前背景分割（Image segmentation）、立体视觉（stereo vision）、抠图（Image matting）等。
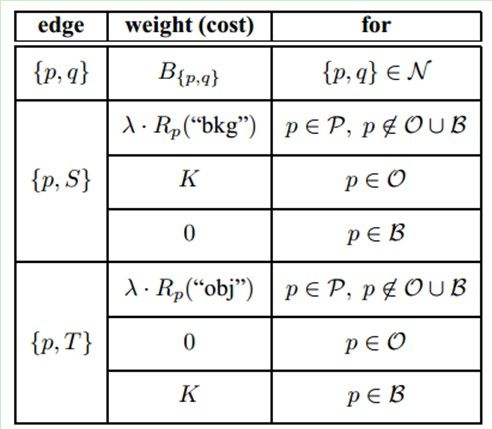
此类方法把图像分割问题与图的最小割（min cut）问题相关联。首先用一个无向图G=<V，E>表示要分割的图像，V和E分别是顶点（vertex）和边（edge）的集合。此处的Graph和普通的Graph稍有不同。普通的图由顶点和边构成，如果边的有方向的，这样的图被则称为有向图，否则为无向图，且边是有权值的，不同的边可以有不同的权值，分别代表不同的物理意义。而Graph Cuts图是在普通图的基础上多了2个顶点，这2个顶点分别用符号”S”和”T”表示，统称为终端顶点。其它所有的顶点都必须和这2个顶点相连形成边集合中的一部分。所以Graph Cuts中有两种顶点，也有两种边。
第一种顶点和边是：第一种普通顶点对应于图像中的每个像素。每两个邻域顶点（对应于图像中每两个邻域像素）的连接就是一条边。这种边也叫n-links。
第二种顶点和边是：除图像像素外，还有另外两个终端顶点，叫S（source：源点，取源头之意）和T（sink：汇点，取汇聚之意）。每个普通顶点和这2个终端顶点之间都有连接，组成第二种边。这种边也叫t-links。
上图就是一个图像对应的s-t图，每个像素对应图中的一个相应顶点，另外还有s和t两个顶点。上图有两种边，实线的边表示每两个邻域普通顶点连接的边n-links，虚线的边表示每个普通顶点与s和t连接的边t-links。在前后景分割中，s一般表示前景目标，t一般表示背景。
图中每条边都有一个非负的权值we，也可以理解为cost（代价或者费用）。一个cut（割）就是图中边集合E的一个子集C，那这个割的cost（表示为|C|）就是边子集C的所有边的权值的总和。
Graph Cuts中的Cuts是指这样一个边的集合，很显然这些边集合包括了上面2种边，该集合中所有边的断开会导致残留”S”和”T”图的分开，所以就称为“割”。如果一个割，它的边的所有权值之和最小，那么这个就称为最小割，也就是图割的结果。而福特-富克森定理表明，网路的最大流max flow与最小割min cut相等。所以由Boykov和Kolmogorov发明的max-flow/min-cut算法就可以用来获得s-t图的最小割。这个最小割把图的顶点划分为两个不相交的子集S和T，其中s ∈S，t∈ T和S∪T=V 。这两个子集就对应于图像的前景像素集和背景像素集，那就相当于完成了图像分割。
也就是说图中边的权值就决定了最后的分割结果，那么这些边的权值怎么确定呢？
图像分割可以看成pixel labeling（像素标记）问题，目标（s-node）的label设为1，背景（t-node）的label设为0，这个过程可以通过最小化图割来最小化能量函数得到。那很明显，发生在目标和背景的边界处的cut就是我们想要的（相当于把图像中背景和目标连接的地方割开，那就相当于把其分割了）。同时，这时候能量也应该是最小的。假设整幅图像的标签label（每个像素的label）为L= {l1,l2,,,, lp }，其中li为0（背景）或者1（目标）。那假设图像的分割为L时，图像的能量可以表示为：
E(L)=aR(L)+B(L)
其中，R(L)为区域项（regional term），B(L)为边界项（boundary term），而a就是区域项和边界项之间的重要因子，决定它们对能量的影响大小。如果a为0，那么就只考虑边界因素，不考虑区域因素。E(L)表示的是权值，即损失函数，也叫能量函数，图割的目标就是优化能量函数使其值达到最小。
区域项：
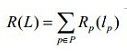，其中Rp(lp)表示为像素p分配标签lp的惩罚，Rp(lp)能量项的权值可以通过比较像素p的灰度和给定的目标和前景的灰度直方图来获得，换句话说就是像素p属于标签lp的概率，我希望像素p分配为其概率最大的标签lp，这时候我们希望能量最小，所以一般取概率的负对数值，故t-link的权值如下：
Rp(1) = -ln Pr(Ip|’obj’)； Rp(0) = -ln Pr(Ip|’bkg’)
由上面两个公式可以看到，当像素p的灰度值属于目标的概率Pr(Ip|’obj’)大于背景Pr(Ip|’bkg’)，那么Rp(1)就小于Rp(0)，也就是说当像素p更有可能属于目标时，将p归类为目标就会使能量R(L)小。那么，如果全部的像素都被正确划分为目标或者背景，那么这时候能量就是最小的。
边界项：
其中，p和q为邻域像素，边界平滑项主要体现分割L的边界属性，B<p,q>可以解析为像素p和q之间不连续的惩罚，一般来说如果p和q越相似（例如它们的灰度），那么B<p,q>越大，如果他们非常不同，那么B<p,q>就接近于0。换句话说，如果两邻域像素差别很小，那么它属于同一个目标或者同一背景的可能性就很大，如果他们的差别很大，那说明这两个像素很有可能处于目标和背景的边缘部分，则被分割开的可能性比较大，所以当两邻域像素差别越大，B<p,q>越小，即能量越小。
好了，现在我们来总结一下：我们目标是将一幅图像分为目标和背景两个不相交的部分，我们运用图分割技术来实现。首先，图由顶点和边来组成，边有权值。那我们需要构建一个图，这个图有两类顶点，两类边和两类权值。普通顶点由图像每个像素组成，然后每两个邻域像素之间存在一条边，它的权值由上面说的“边界平滑能量项”来决定。还有两个终端顶点s（目标）和t（背景），每个普通顶点和s都存在连接，也就是边，边的权值由“区域能量项”Rp(1)来决定，每个普通顶点和t连接的边的权值由“区域能量项”Rp(0)来决定。这样所有边的权值就可以确定了，也就是图就确定了。这时候，就可以通过min cut算法来找到最小的割，这个min cut就是权值和最小的边的集合，这些边的断开恰好可以使目标和背景被分割开，也就是min cut对应于能量的最小化。而min cut和图的max flow是等效的，故可以通过max flow算法来找到s-t图的min cut。目前的算法主要有：
1) Goldberg-Tarjan
2) Ford-Fulkerson
3) 上诉两种方法的改进算法
权值：
Graph cut的3x3图像分割示意图：我们取两个种子点（就是人为的指定分别属于目标和背景的两个像素点），然后我们建立一个图，图中边的粗细表示对应权值的大小，然后找到权值和最小的边的组合，也就是（c）中的cut，即完成了图像分割的功能。
上面具体的细节请参考：
《Interactive Graph Cuts for Optimal Boundary & Region Segmentation of Objects in N-D Images》（Boykov，iccv01）这篇paper讲怎么用graphcut来做image segmentation。
在Boykov 和 Kolmogorov 俩人的主页上就有大量的code。包括maxflow/min-cut、stereo algorithms等算法：
http://pub.ist.ac.at/~vnk/software.html
http://vision.csd.uwo.ca/code/
康奈尔大学的graphcuts研究主页也有不少信息：
http://www.cs.cornell.edu/~rdz/graphcuts.html
《Image Segmentation: A Survey of Graph-cut Methods》（Faliu Yi，ICSAI 2012）