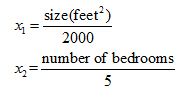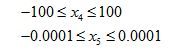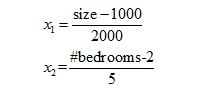Machine Learning - Gradient Descent in Practice
This article contains some skills in the implementation of Gradient Descent, including feature scaling, mean normalization and choosing learning rate.
Gradient descent in practice
1. Feature Scaling
Feature Scaling
Idea: Make sure features are on a similar scale, so the gradient descent will converge much faster.
E.g. x1 = size (0-2000 feet2)
x2 = number of bedrooms (1-5)
Get every feature into approximately a -1≤ xi ≤1 range.
These ranges are ok:
These ranges are not good
Mean normalization
Replace xi with xi -μi to make features have approximately zero mean (Do not apply tox0 =1). Where μiis the mean value of feature i.
E.g.
2. Learning rate
Gradient descent
- “Debugging”: How to make sure gradient descent is working correctly.
- How to choose learning rate α .
Making sure gradient descent is working correctly.
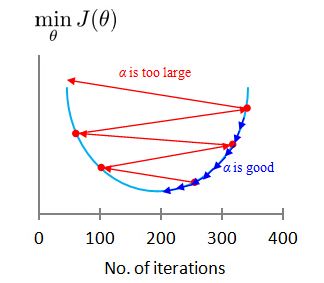
- J(θ) should decrease every iteration.
Example automatic convergence test:
Declare convergence if J(θ) decreases by less than 10-3 in one iteration.
- Gradient descent not working: Use smaller α.
- For sufficiently small α , J(θ) should decrease on every iteration.
- But if α is too small, gradient descent can be slow to converge.
Summary:
- If α is too small: slow convergence.
- If α is too large: J(θ) may not decrease on every iteration; may not converge.
To choose α, try: ...,0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, ...
3. Matlab Code of Gradient descent with Multiple Variables
function [theta, J_history] = gradientDescentMulti(X, y, theta, alpha, num_iters)
//% X is the training data (design matrix)
//% y is the label of training data (in vector)
//% theta is the vector of parameters
//% alpha is the learning rate
//% num_iters is the number of iterations
//% Initialize some values
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);
for iter = 1:num_iters
//% Perform a single gradient step on the parameter vector theta.
for i = 1:size(X,2)
theta_tmp(i) = theta(i) - alpha*(sum((X*theta-y).*X(:,i)))/m;
end
theta = theta_tmp';
//% Save the cost J in every iteration
J_history(iter) = computeCostMulti(X, y, theta); //% compute J(theta)
end
end
function J = computeCostMulti(X, y, theta) //% COMPUTECOSTMULTI Compute cost for linear regression with multiple variables //% Initialize some useful values m = length(y); % number of training examples J = 0; //% Compute the cost of a particular choice of theta J = 0.5*(X*theta-y)'*(X*theta-y)/m; end