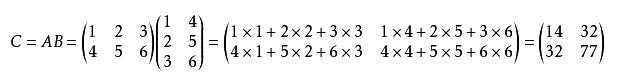Data Science from Scratch 之 MapReduce
MapReduce
MapReduce是一种计算模型,只不过这种计算模型是在并行计算世界里。
考虑一个简单的例子-单词统计
from collections import Counter
import re
documents = ["data science", "big data", "science fiction"]
def tokenize(message):
message = message.lower()
all_words = re.findall('[a-z0-9]+',message)
return set(all_words)
def word_count_old(documents):
return Counter(word for document in documents
for word in tokenize(document))
print word_count_old(documents)
最简单的统计是这样的,但如果有成千上亿个这样的文档,这个方法就显得特别慢了,还有可能电脑吃不消那么大的数据。
先贴上代码:
def wc_mapper(document):
"""for each word in the document,emit (word,1)"""
for word in tokenize(document):
yield (word,1)
def wc_reducer(word,counts):
yield (word,sum(counts))
def word_count(documents):
collector = defaultdict(list)
for document in documents:
for word,count in wc_mapper(document):
collector[word].append(count)
print collector
return [output for word,counts in collector.iteritems() for output in wc_reducer(word,counts)]
print word_count(documents)
这部分难以理解,我们一步一步来看。就以documents = ["data science", "big data", "science fiction"]为例,
首先,将documents传入word_count函数,开始定义了一个key-value的变量,只不过这里的变量key为单词,value是列表形式。当执行wc_mapper函数时,只要有一个单词,我就产出(word,1)东西出来,因此当
for document in documents:
for word,count in wc_mapper(document):
collector[word].append(count)
这段代码执行完之后,collector里面的内容是:
{'science': [1, 1], 'fiction': [1], 'data': [1, 1], 'big': [1]}
接下来执行wc_reducer函数,key不变,value统计起来。最后输出
[('science', 2), ('fiction', 1), ('data', 2), ('big', 1)]
没有想到听起来高大上的MapReduce算法这么简单。
为什么选择MapReduce?
MapReduce计算模型能够允许我们分布式计算。
一般化的,我们想要这个模型易用:
def map_reduce(inputs,mapper,reducer):
collector = defaultdict(list)
for input in inputs:
for key,value in mapper(input):
collector[key].append(value)
return [output
for key,values in collector.iteritems()
for output in reducer(key,values)]
print map_reduce(documents,wc_mapper,wc_reducer)
但是,map和reducer需要改一下
def reduce_values_using(fn,key,values):
yield (key,fn(values))
def values_reducer(fn):#fn为聚合函数
return partial(reduce_values_using,fn)
count_distinct_reducer = values_reducer(sum)
count_distinct_reducer = values_reducer(lambda values:len(set(values)))
print map_reduce(documents,wc_mapper,count_distinct_reducer)
状态分析
假设有这样的情况,我们想分析一个星期中那一天人们谈论数据科学最多,为了找到这个,我们只需要找到数据科学这个词在每天中出现的次数。
def data_science_day_mapper(status_update):
if 'data science' in status_update['text'].lower():
day_of_week = status_update['created_at'].weekday()
yield (day_of_week,1)
data_science_days = map_reduce(status_updates,data_science_day_mapper,sum_reducer)
print data_science_days
矩阵乘法
矩阵乘法,看到这篇文章的人都上大学,并都会矩阵乘法的,给一个m*n的矩阵A,和n*k的矩阵B,相乘得到的矩阵C中的第i行第j列的元素是A矩阵i行所有元素分别于B中的第j列相乘并相加得到。如果矩阵特别稀疏,我们可以用一个元组(name,i,j,value)来表示矩阵name中的第i行第j列元素value,当然这个元素的值value是非0的。我们可以设计MapReduce来求解这样的问题。
看了这部分内容看了2个小时,终于理解了,衰。还是自己脑子不够好啊。前方预警,请系好安全带。。。
我们先来分析一下基本矩阵乘法是怎么样的?
是这样的哇,如果你还不懂,去补补数学吧。
刚才我们也说了,在大数据中,矩阵一般为稀疏的,所以我们考虑这样的矩阵。
A=[[3,2,1],
[0,0,0]]
B=[[4,-1,0],
[10,0,0],
[0,0,0]]
相乘以后的结果为
32 -3 0
0 0 0
我们现在来分析一下怎么用mapreduce来求解。
这是一个2*3与3*3的矩阵相乘,得到的结果是2*3的。比如结果中(0,0)元素32是3*4+2*10+1*0得到的,而且我们计算整个流程,发现A中(0,0)这个元素计算了3次,分别在计算C中元素(0,0),(0,1),(0,2)中用到。类似地,B也一样,只不过B是按列来的。所以下面的代码是这样的:
def matrix_multiply_mapper(m,element):
#element是一个4元组,name是矩阵标志,i,j是坐标,value是值
name,i,j,value = element
if name=='A':
for k in range(m):
# print ((i,k),(j,value))
yield ((i,k),(j,value)) #前面的(i,k)为key,表示在接下来计算结果的时候用到,将参与计算Cik的坐标,j表示参与计算向量的第几个坐标,下面还会讲
else:
for k in range(m):
# print ((k,j),(i,value))
yield ((k,j),(i,value))
得到了这样的map,我们看看结果
(0, 1): [(0, 3), (1, 2), (0, -1)],
(0, 0): [(0, 3),(1, 2), (0, 4), (1, 10)],
(2, 1): [(0, -1)],
(1, 1): [(0, -1)],
(2, 0): [(0, 4),(1, 10)],
(1, 0): [(0, 4), (1, 10)],
(0, 2): [(0, 3), (1, 2)]})
这样的表示有什么意义呢,比如第一行,表示结果矩阵中(0,1)这个元素由后面的列表计算得到,那怎么计算呢,这是reduce的工作了。
def matrix_multiply_reducer(m,key,indexed_values):
results_by_index = defaultdict(list)
for index,value in indexed_values:
print index,value
results_by_index[index].append(value)
print results_by_index
sum_product = sum(results[0]*results[1]
for results in results_by_index.values()
if len(results)==2)
if sum_product != 0.0:
yield (key,sum_product)
def map_reduce(inputs,mapper,reducer):
collector = defaultdict(list)
for input in inputs:
for key,value in mapper(input):
collector[key].append(value)
# print collector
return [output
for key,values in collector.iteritems()
for output in reducer(key,values)]
就拿计算结果的第一个元素来说吧,我们得到的结果是这样的
(0, 1): [(0, 3), (1, 2), (0, -1)],
表示结果矩阵中(0,1)这个位置元素由后面的数值计算而成,在reduce中,传过来的是values是
[(0, 3), (1, 2), (0, -1)]
我们得到了这样的 {0: [3, -1], 1: [2]}),有没有感觉,不错,二元组中前面的为key,后面的为值,表示是同一的,然后计算3*-1=-3,也就是(0,1)这个位置了,那我们有疑问了,那2呢,因为2只有一个,其他没有的都是0,所以结果相加得到的为2。
这部分内容,真的特别有用,要好好消化。
上帝真的很注意细节!