蓝桥杯 矩形区域的交和并 计算几何

    在编写图形界面软件的时候，经常会遇到处理两个矩形的关系。


    如图【1.jpg】所示，矩形的交集指的是：两个矩形重叠区的矩形，当然也可能不存在（参看【2.jpg】）。两个矩形的并集指的是：能包含这两个矩形的最小矩形，它一定是存在的。


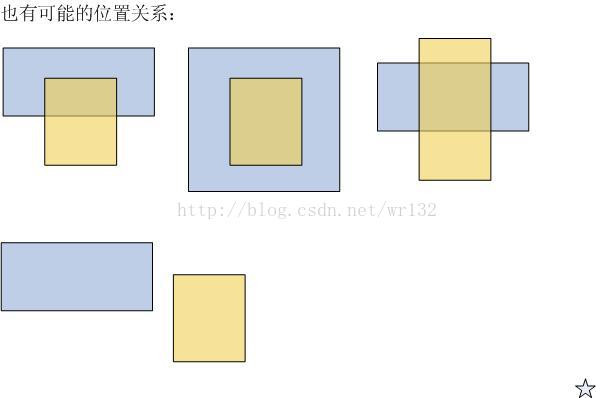
    本题目的要求就是：由用户输入两个矩形的坐标，程序输出它们的交集和并集矩形。


    矩形坐标的输入格式是输入两个对角点坐标，注意，不保证是哪个对角，也不保证顺序（你可以体会一下，在桌面上拖动鼠标拉矩形，4个方向都可以的）。


    输入数据格式：
x1,y1,x2,y2
x1,y1,x2,y2
    
    数据共两行，每行表示一个矩形。每行是两个点的坐标。x坐标在左，y坐标在右。坐标系统是：屏幕左上角为(0,0)，x坐标水平向右增大；y坐标垂直向下增大。


    要求程序输出格式：
x1,y1,长度,高度
x1,y1,长度,高度


    也是两行数据，分别表示交集和并集。如果交集不存在，则输出“不存在”


    前边两项是左上角的坐标。后边是矩形的长度和高度。


    例如，用户输入：
100,220,300,100
150,150,300,300


    则程序输出：
150,150,150,70
100,100,200,200


    例如，用户输入：
10,10,20,20
30,30,40,40


    则程序输出：
不存在
10,10,30,30




    注意：


    请仔细调试！您的程序只有能运行出正确结果的时候才有机会得分！
    

    在评卷时使用的输入数据与试卷中给出的实例数据可能是不同的。

题目中给出的两个矩形的对角点的参数，这两个对角点到底是哪条对角线的点不确定，其实也不重要。讨论两个矩形的交集和并集，这两个概念图片中给出的很清楚，下面，分析一下这道题目的做法：

预处理的工作，比较蛋疼的是，题目中给出的四个参数并不是标准的数值，而是一个掺杂了“，”的字符串，我们要从字符串中提取出四个数值，然后将两个矩形的所有x值放在一起，所有的y值放在一起，方便之后处理

一、交集

      在求交集的时候，我们可以使用扫描线法，不难发现，如果两个矩形相交，我们从左向右扫描x值，第二个x值就是重叠部分矩形的左上角顶点的x值；从上到下扫描，第二个遇到的y值就是重叠部分矩形的左上角顶点的y值，这样，我们就得到了左上角顶点坐标。然后，我们再扫描一遍x，可以看到，第二个x和第三个x的差的绝对值就是重叠矩形的宽度；再扫描一遍y，第二个y和第三个y的差的绝对值就是重叠矩形的高度。

     ok，思路很清楚，从图形上也很直观，关键是如何扫描，这里就可以看到我们之前将x和y分别单独存储在一起的好处，x[]数组中存储了两个矩形的4个x值，y[]数组中存储了两个矩形的4个y值，我们对x[]和y[]分别进行从小到大排序，这样从左到右的四个值正好与我们的扫描顺序相对应，也就是直接把相应的数据代入即可

    关于判断两个矩形是否相交，有很多方法，这里，我使用了一种比较好想的，我们首先要算出两个矩形的宽度w1，w2和高度h1，h2，然后对x[]和y[]进行从小到大排序，将两个矩形看成一个图形，求出这个图形的宽度w=(x[3]-x[0])和高度h=(y[3]-y[0])，如果w>=w1+w2或者h>=h1+h2，那两个图形肯定是不相交的。

二、并集

            这个比较简单，因为上一步已经排好序了，所以这一步直接找第一个遇到的x值和第一个遇到的y值作为左上角顶点的坐标，宽度就是x的最大值-最小值，高度就是y的最大值-最小值

#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;

struct Rec
{
	int x1,y1;
	int x2,y2;
}rec[2];

void getArg(char *str,char *num,int *arg)
{
	int i,j,p,temp,q;
	q=0;
	for(i=0;i<strlen(str);i++)
	{
		if(str[i]>='0'&&str[i]<='9')
		{
			p=0;
			temp=0;
			for(;str[i]!=','&&i<strlen(str);i++)
			{
				num[p++]=str[i];
			}
			for(j=p-1;j>=0;j--)
			{
				temp+=(int)(num[j]-'0')*pow(10.0,p-j-1);
			}
			arg[q++]=temp;
		}
	}
}

bool judge(int *x,int *y)
{
	int w1,w2,h1,h2;
	int max_x,min_x,max_y,min_y;
	w1=abs(x[0]-x[1]);
	w2=abs(x[2]-x[3]);
	h1=abs(y[0]-y[1]);
	h2=abs(y[2]-y[3]);
	sort(x,x+4);
	sort(y,y+4);
	min_x=x[0];
	max_x=x[3];
	min_y=y[0];
	max_y=y[3];
	if(max_x-min_x>=w1+w2)
	return 1;
	if(max_y-min_y>=h1+h2)
	return 1;
	return 0;
	
}

void jiaoji(int *x,int *y)
{
	if(judge(x,y))
	{
		cout<<"不存在"<<endl;
		return;
	}
	int x1,y1,h,w;
	
	w=abs(x[1]-x[2]);
	h=abs(y[1]-y[2]);
	x1=x[1];
	y1=y[1];
	cout<<x1<<','<<y1<<','<<w<<','<<h<<endl;
}

void bingji(int *x,int *y)
{
	int x1,y1,h,w;
	w=x[3]-x[0];
	h=y[3]-y[0];
	x1=x[0];
	y1=y[0];
	cout<<x1<<','<<y1<<','<<w<<','<<h<<endl;
}


int main()
{
	int arg[4],i,j,p;
	int temp;
	int x[4],y[4];
	char str[100],num[10];
	p=0;
	for(i=0;i<2;i++)
	{
		cin>>str;
		getArg(str,num,arg);
		x[p++]=arg[0];
		y[p-1]=arg[1];
		x[p++]=arg[2];
		y[p-1]=arg[3];
	}
	jiaoji(x,y);
	bingji(x,y);
	return 0;
}