坐在马桶上看算法:Dijkstra最短路算法
2014-04-01 09:17:52

上周我们介绍了神奇的只有五行的Floyd最短路算法,它可以方便的求得任意两点的最短路径,这称为“多源最短路”。本周来来介绍指定一个点(源点)到其余各个顶点的最短路径,也叫做“单源最短路径”。例如求下图中的1号顶点到2、3、4、5、6号顶点的最短路径。
与Floyd-Warshall算法一样这里仍然使用二维数组e来存储顶点之间边的关系,初始值如下。
我们还需要用一个一维数组dis来存储1号顶点到其余各个顶点的初始路程,如下。
我们将此时dis数组中的值称为最短路的“估计值”。
既然是求1号顶点到其余各个顶点的最短路程,那就先找一个离1号顶点最近的顶点。通过数组dis可知当前离1号顶点最近是2号顶点。当选择了2号顶点后,dis[2]的值就已经从“估计值”变为了“确定值”,即1号顶点到2号顶点的最短路程就是当前dis[2]值。为什么呢?你想啊,目前离1号顶点最近的是2号顶点,并且这个图所有的边都是正数,那么肯定不可能通过第三个顶点中转,使得1号顶点到2号顶点的路程进一步缩短了。因为1号顶点到其它顶点的路程肯定没有1号到2号顶点短,对吧O(∩_∩)O~
既然选了2号顶点,接下来再来看2号顶点有哪些出边呢。有2->3和2->4这两条边。先讨论通过2->3这条边能否让1号顶点到3号顶点的路程变短。也就是说现在来比较dis[3]和dis[2]+e[2][3]的大小。其中dis[3]表示1号顶点到3号顶点的路程。dis[2]+e[2][3]中dis[2]表示1号顶点到2号顶点的路程,e[2][3]表示2->3这条边。所以dis[2]+e[2][3]就表示从1号顶点先到2号顶点,再通过2->3这条边,到达3号顶点的路程。
我们发现dis[3]=12,dis[2]+e[2][3]=1+9=10,dis[3]>dis[2]+e[2][3],因此dis[3]要更新为10。这个过程有个专业术语叫做“松弛”。即1号顶点到3号顶点的路程即dis[3],通过2->3这条边松弛成功。这便是Dijkstra算法的主要思想:通过“边”来松弛1号顶点到其余各个顶点的路程。
同理通过2->4(e[2][4]),可以将dis[4]的值从∞松弛为4(dis[4]初始为∞,dis[2]+e[2][4]=1+3=4,dis[4]>dis[2]+e[2][4],因此dis[4]要更新为4)。
刚才我们对2号顶点所有的出边进行了松弛。松弛完毕之后dis数组为:
接下来,继续在剩下的3、4、5和6号顶点中,选出离1号顶点最近的顶点。通过上面更新过dis数组,当前离1号顶点最近是4号顶点。此时,dis[4]的值已经从“估计值”变为了“确定值”。下面继续对4号顶点的所有出边(4->3,4->5和4->6)用刚才的方法进行松弛。松弛完毕之后dis数组为:
继续在剩下的3、5和6号顶点中,选出离1号顶点最近的顶点,这次选择3号顶点。此时,dis[3]的值已经从“估计值”变为了“确定值”。对3号顶点的所有出边(3->5)进行松弛。松弛完毕之后dis数组为:
继续在剩下的5和6号顶点中,选出离1号顶点最近的顶点,这次选择5号顶点。此时,dis[5]的值已经从“估计值”变为了“确定值”。对5号顶点的所有出边(5->4)进行松弛。松弛完毕之后dis数组为:
最后对6号顶点所有点出边进行松弛。因为这个例子中6号顶点没有出边,因此不用处理。到此,dis数组中所有的值都已经从“估计值”变为了“确定值”。
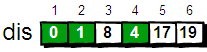
最终dis数组如下,这便是1号顶点到其余各个顶点的最短路径。
OK,现在来总结一下刚才的算法。算法的基本思想是:每次找到离源点(上面例子的源点就是1号顶点)最近的一个顶点,然后以该顶点为中心进行扩展,最终得到源点到其余所有点的最短路径。基本步骤如下:
-
将所有的顶点分为两部分:已知最短路程的顶点集合P和未知最短路径的顶点集合Q。最开始,已知最短路径的顶点集合P中只有源点一个顶点。我们这里用一个book[ i ]数组来记录哪些点在集合P中。例如对于某个顶点i,如果book[ i ]为1则表示这个顶点在集合P中,如果book[ i ]为0则表示这个顶点在集合Q中。
-
设置源点s到自己的最短路径为0即dis=0。若存在源点有能直接到达的顶点i,则把dis[ i ]设为e[s][ i ]。同时把所有其它(源点不能直接到达的)顶点的最短路径为设为∞。
-
在集合Q的所有顶点中选择一个离源点s最近的顶点u(即dis[u]最小)加入到集合P。并考察所有以点u为起点的边,对每一条边进行松弛操作。例如存在一条从u到v的边,那么可以通过将边u->v添加到尾部来拓展一条从s到v的路径,这条路径的长度是dis[u]+e[u][v]。如果这个值比目前已知的dis[v]的值要小,我们可以用新值来替代当前dis[v]中的值。
-
重复第3步,如果集合Q为空,算法结束。最终dis数组中的值就是源点到所有顶点的最短路径。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
|
#include <stdio.h>
int
main()
{
int
e[10][10],dis[10],book[10],i,j,n,m,t1,t2,t3,u,v,min;
int
inf=99999999;
//用inf(infinity的缩写)存储一个我们认为的正无穷值
//读入n和m,n表示顶点个数,m表示边的条数
scanf
(
"%d %d"
,&n,&m);
//初始化
for
(i=1;i<=n;i++)
for
(j=1;j<=n;j++)
if
(i==j) e[i][j]=0;
else
e[i][j]=inf;
//读入边
for
(i=1;i<=m;i++)
{
scanf
(
"%d %d %d"
,&t1,&t2,&t3);
e[t1][t2]=t3;
}
//初始化dis数组,这里是1号顶点到其余各个顶点的初始路程
for
(i=1;i<=n;i++)
dis[i]=e[1][i];
//book数组初始化
for
(i=1;i<=n;i++)
book[i]=0;
book[1]=1;
//Dijkstra算法核心语句
for
(i=1;i<=n-1;i++)
{
//找到离1号顶点最近的顶点
min=inf;
for
(j=1;j<=n;j++)
{
if
(book[j]==0 && dis[j]<min)
{
min=dis[j];
u=j;
}
}
book[u]=1;
for
(v=1;v<=n;v++)
{
if
(e[u][v]<inf)
{
if
(dis[v]>dis[u]+e[u][v])
dis[v]=dis[u]+e[u][v];
}
}
}
//输出最终的结果
for
(i=1;i<=n;i++)
printf
(
"%d "
,dis[i]);
getchar
();
getchar
();
return
0;
}
|
可以输入以下数据进行验证。第一行两个整数n m。n表示顶点个数(顶点编号为1~n),m表示边的条数。接下来m行表示,每行有3个数x y z。表示顶点x到顶点y边的权值为z。
|
1
2
3
4
5
6
7
8
9
10
|
6 9
1 2 1
1 3 12
2 3 9
2 4 3
3 5 5
4 3 4
4 5 13
4 6 15
5 6 4
|
运行结果是
|
1
|
0 1 8 4 13 17
|