动态规划入门,基础
在学习动态规划之前,请先熟悉深度优先搜索(DFS)。由于为新博客,所以烦劳先自行寻找资料学习DFS,过几日我会添加学习DFS的文章。
动态规划(DP)本是运筹学的一个分支,因此也是许多ACMer胸口永远的痛。什么是动态规划与其性质我在此不再进行说明,关于它的解释百度一下一大把。附上百度链接:点击打开链接
适用条件(看不懂可先跳过,之后我都会举例说明)
为什么动态规划如此让人头疼呢?我以从初学者过来的经验可以告诉大家,且结为下面两点。(个人理解,轻喷)
①状态?啥叫状态啊?这题状态怎么表示好啊?
②转移?这状态怎么转移?这状态还能转移?!!
不错,DP最难的两点便是状态的确定与转移。好了,废话不多说,下面我将结合趣味例题与大家分享。
例题1:
这里我们仍以大部分书上第一个例题数字三角形为例,将它改一改,相信都能看懂。
图1 图2
小明非常爱玩LOL,有一天,他来到了召唤师峡谷准备大干一场,可是这一次的召唤师峡谷却是三角形的(如图1,2),小明的出生点位于图中最上面的点,为了掀翻召唤师峡谷,小明决定收集更多的炸弹,图中数字代表此地炸弹个数,且小明只能一直往下走,每次只能往左下或者右下角的一处走,正确与错误走法如下:
(确实是画得很丑。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。那你还看?)
给出你一个图,请你编写一个程序帮小明计算出小明最多可以收集多少炸弹(别担心,小明的袋子是屎做的,装得下)。
走图1时,有些同学产生了一个感觉,“这TMD用贪心不就好了?”,然后请你看看图2这时再用贪心还行吗?
相信对深度优先搜索已经有了一定认识的同学,一眼就能看出来并喊道:“这个还不简单?一遍DFS就能出来!博主你拿这么水的题来唬我?”
好,那我们就先用DFS来求出结果。 为了方便,我们将所求最大值称为叶良辰值,对于某点(x,y)我们将其左下表示为(x+1,y),右下表示为(x+1,y+1),在这里我将只给出DFS的代码:点击查看代码
在代码中,我们将每一个dfs(i,j)当成(i,j)为起点的叶良辰值,这便是上面(上面你跳过的~~)所说的最优子结构。而当dfs(i+1,j)求出来后,并不会影响dfs(i,j)的求值,这便是无后效性。而每一对确定i,j都代表了一种状态。而根据dfs(x , y)=max(dfs(x + 1, y), dfs(x + 1, y + 1)) + map[x][y](怎么来的?请耐心往下看)来求出状态dfs(x,y),我们称其为状态转移方程式(原来如此哦)
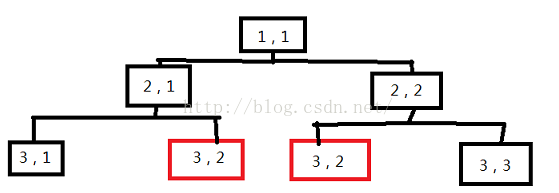
经过调试我们发现结果没有错误,可tmd居然超时了,怎么回事?下面请看看这个图:
(怎么样,这图还行吧!?)
通过观察发现在求dfs(2,1)与dfs(2,2)时,都会递归进入dfs(3,2),由此造成了重复的不必要的计算,当数据一大重复计算的将占绝大部分,这便是(上面你跳过的~~)子问题的重叠性(到这里我们对5个名词的概念进行了说明了,还不懂?~~~~退坑吧!!决策将在下面给出说明)。重复计算怎么解决?
既然会重复计算,那我们为什么不再计算过dfs(3,2)后保存下这个值呢?
于是我们可以写出如下代码:点击查看代码 我们称其为 记忆化搜索
不对啊?讲了这么久这么讲了记忆化搜索却不讲动态规划啊? 别急,记忆化搜索是利用动态规划求解的一种方式。下面我将介绍动态规划的另一种写法:递推
我们以dp[i][j]来表示以dp[i][j]为起点的叶良辰值,那么问题来了,怎么求?
第一步:确定状态:dp[i][j]:表示以dp[i][j]为起点的叶良辰值
第二步:做出决策:尝试左下/右下方走(决策一定要包含所以可能,在此表现为左或右)
第三步:状态转移:根据决策来建立状态转移方程:
若往左下走则 dfs(x , y)=dfs(x + 1, y) + map[x][y],因为往左下走,所以炸弹数一定为(x + 1, y)为起点的叶良辰值再加上在(x , y)可以捡到的炸弹数map[x][y]
若往右下走则同理 dfs(x , y)=dfs(x + 1, y + 1) + map[x][y]
所以最终取最大值状态转移方程便出来了 dfs(x , y)=max(dfs(x + 1, y), dfs(x + 1, y + 1)) + map[x][y]
~~这次不偷懒了,附上完整代码:对了!在这里先给读者留下一个疑问,代码中给出的为dp为一维数组而非二维,却仍然可以求出正确结果!不信可以去POJ-3176提交试试 点击查看完整代码
此问题我们将在下一次更新时给大家讲解!也可以自己先仔细想一想!望有帮助!谢谢支持!