JZOJ 1503.体育场

Description

　　观众席每一行构成一个圆形，每个圆形由300个座位组成，对300个座位按照顺时针编号1到300,且可以认为有无数多行。现在比赛的组织者希望观众进入场地的顺序可以更加的有趣，在门票上并没有规定每个人的座位，而是与这个圈中某个人的相对位置，可以坐在任意一行。
　　门票上标示的形式如下：A B x 表示第B个人必须在A的顺时针方向x个位置（比如A坐在4号位子，x=2，则B必须坐在6号位子）。
　　现在你就座位志愿者在入场口检票。如果拿到一张门票，与之前给定的矛盾，则被视为是假票，如果无矛盾，视为真票。现在给定该行入场观众的顺序，以及他们手中的门票，请问其中有多少假票？

Input

第一行两个数n(1<=n<=50,000)和m(1<=m<=100,000)。
接下来m行，每行三个数A，B，x标示B必须坐在A的顺时针方向x个位置。(1<=A<=N), B(1<=B<=N), X(0<=X<300) (A!=B)
以上字母含义如题所述。

Output

仅一个数，表示在m张票中有多少假票。

Sample Input

10 10
1 2 150
3 4 200
1 5 270
2 6 200
6 5 80
4 7 150
8 9 100
4 8 50
1 7 100
9 2 100

Sample Output

2

Data Constraint

Explain

　　第5张和第10张是假票

Constraint

　　对于20%的数据：n<=100
　　对于100%的数据：n<=50000

Solution

一看到这题，我就想到是并查集。如果读入一张新的票的信息，并且两个点不在一个点集中，则连一条边。设F[o]表示他的父亲是谁，Dis[o]表示他与他父亲的间隔距。假票的情况是当指针指向同一个点，但现距离与之前的距离不一样。

那么当两个点不在一个点集中时，如何计算他的距离呢？

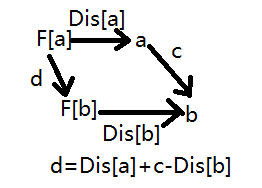
那么如何求点与点之间的距离呢？——我们就要压缩路径
我们先找到点o的祖先zxo，再算zxo的儿子与zxo的距离，再一层层递归下来。自己到祖先的距离为自己到父亲的距离+父亲到祖先的距离。
所以dis[o]=dis[o]+dis[f[o]]
核心代码：

function get(n:longint):longint;
begin
    if f[n]=n then exit(n) else
    begin
        get:=get(f[n]);
        dis[n]:=(dis[n]+dis[f[n]])mod 300;
        f[n]:=get;
    end;
end;

Code

const mo=300;
var f,dis:array[0..50000] of longint;
    i,j,k,l,n,m,x,y,z,xx,yy,ans:longint;
function get(n:longint):longint;
begin
    if f[n]=n then exit(n) else
    begin
        get:=get(f[n]);//压缩路径
        dis[n]:=(dis[n]+dis[f[n]])mod mo;
        f[n]:=get;
    end;
end;
begin
    readln(n,m);
    for i:=1 to n do f[i]:=i;
    for i:=1 to m do
    begin
        readln(x,y,z);
        xx:=get(x);
        yy:=get(y);
        if xx<>yy then
        begin
            f[yy]:=xx;
            dis[yy]:=(dis[x]+z-dis[y]+300)mod 300;
        end else
        if (dis[x]+z)mod 300<>dis[y] then inc(ans);
    end;
    writeln(ans);
end.

Special

通过这题我学会了压缩路径，且解决了数组模拟链表带来的时间超限问题。
时间超限30分的代码：

const mo=300;
var head,next,go,v,deep:array[0..100000] of longint;
    a,f:array[0..50000] of longint;
    i,j,k,l,n,m,x,y,xx,yy,z,tot,t,w,now,ans:longint;
procedure lb(x,y,z:longint);
begin
    inc(tot);
    next[tot]:=head[x];
    head[x]:=tot;
    go[tot]:=y;
    v[tot]:=z;
end;
function get(n:longint):longint;
begin
    if f[n]=n then exit(n) else
    begin
        f[n]:=get(f[n]);
        exit(f[n]);
    end;
end;
procedure bs(x,y:longint);
var i:longint;
begin
    i:=head[x];
    deep[x]:=y;
    while i<>0 do
    begin
        if deep[go[i]]=0 then
        begin
            a[go[i]]:=(a[x]+v[i])mod mo;
            bs(go[i],y+1);
        end;
        i:=next[i];
    end;
end;
begin
    readln(n,m);
    for i:=1 to n do f[i]:=i;
    for i:=1 to m do
    begin
        readln(x,y,z);
        xx:=get(x);
        yy:=get(y);
        if xx<>yy then
        begin
            f[yy]:=xx;
            lb(x,y,z);
            lb(y,x,300-z);
        end else
        begin
            fillchar(a,sizeof(a),0);
            fillchar(deep,sizeof(deep),0);
            bs(xx,0);
            if (a[y] mod mo<>(a[x]+z)) then inc(ans);
        end;
    end;
    writeln(ans);
end.

——2016.2.18 By Wzy