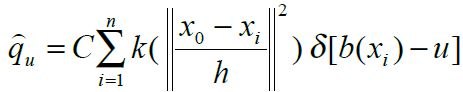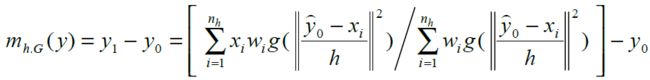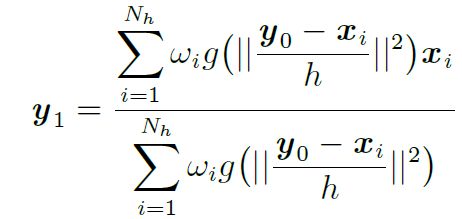基于mean shift的目标跟踪算法
Mean shift 算法是一种半自动跟踪方法在起始跟踪帧通过手工确定搜索窗口来选择运动目标计算核函数加权下的搜索窗口的直方图分布用同样的方法计算当前帧对应窗口的直方图分布以两个分布的相似性最大为原则使搜索窗口沿密度增加最大的方向移动目标的真实位置。
加权直方图
传统直方图仅仅统计落入直方图区间的像素的个数,而加权直方图进一步考虑了像素与目标中心的距离,远离目标中心的像素对直方图的贡献较小。
带空间位置信息的加权直方图的思想就是:在计算直方图时,给每个点赋予一定的权值,权值的大小根据它离中心点的远近,可以用高斯核函数或Epanechnikov Kernal来调节。常用的核密度函数有EpanechnikovKernal:
在统计颜色级的分布情况时,对每一个像素,根据它离窗口中心点的距离大小,赋予它一定的权值。当它离中心点越近时,它的权值越大,反之越小。这也增加了对象描述的鲁棒性,因为在有遮挡或复杂背景的影响时,越靠近对象外围的点越不靠。
//t_w和t_h分别为检测窗口的宽度和高度
h = pow(((double)t_w)/2,2) + pow(((double)t_h)/2,2); //带宽
//初始化权值矩阵和目标直方图
for (i = 0;i < t_w*t_h;i++)
{
m_wei[i] = 0.0;
}
for (i=0;i<4096;i++)
{
hist1[i] = 0.0;
}
//生成权值矩阵
for (i = 0;i < t_h; i++)
{
for (j = 0;j < t_w; j++)
{
dist = pow(i - (double)t_h/2,2) + pow(j - (double)t_w/2,2);
m_wei[i * t_w + j] = 1 - dist / h;
C += m_wei[i * t_w + j] ;
}
}
//计算目标权值直方
for (i = t_y;i < t_y + t_h; i++)
{
for (j = t_x;j < t_x + t_w; j++)
{
//rgb颜色空间量化为16*16*16 bins
q_r = ((u_char)current->imageData[i * current->widthStep + j * 3 + 2]) / 16;
q_g = ((u_char)current->imageData[i * current->widthStep + j * 3 + 1]) / 16;
q_b = ((u_char)current->imageData[i * current->widthStep + j * 3 + 0]) / 16;
q_temp = q_r * 256 + q_g * 16 + q_b;
hist1[q_temp] = hist1[q_temp] + m_wei[(i - t_y) * t_w + (j - t_x)] ;
}
}
//归一化直方图
for (i=0;i<4096;i++)
{
hist1[i] = hist1[i] / C;
}
颜色模型相似性度量
初始帧的目标模型
以一定间隔的颜色值为单位将取值为像素颜色值的特征空间分为多个特征值那么在初始帧包含目标的搜索窗口中第u 个特征值的概率为
式中x0是搜索窗口(n个像素)的中心像素坐标;xi是第i个像素的坐标;k( ||x||2 ) 是核函数,用来对颜色分布的概率密度进行加权,为什么要加权呢?
采用核函数估计法,在采样充分的情况下,能够渐进地收敛于任意的密度函数,即可以对服从任何分布的数据进行密度估计。
这样可以保证meanshift算法的收敛,才能用meanshift向量进行迭代。h表示核函数的带宽,一般等于窗口宽度的一半;函数b和δ 的作用是判断xi处的颜色值是否属于特征值u ,如果xi属于特征值u,
δ 的值取1,否则δ 的值取0;
C 是一个标准化的常量系数使得所有特征值的概率和为1。
权值的计算是通过核函数k调节的,也正是核函数k的引入,使得直方图匹配能和均值漂移算法结合起来。
当前帧的模型
计算当前帧(第N 帧)中搜索窗口的特征值u 的概率为
式中y0是当前帧搜索窗口的中心像素坐标,xi是第i个像素的坐标,Ch对应上式中的C。
相似性函数Bhattacharrya 距离
用巴氏系数度量目标直方图和候选直方图的相似性,巴氏系数越大,越相似。
相似性函数描述初始帧目标模型和当前帧模型的相似性度量定义为
所以为在领域中找到下一帧目标的位置,即是要在下一帧图像中找到一个候选窗口,使得候选直方图于目标直方图相似性最大,即最大化巴氏系数。
在领域内怎样搜索才能用最少的迭代次数使巴氏系数最大化呢?这就要用到meanshift向量。
meanshift向量
因为p中第一项与y无关,只需最大化第二项。而第二项恰好是用核函数加权的概率密度估计,这样,根据均值漂移理论,就可以用meanshift进行迭代找到概率密度的峰值,即第二项的最大值。
通过对相似性函数求最大值,即对y求偏导并令偏导数为0,可以推导出Mean shift向量
所以
其中g() 是加权函数k() 的导数
令y0 = y1, 用上式进行迭代计算, 直到||y1-y0||小于某一阈值或达到了最大迭代次数。Mean shift算法反复迭代最后得到在当前帧目标的最优位置y。
function [] = select()
close all;
clear all;
%%%%%%%%%%%%%%%%%%根据一幅目标全可见的图像圈定跟踪目标%%%%%%%%%%%%%%%%%%%%%%%
I=imread('result72.jpg');
figure(1);
imshow(I);
[temp,rect]=imcrop(I);
[a,b,c]=size(temp); %a:row,b:col
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%计算目标图像的权值矩阵%%%%%%%%%%%%%%%%%%%%%%%
y(1)=a/2;
y(2)=b/2;
tic_x=rect(1)+rect(3)/2;
tic_y=rect(2)+rect(4)/2;
m_wei=zeros(a,b);%权值矩阵
h=y(1)^2+y(2)^2 ;%带宽
for i=1:a
for j=1:b
dist=(i-y(1))^2+(j-y(2))^2;
m_wei(i,j)=1-dist/h; %epanechnikov profile
end
end
C=1/sum(sum(m_wei));%归一化系数
%计算目标权值直方图qu
%hist1=C*wei_hist(temp,m_wei,a,b);%target model
hist1=zeros(1,4096);
for i=1:a
for j=1:b
%rgb颜色空间量化为16*16*16 bins
q_r=fix(double(temp(i,j,1))/16); %fix为趋近0取整函数
q_g=fix(double(temp(i,j,2))/16);
q_b=fix(double(temp(i,j,3))/16);
q_temp=q_r*256+q_g*16+q_b; %设置每个像素点红色、绿色、蓝色分量所占比重
hist1(q_temp+1)= hist1(q_temp+1)+m_wei(i,j); %计算直方图统计中每个像素点占的权重
end
end
hist1=hist1*C;
rect(3)=ceil(rect(3));
rect(4)=ceil(rect(4));
%%%%%%%%%%%%%%%%%%%%%%%%%读取序列图像
myfile=dir('D:\matlab7\work\mean shift\image\*.jpg');
lengthfile=length(myfile);
for l=1:lengthfile
Im=imread(myfile(l).name);
num=0;
Y=[2,2];
%%%%%%%mean shift迭代
while((Y(1)^2+Y(2)^2>0.5)&num<20) %迭代条件
num=num+1;
temp1=imcrop(Im,rect);
%计算侯选区域直方图
%hist2=C*wei_hist(temp1,m_wei,a,b);%target candidates pu
hist2=zeros(1,4096);
for i=1:a
for j=1:b
q_r=fix(double(temp1(i,j,1))/16);
q_g=fix(double(temp1(i,j,2))/16);
q_b=fix(double(temp1(i,j,3))/16);
q_temp1(i,j)=q_r*256+q_g*16+q_b;
hist2(q_temp1(i,j)+1)= hist2(q_temp1(i,j)+1)+m_wei(i,j);
end
end
hist2=hist2*C;
figure(2);
subplot(1,2,1);
plot(hist2);
hold on;
w=zeros(1,4096);
for i=1:4096
if(hist2(i)~=0) %不等于
w(i)=sqrt(hist1(i)/hist2(i));
else
w(i)=0;
end
end
%变量初始化
sum_w=0;
xw=[0,0];
for i=1:a;
for j=1:b
sum_w=sum_w+w(uint32(q_temp1(i,j))+1);
xw=xw+w(uint32(q_temp1(i,j))+1)*[i-y(1)-0.5,j-y(2)-0.5];
end
end
Y=xw/sum_w;
%中心点位置更新
rect(1)=rect(1)+Y(2);
rect(2)=rect(2)+Y(1);
end
%%%跟踪轨迹矩阵%%%
tic_x=[tic_x;rect(1)+rect(3)/2];
tic_y=[tic_y;rect(2)+rect(4)/2];
v1=rect(1);
v2=rect(2);
v3=rect(3);
v4=rect(4);
%%%显示跟踪结果%%%
subplot(1,2,2);
imshow(uint8(Im));
title('目标跟踪结果及其运动轨迹');
hold on;
plot([v1,v1+v3],[v2,v2],[v1,v1],[v2,v2+v4],[v1,v1+v3],[v2+v4,v2+v4],[v1+v3,v1+v3],[v2,v2+v4],'LineWidth',2,'Color','r');
plot(tic_x,tic_y,'LineWidth',2,'Color','b');
end
下图是我在一张图上面实现的迭代shift,首先选中一块目标区域,计算好目标直方图,然后将候选区域从目标区域的位置平移一段距离,执行meanshift算法,结果候选区域慢慢收敛到了目标区域,图上绿十字代表整个shift的轨迹。这就是跟踪的基础了,把在同一张图上执行meanshift改为在连续两帧图像上执行就可以实现跟踪了。