tarjan算法之 割边，割点

先介绍几个概念：

1.割边：在连通图中，删除了连通图的某条边后，图不再连通。，这样的边叫做割边，也称作桥。

2.割点：在连通图中，删除了连通图的某个点以及与这个点相连的边后，图不再连通。这样的点叫做割点。

3.dfs搜索树：用 dfs 遍历图时，按照遍历次序的不同，我们可以得到一颗 dfs 搜索树。

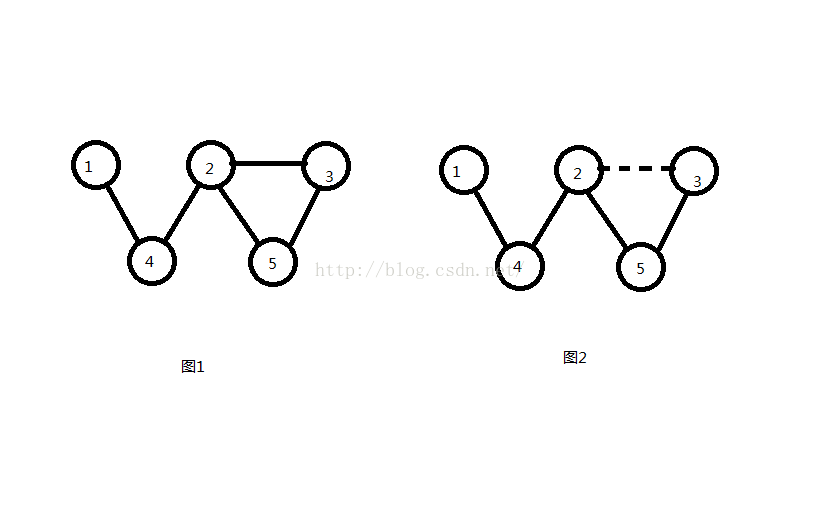
举个例子，对这个图一来说，其dfs搜索树便是图二

图中还有几个概念

树边：在搜索树中实线所示，表示dfs过程中访问 未访问结点 时所经过的边，也叫父子边

回边：在搜索树中虚线所示，表示dfs过程中遇到 已访问结点 时所经过的边，也叫返祖边、后向边。

割点包含两类结点：

1.对于根节点u，如果u有不止一棵子树（两棵及两棵以上），则该跟节点u为割点

2.对于非叶子且非根结点（叶子结点一定不是割点），若其中的某棵子树的结点均没有指向u的祖先结点的回边，说明删除u之后，根节点与该棵子树的结点不再连通，则结点 u 为割点。

我们用dfn[u]数组来记录u结点的dfs次序，low[u]来记录结点 u 或 u 的子树通过非父子边（这里的子指的是u，父指的是u的父亲结点）追溯到最早的祖先结点（dfs次序最小的结点），那么low[u]可以这么得到

若(u,v)是树边，则low[u]=min(low[u],low[v]);

若(u,v)是回边且v不是u的父亲，则low[u]=min(low[u],dfs[v]);

对于图一，dfn和low数组分别为

index	0	1	2	3	4	5	6
dfn		1	3	5	2	4
low		1	3	3	2	3

对于割点的第一种情况，很容易判断子树的个数，用child变量记录一下就好了

对于割点的第二种情况，当（u，v）为树边且low[v]>=dfn[u]时，结点u才是割点。

而对于割边，当（u，v）为树边且dfs[u]>low[v]时，表示v结点智能通过该边（u，v）与u连通，那么（u，v）即为割边。

#pragma warning(disable:4996)
#include <cstdio>
#include <vector>
#include <cstring>
#include <set>
#include <algorithm>
#define make_pair pair<int,int>
#define N 20010
using namespace std;

vector<int>to[N];
vector<pair<int, int>>line;//存割边
set<int>ans;//存割点
int father[N];   // 0 表示根节点，-1 表示未遍历， 否则代表父亲结点
//dfn[u]数组表示结点 u 的dfs遍历次序，low[u]数组表示 u 及其子树能到达的最远祖宗结点
int dfn[N], low[N], dfs_clock = 0;

void init(){
	dfs_clock = 0;
	memset(father, -1, sizeof father);
	father[1] = 0;
}

void dfs(int u){
	dfn[u] = low[u] = ++dfs_clock;
	int child = 0;

	for (int i = 0; i < to[u].size(); i++){
		int v = to[u][i];
		//未访问过 v 点
		if (father[v] == -1){
			child++;
			father[v] = u;
			dfs(v);
			low[u] = min(low[u], low[v]);

			//结点 u 是根节点，且有不止一个子树
			if (father[u] == 0 && child>1)
				ans.insert(u);

			//结点 u 不是根节点，
			if (father[u] != 0 && dfn[u] <= low[v])
				ans.insert(u);

			//割边的情况
			if (low[v] > dfn[u])line.push_back(make_pair(min(u, v), max(u, v)));
		}
		else if (father[u] != v){
			low[u] = min(low[u], dfn[v]);
		}
	}

}