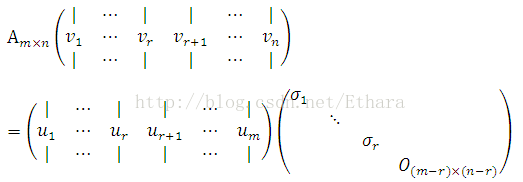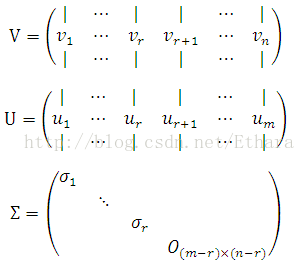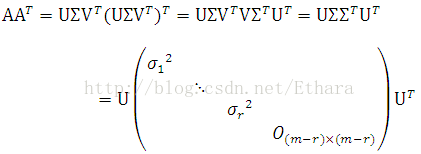Meditation on Singular Value Decomposition

Meditation on Singular Value Decomposition
Ethara

Singular Value Decomposition (SVD) is considered as the final and best factorization of a matrix, as described by Professor Gilbert Strang from Massachusetts Institute of Technology. Here is what SVD says,

Any matrix A whatsoever can be decomposed into

where SIGMA is a diagonal matrix, U and V are two orthogonal matrices.

Question is, how could it become possible? After thorough meditation, I will give a natural motivation to this perfect decomposition of a matrix in this paper.

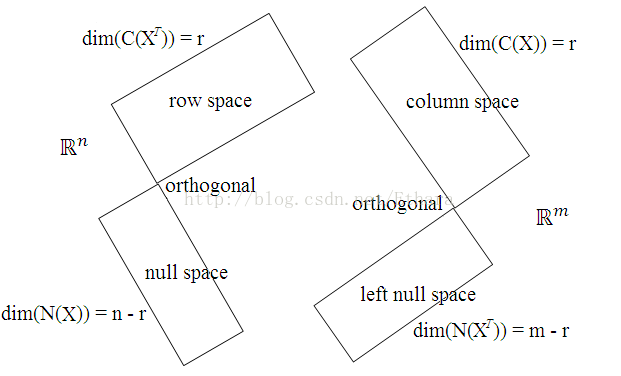
Figure 1. Four fundamental subspaces of matrix X

Proof on SVD

Suppose we are given an m-by-n matrix X whose rank is r. Since any matrix can be viewed as comprised of four fundamental subspaces, we can depict Figure 1 for matrix X.

Through Gram-Schmidt orthogonalization, we can always obtain all of the orthonormal bases in each subspace of X, which are,

v₁, …,v_r are orthonormal bases in the row space of X,

v_r+1, …,v_n are orthonormal bases in the null space of X,

u₁, …,u_r are orthonormal bases in the column space of X,

u_r+1, …,u_m are orthonormal bases in the left null space of X.

Here comes a challenging problem which will motivate SVD naturally. We are asked to find a linear transform given by an m-by-n matrix A that makes a subtle connection between the row space and the column space, i.e.,

where

Furthermore, taking the null space and the left null space of X into consideration, we can express this problem explicitly into the following equation.

Letting

yields

Since V is an orthogonal matrix, V is invertible and V^-1=V^T. We can obtain Equation (*),

Thus, if we can find appropriate matrices U, V and SIGMA, the proof on SVD is done. Now, let’s find them.

Using Equation (*), we have,

Noting that A^TA is a symmetric matrix, moreover, an n-order symmetric matrix S has n independent eigenvectors and can be decomposed as,

where the columns of Q are the eigenvectors of S and LAMBDA is a diagonal matrix with the eigenvalues of S, we can conclude that the columns of V are just the eigenvectors of A^TA and the entries on the primary diagonal in the diagonal matrix between V and V^T are just the eigenvalues of A^TA.

Likewise, we can find U in exactly the same way,

Therefore, similarly, the columns of U are just the eigenvectors of AA^T and the entries on the primary diagonal in the diagonal matrix between U and U^T are just the eigenvalues of AA^T.

Since V, U and SIGMA have been nailed down, now it’s time to declare our victory of proving the Singular Value Decomposition. Any matrix A whatsoever can be decomposed into

Postscript

Laymen are always looking upon a matrix as a simple box of numbers, while mathematicians like us are able to see what’s typically inside of this magical box, i.e., four fundamental subspaces of a matrix.