DOG算子及DOG尺度空间
DOG算子及DOG尺度空间
一.DOG算子
1.LOG算子
2.DOG算子
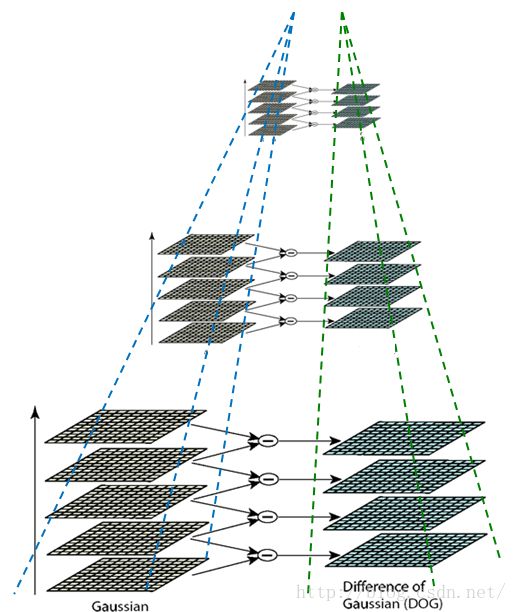
可以利用高斯差分来近似,其中差分是由两个高斯滤波与不同变量的卷积结果求得的,DOG是高斯函数的差分。它是可以通过将图像与高斯函数进行卷积得到一幅图像的低通滤波结果,即去噪过程,这里的Gaussian和高斯低通滤波器的高斯一样,是一个函数,即为正态分布函数。同时,它对高斯拉普拉斯LoG的近似,在某一尺度上的特征检测可以通过对两个相邻高斯尺度空间的图像相减,得到DoG的响应值图像。
基本理论:
也可以表示为:
DOG≜G(x,y,kσ)-G(x,y,σ),其中k的取值再好再1.5~1.6之间
用DOG卷积原图像I(x,y),得到一个尺度上的DOG图像
二.生成DOG尺度空间
1.生成高斯金字塔
高斯金字塔的组数:O=log2(min(m,n))-2([m,n]=size(原图像))
考虑一般图像的大小,先去金字塔的组数为4,每一组有4层。
在每个O(组)里,有4幅图像,每幅图像都是前一个图像通过高斯卷积获得,每次卷积的sigma不同,需要分别计算,但是对于不同组的同一层sigma是相同的。
计算sigma:
初始化值:第0层→sigma(0)=1.6,k=2^(1/3)
Sigma(1)=[(k^0*1.6*k)^2-(k^0*1.6)^2]^1/2;
Sigma(2)=[(k^1*1.6*k)^2-(k^1*1.6)^2]^1/2;
Sigma(3)=[(k^2*1.6*k)^2-(k^2*1.6)^2]^1/2;
……
一.DOG算子
1.LOG算子
高斯卷积函数定义为:
而原始图像与高斯卷积定义为:
可以通过先对高斯函数进行偏导操作,然后进行卷积求解。公式表示为:
和:
因此,我们可以把LOG核函数定义为:
2.DOG算子
可以利用高斯差分来近似,其中差分是由两个高斯滤波与不同变量的卷积结果求得的,DOG是高斯函数的差分。它是可以通过将图像与高斯函数进行卷积得到一幅图像的低通滤波结果,即去噪过程,这里的Gaussian和高斯低通滤波器的高斯一样,是一个函数,即为正态分布函数。同时,它对高斯拉普拉斯LoG的近似,在某一尺度上的特征检测可以通过对两个相邻高斯尺度空间的图像相减,得到DoG的响应值图像。
基本理论:
首先,高斯函数表示定义为:
其次,两幅图像的高斯滤波表示为:
最后,将上面滤波得到的两幅图像g1和g2相减得到:
即:可以DOG表示为:
也可以表示为:
DOG≜G(x,y,kσ)-G(x,y,σ),其中k的取值再好再1.5~1.6之间
用DOG卷积原图像I(x,y),得到一个尺度上的DOG图像
二.生成DOG尺度空间
1.生成高斯金字塔
高斯金字塔的组数:O=log2(min(m,n))-2([m,n]=size(原图像))
考虑一般图像的大小,先去金字塔的组数为4,每一组有4层。
在每个O(组)里,有4幅图像,每幅图像都是前一个图像通过高斯卷积获得,每次卷积的sigma不同,需要分别计算,但是对于不同组的同一层sigma是相同的。
计算sigma:
初始化值:第0层→sigma(0)=1.6,k=2^(1/3)
Sigma(1)=[(k^0*1.6*k)^2-(k^0*1.6)^2]^1/2;
Sigma(2)=[(k^1*1.6*k)^2-(k^1*1.6)^2]^1/2;
Sigma(3)=[(k^2*1.6*k)^2-(k^2*1.6)^2]^1/2;
……
对第L组的图像进行和DOG进行卷积后,对第L组的最后一层图像进行间隔一个像素的降采样(1:2:end),得到第L+1组的第一层图像,然后以这个图像为L+1组图像的第0层循环和DOG进行卷积,直到满足某个终止条件为止,返回所有的DOG图像形成DOG尺度空间