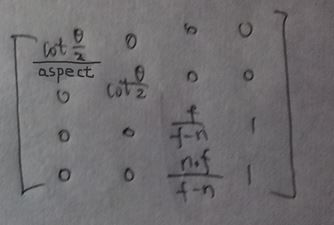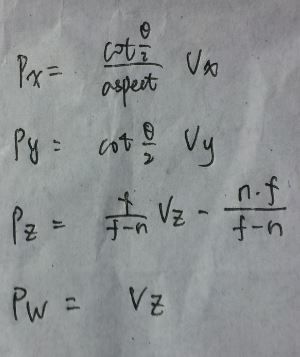龙书中拾取例子解析

前几天看到龙书拾取的例子,以为点击了屏幕上一点,则这点转到视图空间就是

(这里的P为投影矩阵)

百思不得其解.

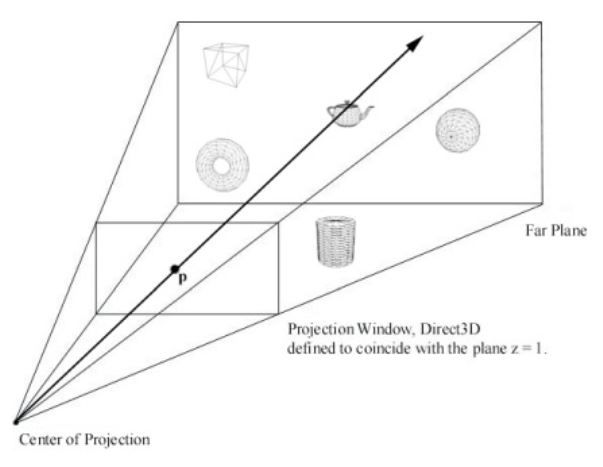
结果是我理解错误,也许是龙书误导了,它说投影平面在z=1处,

但是我认为投影平面跟GL一样,还是在近平面,不然推出来的各种投影矩阵公式中就没有n了,也许我们说的投影平面根本就不是同一个意思- -!!!

所以澄清下,点击了屏幕上一点,转到视图空间中,这点位于(0,0,0)到(Vx,Vy,Vz)的射线所在的直线上,所以这点不一定是(Vx,Vy,Vz)

好吧,下面来详细整个拾取过程,

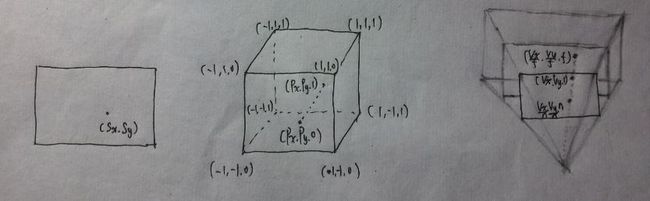
首先,我们知道在窗口个点击一点后,它的坐标是二维的(Sx,Sy),那么这个二维坐标在标准设备坐标空间中就确定了一条从(Px,Py,0)到(Px,Py,1)的一条线段(其实更准确表述应该是确定了从(PxPw,PyPw,0,Pw)到(PxPw,PyPw,Pw,Pw)这条线段,因为Pw并不一定等于1),这条线段转到视图空间中就变成了一条从(Vx/n,Vy/n,n)到(Vx/f,Vx/f,f)的一条线段,点(Vx,Vy,1)位于这条线段所在的直线上

下面给出整个推导过程

先看(Sx,Sy)转(Px,Py)的过程

视口变换矩阵为

所以

注意这里已经假设Pw=1了

这样在标准设备坐标空间中就确定了一条从(Px,Py,0)到(Px,Py,1)的一条线段.

再看D3DXMatrixPerspectiveFovLH这个函数推导出的视图变换矩阵

则(Vx,Vy,Vz,1)到(Px,Py,Pz,Pw)的转换为

由于前面的推导公式 已经假设Pw=1了所以这里Vz=1.但是龙书由此就说Vz=1为投影平面,实在令人蛋疼啊!~~~

则可以得到

Vx=Px / P_00

Vy=Py / P_11

Vz=1

其中

P_00=cot(θ/2)/aspect

P_11=cot(θ/2)

再将

代入上式

则可得

最后看下龙书里的一段代码

d3d::Ray CalcPickingRay(int x,int y)
{
	float px = 0.0f;
	float py = 0.0f;
	D3DVIEWPORT9 vp;
	Device->GetViewport(&vp);
	D3DXMATRIX proj;
	Device->GetTransform(D3DTS_PROJECTION,&proj);
	px=(((2.0f*x)/vp.Width)-1.0f)/proj(0,0);
	py=(((-2.0f*y)/vp.Height)+1.0f)/proj(1,1);
	d3d::Ray ray;
	ray._origin = D3DXVECTOR3(0.0f,0.0f,0.0f);
	ray._direction=D3DXVECTOR3(px,py,1.0f);
	return ray;
}