双线性插值的图像缩放算法的研究与实现
引用:http://www.cnblogs.com/okaimee/archive/2010/08/18/1802580.html
一、引言
数字图像处理的对象因其涉及到社会的各个领域,倍受到越来越多的关注,而图像缩放作为数字图像处理中的基本操作尤为重要,在社会的很多领域都需要对图像进行放大和缩小。利用VC++的MFC类库中的StretchBlt函数可以很容易的实现图像放大和缩小,但是当放大或缩小的比率比较大时就容易出现失真现象,因此必须进行改进。本文提出了一种双线性插值算法,用以改进图像的缩放质量。
二、空间变换
图像的空间变换,也称几何变换或几何运算,包括图像的平移、旋转、镜像变换、转置、缩放等。几何运算可改变图像中各物体之间的空间关系,这种运算可以被看成是将各物体在图像内移动。
空间变换可如下表示:设(u,v)为源图像上的点,(x,y)为目标图像上的点,则空间变换就是将源图像上(u,v)处的颜色值与目标图像上(x,y)处的颜色对应起来。
(u,v) ß----------------à (x,y)
并具有以下关系:
x=X(u,v),y=Y(u,v) (即由(u,v)计算对应点(x,y) ) (1.1)
或
u=U(x,y),v=V(x,y) (即由(x,y)反求对应点(u,v) )(1.2)其中X(u,v)、Y(u,v)、U(x,y)、V(x,y)均为变换。由(1.1)对应的变换称作向前映射法也叫像素移交法,而由(1.2)对应的变换称作向后映射法也叫像素填充法,向后映射法是向前映射法的逆。
对于向前映射法来说,由于许多输入像素可能映射到输出图像的边界之外,所以,向前映射法有些浪费,而且每个输出像素的灰度值可能要由许多输入像素的灰度值来决定,因此要涉及多次运算。如果空间变换中包括缩小处理,则会有四个以上的输入像素来决定输出像素的灰度值;如果含有放大处理,则一些输出像素可能被漏掉。而向后映射算法是逐像素、逐行地产生输出图像。每个像素的灰度级由最多四个像素参与的插值所惟一确定,虽然向后映射法比向前映射法要复杂,但是向后映射法对于一般的应用却具有更为现实的意义。本文就是采取了向后映射法来实现图像缩放的。
三.双线性插值
最简单的插值算法是最邻近插值,也称为零阶插值。它输出的像素灰度值就等于距离它映射到的位置最近的输入像素的灰度值,最邻近插值算法简单,在许多情况下都能得到令人满意的结果,但是当图像中包含像素之间灰度级有变化的细微结构时,最邻近算法会在图像中产生人为加工的痕迹。双线性插值算法计算量比零阶插值大,但缩放后图像质量高,不会出现像素值不连续的情况,这样就可以获得一个令人满意的结果。
双线性插值是利用了需要处理的原始图像像素点周围的四个像素点的相关性,通过双线性算法计算得出的。对于一个目的坐标,通过向后映射法得到其在原始图像的对应的浮点坐标(i+u,j+v),其中i,j均为非负整数,u,v为[0,1]区间的浮点数,则这个像素的值 f(i+u,j+v) 可由原图像中坐标为 (i,j)、(i+1,j)、(i,j+1)、(i+1,j+1)所对应的周围四个像素的值决定,即:f(i+u,j+v) =(1-u)×(1-v) ×f(i,j)+(1-u) ×v×f(i,j+1)+u×(1-v) ×f(i+1,j)+u×v×f(i+1,j+1),其中f(i,j)表示源图像(i,j)处的像素值,以此类推,这就是双线性内插值法。
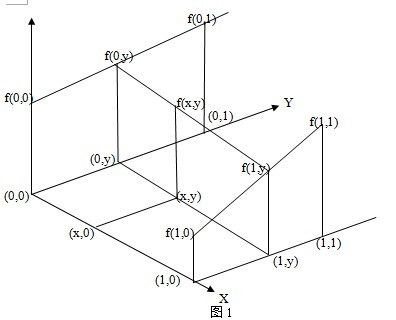
如图1所示,已知(0,0)、(0,1)、(1,0)、(1,1)四点的灰度,可以由相邻像素的灰度值f(0,0)和f(1,0) 在X方向上线性插值求出(x,0)的灰度f(x,0),由另外两个相邻像素f(0,1)和f(1,1)在X方向上线性插值可求出(x,1)的灰度f(x,1),最后由f(x,0)、f(x,1)在Y方向上进行线性插值就可以得到(x,y)的灰度f(x,y)。
四.算法
1.算法
假设原始图像大小为size=m×n,其中m与n分别是原始图像的行数与列<数。若图像的缩放因子是t(t>0),则目标图像的大小size=t×m×t×n。对于目标图像的某个像素点P(x,y)通过P*1/t可得到对应的原始图像坐标P’( x1,y1),其中x1=x/t,y1=y/t,由于x1,y1都不是整数所以并不存在这样的点,这样可以找出与它相邻的四个点的灰度f1、f2、f3、f4,使用双线性插值算法就可以得到这个像素点P’(x1,y1)的灰度,也就是像素点P(x,y)的灰度。
一个完整的双线性插值算法可描述如下:
(1) 通过原始图像和比例因子得到新图像的大小,并创建新图像。
(2) 由新图像的某个像素(x,y)映射到原始图像(x’,y’)处。
(3) 对x’,y’取整得到(xx,yy)并得到(xx,yy)、(xx+1,yy)、(xx,yy+1)和(xx+1,yy+1)的值。
(4) 利用双线性插值得到像素点(x,y)的值并写回新图像。
(5) 重复步骤(2)直到新图像的所有像素写完。
2.核心代码
- //函数名Bilinear
- //参数float k
- //返回值无
- //作用利用双线性插值来实现图像缩放
- void CChildView::Bilinear(float k)
- {
- int nBpp=m_imPicture .GetBPP ();
- int widthNew,heightNew;//新图像的宽度和高度
- float widthScale=(float)(1.0/k),heightScale=(float)(1.0/k);
- float xx,yy;
- int a,b;
- int rr,gg,bb;//保存R、G、B分量
- //得到新图像的宽度和高度
- widthNew=(int)(m_imPicture .GetWidth ()*k);
- heightNew =(int)(m_imPicture .GetHeight ()*k);
- //利用新图像的宽度和高度来创建新图像
- m_imNewPicture .Destroy ();
- m_imNewPicture .Create (widthNew ,heightNew ,nBpp);
- //得到新、老图像的每行的字节数
- int nPitch=m_imPicture .GetPitch ();
- int nPitchNew=m_imNewPicture .GetPitch ();
- //得到新、老图像的数据指针
- LPBYTE pBitsNew=(LPBYTE)m_imNewPicture .GetBits ();
- LPBYTE pBits=(LPBYTE)m_imPicture .GetBits ();
- if(m_imPicture.GetBPP ()!=24){
- MessageBox ("必须是24位图像或8位图像");
- m_imNewPicture .Destroy ();
- Invalidate();
- return ;
- }
- for(int x=(int)k;x<widthNew -k;x++){
- for(int y=(int)k;y<heightNew -k;y++){
- xx=x*widthScale ;
- yy=y*heightScale ;
- if(xx<=1e-8){
- xx=0;
- }
- if(xx>m_imPicture .GetWidth ()-2)
- xx=(float)(m_imPicture .GetWidth ()-2);
- if(yy<=1e-8)
- yy=0;
- if(yy>m_imPicture .GetHeight ()-2)
- yy=(float)(m_imPicture .GetHeight ()-2);
- a=(int)xx;
- b=(int)yy;
- //分别得到对应像素的R、G、B值并用双线性插值得到新像素的R、G、B值
- int r11,r12,r21,r22;
- r11=*(pBits+b*nPitch+3*a+2);
- r12=*(pBits+b*nPitch+3*(a+1)+2);
- r21=*(pBits+(b+1)*nPitch+3*a+2);
- r22=*(pBits+(b+1)*nPitch+3*(a+1)+2);
- rr=(int)(r11*(a+1-xx)*(b+1-yy)+r12*(a+1-xx)*(yy-b)
- +r21*(xx-a)*(b+1-yy)+r22*(xx-a)*(yy-b));
- int g11,g12,g21,g22;
- g11=*(pBits+b*nPitch+3*a+1);
- g12=*(pBits+b*nPitch+3*(a+1)+1);
- g21=*(pBits+(b+1)*nPitch+3*a+1);
- g22=*(pBits+(b+1)*nPitch+3*(a+1)+1);
- gg=(int)(g11*(a+1-xx)*(b+1-yy)+g12*(a+1-xx)*(yy-b)
- +g21*(xx-a)*(b+1-yy)+g22*(xx-a)*(yy-b));
- int b11,b12,b21,b22;
- b11=*(pBits+b*nPitch+3*a);
- b12=*(pBits+b*nPitch+3*(a+1));
- b21=*(pBits+(b+1)*nPitch+3*a);
- b22=*(pBits+(b+1)*nPitch+3*(a+1));
- bb=(int)(b11*(a+1-xx)*(b+1-yy)+b12*(a+1-xx)*(yy-b)
- +b21*(xx-a)*(b+1-yy)+b22*(xx-a)*(yy-b));
- //将得到的新R、G、B值写到新图像中
- *(pBitsNew +y*nPitchNew +x*3)=min(255,bb);
- *(pBitsNew +y*nPitchNew +x*3+1)=min(255,gg);
- *(pBitsNew +y*nPitchNew +x*3+2)=min(255,rr);
- }
- }
- m_imPicture .Destroy ();
- Invalidate ();
- }
五.结语
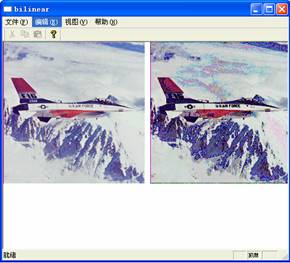
本文介绍了一种利用双线性插值来实现图像缩放的算法,通过图2可以看到这种算法和传统的利用StretchBlt来实现图像缩放相比具有很大的改善。StretchBlt实现的图像具有很大的失真,并且随着缩小的比率越大失真也越严重;而双线性插值算法则很好地解决了这个问题,可以得到很高的清晰度,这种方法可以广泛应用在图像变形、计算机动画、计算机辅助设计等领域。所附源代码在VC++.NET 2003下编译通过。
图2
注:左图是利用本文介绍的双线性插值算法缩小一倍得到图像,右图是利用StretchBlt缩小一倍得到图像。