状压DP
最近做了几道状压DP的题,在此汇总
状压DP就是使用二进制压缩状态进行动态规划
T1最佳挑水
Description
小Y喜欢挑水,小Y的家里有n(n是偶数)只桶,设小Y挑得是i,j两只桶,则挑水一趟需要走time[i,j]分钟。小Y想要在最少的时间内用自己的力量把家里所有的空桶装满。
小Y觉得这是个难题,于是来找你帮忙编写一个程序来找出一种最佳挑水方案。
Input
输入文件中的的第一行为一个整数n(4<=n<=18)。
接下来的n行,每行有n个数,表示了time矩阵。其中:time矩阵中每一个数都是小于等于32768正整数,且time[i,i]是没有用的。
注意:time[i,j]=time[j,i]。
Output
输出文件中仅一行为一个数,即最佳挑水方案的最少时间。
Sample Input
4
0 100 5 100
100 0 100 11
5 100 0 100
100 11 100 0
Sample Output
16
分析:
观察题目限制,可以发现,n的值非常小,自然想到状压DP。
状态s表示当前哪些水桶已经装了水为1,其余为0。枚举接下来挑i,j两桶水,那么f[s+2^(i-1)+2^(j-1)]]=f[s]+time[i,j];答案就是f[2^n-1]。
code:
>var
n,i,j,k,x,y:longint;
f:array[0..262144] of longint;
d:array[1..10000000] of longint;
a:array[1..20,1..20] of longint;
g:array[0..19] of longint;
function min(a,b:longint):longint;
begin if a<b then exit(a) else exit(b);end;
begin
read(n);g[1]:=1;for i:=2 to n+1 do g[i]:=g[i-1]*2;
for i:=1 to n do
begin
for j:=1 to n do read(a[i,j]);
end;
fillchar(f,sizeof(f),127);
f[0]:=0;x:=0;y:=1;d[1]:=0;
while x<y do
begin
inc(x);i:=d[x];
for j:=1 to n-1 do
if (i and g[j])=0 then
begin
for k:=j+1 to n do
if ((i and g[k])=0) then
begin
if f[i]+a[j,k]<f[i+g[j]+g[k]] then
begin
f[i+g[j]+g[k]]:=f[i]+a[j,k];
inc(y);d[y]:=i+g[j]+g[k];
end;
end;
end;
end;
writeln(f[g[n+1]-1]);
end.第一道只是一道水题,用来热热身而已。
T2Fix
Description
有N个 点(N<= 18)。其中一些是固定的,一些是不固定的。从两个固定的点连边到一个不固定的点就可以使这个不固定的点固定。给出每个点的坐标,问最短用多长的边可以使所有点固定。
Input
多组数据,每组数据的第一行是N,第2-n+1行有三个整数x,y,z,(x,y)为第i个点的坐标,z=1表示这个点固定,z=0表示这个点不固定。输入N=0代表数据结束。
Output
每组数据输出一行一个整数,代表固定所有点最少的边的长度(保留6位小数)。若无法固定所有的点,输出“No Solution”
Sample Input
4
0 0 1
1 0 1
0 1 0
1 1 0
3
0 0 1
1 1 0
2 2 0
0
Sample Output
4.414214
No Solution
分析:
观察题目限制,可以发现,n的值非常小,自然想到状压DP。
状态s表示当前已固定的点,1为固定,0为不固定。转移方程可以轻易得到。
不过,只是像第一题那样做的话,会发现时间复杂度为O(2^n*n^3)。明显会超时,这是可以想到一个小优化。如果想使总边长最小的话,每个点都连到最近两个点显然是最优的。但是连边必须连已经固定的,所以就把每个点连到任意其余两个点的最小边长排序。在转移时直接选用合法的边最短的,时间复杂度就很低了。
code:
var
n,i,j,k,x,y,s,l,q,w:longint;
f:array[1..262144] of double;
g:array[1..19] of longint;
d:array[1..1000000] of longint;
a:array[1..18,1..18] of double;
c:array[1..18,0..1000,1..2]of longint;
c1:array[1..18,0..1000] of double;
b:array[1..18,1..3] of longint;
function jl(i,j:longint):double;
begin
exit(sqrt(sqr(b[i,1]-b[j,1])+sqr(b[i,2]-b[j,2])));
end;
procedure px(x,y:longint);
var
l,r:longint;
t1,m:double;
t:array[1..2] of longint;
begin
l:=x;r:=y;m:=c1[i,(x+y)div 2];
repeat
while c1[i,x]<m do inc(x);
while c1[i,y]>m do dec(y);
if x<=y then
begin
t1:=c1[i,x];c1[i,x]:=c1[i,y];c1[i,y]:=t1;
t:=c[i,x];c[i,x]:=c[i,y];c[i,y]:=t;
inc(x);dec(y);
end;
until x>y;
if l<y then px(l,y);
if x<r then px(x,r);
end;
begin
g[1]:=1;for i:=2 to 19 do g[i]:=g[i-1]*2;
read(n);
while n<>0 do
begin
s:=0;
for i:=1 to n do
begin
read(b[i,1],b[i,2],x);
if x=1 then s:=s+g[i];
for j:=1 to i-1 do begin a[i,j]:=jl(i,j);a[j,i]:=a[i,j];end;
end;
for i:=1 to n do
begin
c[i,0,1]:=0;
for j:=1 to n-1 do
if (i<>j) then
begin
for k:=j+1 to n do
if (i<>k)and(j<>k) then
begin
inc(c[i,0,1]);
c[i,c[i,0,1],1]:=j;
c[i,c[i,0,1],2]:=k;
c1[i,c[i,0,1]]:=a[i,j]+a[i,k];
end;
end;
px(1,c[i,0,1]);
end;
for i:=1 to g[n+1] do f[i]:=maxlongint*10000;
f[s]:=0;x:=0;y:=1;d[1]:=s;
while x<y do
begin
inc(x);i:=d[x];
for j:=1 to n do
if (i and g[j])=0 then
begin
for k:=1 to c[j,0,1] do
begin
q:=c[j,k,1];w:=c[j,k,2];
if ((i and g[q])<>0)and((i and g[w])<>0) then
begin
if (f[i]+c1[j,k]<f[i+g[j]]) then
begin
f[i+g[j]]:=f[i]+c1[j,k];
inc(y);d[y]:=i+g[j];
end;
break;
end;
end;
end;
end;
if f[g[n+1]-1]=maxlongint*10000 then writeln('No Solution') else writeln(f[g[n+1]-1]:0:6);
read(n);
end;
end.玩诈欺的小杉
Description
在小杉的面前有一个N行M列的棋盘,棋盘上有N*M个有黑白棋的棋子(一面为黑,一面为白),一开始都是白面朝上。
小杉可以对任意一个格子进行至多一次的操作(最多进行N*M个操作),该操作使得与该格同列的上下各2个格子以及与该格同行的左右各1个格子以及该格子本身翻面。
例如,对于一个5*5的棋盘,仅对第三行第三列的格子进行该操作,得到如下棋盘(0表示白面向上,1表示黑面向上)。
00100
00100
01110
00100
00100
对一个棋盘进行适当的操作,使得初始棋盘(都是白面朝上)变成已给出的目标棋盘的操作集合称作一个解法。
小杉的任务是对给出的目标棋盘求出所有解法的总数。
Input
第一行有3个正整数,分别是N和M和T(1<=N,M<=20,1<=T<=5)
接下来T个目标棋盘,每个目标棋盘N行,每行M个整数之前没有空格且非0即1,表示目标棋盘(0表示白面朝上,1表示黑面朝上)
两个目标棋盘之间有一个空行。
特别地,对于30%的数据,有1<=N,M<=15
Output
输出T行,每行一个整数,表示能使初始棋盘达到目标棋盘的解法总数
Sample Input
4 4 2
0010
0010
0111
0010
0010
0110
0111
0010
Sample Output
1
1
分析:
观察题目限制,可以发现,m的值非常小,自然想到状压DP。(好像每题第一句话都是这个)
从左往右做。如果当前这个点的左边是1,那么就必须在这里操作一下。同时更改这一列和下一列的状态(在一列的某一点操作,这一列和下一列的状态都会受影响)。
那么怎么操作呢? 可以借助异或来完成 1 xor 1=0 0 xor 1=1。这和这里的操作完全一样。
想到先第0列的状态,而第0列为1的行在第1列的这些行必须操作。看似问题已经解决了:枚举第0列的状态,一列一列往右推。如果最后一列的状态为0,这个方案就是可行的。仔细想一下会发现,如果每一列都枚举在哪一行必须操作,会超时。
用位运算可以完美的解决超时问题。将第0列的状态直接异或第一列的状态,就可以的到第一列操作后的状态(暂时只考虑一列)。如:
00
00
10
11
01
操作后变为
00
00
11
10
01
但是这样操作只有同一行会变化,操作后,这一列的上两行和下两行都要变化。还拿第0列和第一列举例,将第0列的状态*2,相当于整体下移一行。将状态 *4相当于整体下移两行。/2就是上移。那么像下面,第0列分别上下移后再异或
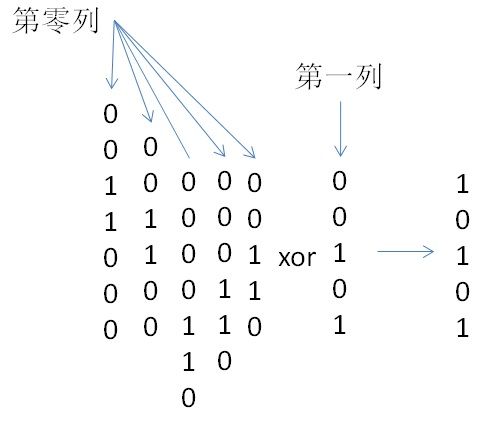
这样不仅程序优美,而且时间复杂度低了不少。
code:
var
i,j,k,n,m,ans,t,x,y,z:longint;
s:string;
a:array[0..20] of longint;
b:array[1..20] of string;
begin
readln(n,m,t);
while t>0 do
begin
dec(t);ans:=0;
fillchar(a,sizeof(a),0);
for i:=1 to n do readln(b[i]);
for j:=1 to m do
begin
a[j]:=0;
for i:=1 to n do
begin
if b[i][j]='1' then a[j]:=a[j]+(1<<(i-1));
end;
end;
for i:=0 to 1<<n-1 do
begin
x:=i;y:=a[1];
for j:=1 to m do
begin
z:=a[j+1] xor x;
x:=(x xor y xor(x<<1)xor(x<<2)xor(x>>1)xor(x>>2))and((1<<n)-1);
y:=z;
end;
if x=0 then inc(ans);
end;
writeln(ans);
readln;
end;
end.T1【NOI2001】炮兵阵地
Description
司令部的将军们打算在N*M的网格地图上部署他们的炮兵部队。一个N*M的地图由N行M列组成,地图的每一格可能是山地(用“H” 表示),也可能是平原(用“P”表示),如下图。在每一格平原地形上最多可以布置一支炮兵部队(山地上不能够部署炮兵部队);一支炮兵部队在地图上的攻击范围如图中黑色区域所示:如果在地图中的灰色所标识的平原上部署一支炮兵部队,则图中的黑色的网格表示它能够攻击到的区域:沿横向左右各两格,沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。 现在,将军们规划如何部署炮兵部队,在防止误伤的前提下(保证任何两支炮兵部队之间不能互相攻击,即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内),在整个地图区域内最多能够摆放多少我军的炮兵部队。
Input
文件的第一行包含两个由空格分割开的正整数,分别表示N和M; 接下来的N行,每一行含有连续的M个字符(‘P’或者‘H’),中间没有空格。按顺序表示地图中每一行的数据。 N≤100;M≤10。
Output
文件仅在第一行包含一个整数K,表示最多能摆放的炮兵部队的数量
Sample Input
5 4
PHPP
PPHH
PPPP
PHPP
PHHP
Sample Output
6
分析:
观察题目限制,可以发现,m的值非常小,自然想到状压DP。(好像每题第一句话都是这个)
f[i,j,k]表示当前做到第i行,上一次状态为j,这一次状态为k可以放的炮兵数量。(i滚动)
只需要判断是否合法就行了。判断合法需要判断同一行的任意两个炮兵在两格外,枚举的三行炮兵互相不在同一列且炮兵都在平原上。要注意细节。
code:
var
n,m,i,j,k,l,x,y,ans,q:longint;
s:array[0..200] of string;
f:array[0..1,0..1024,0..1024] of longint;
a:array[0..200] of longint;
c,b:array[-10..200] of longint;
bz:boolean;
function max(a,b:longint):longint;begin if a>b then exit(a)else exit(b);end;
function pd(a:longint):boolean;
var
i,x:longint;
begin
x:=-5;
for i:=1 to m do
if (a and (1<<(i-1)))<>0 then
begin
if i-x <=2 then exit(false);
x:=i;
end;
exit(true);
end;
begin
readln(n,m);
for i:=1 to n do
begin
readln(s[i]);
x:=0;
for j:=1 to m do if s[i][j]='H' then x:=x+1<<(j-1);
a[i]:=x;
end;
for k:=1 to 1<<m-1 do
if (k and a[1]=0)and(pd(k)) then
begin
x:=0;
for j:=1 to m do if (k and (1<<(j-1)))<>0 then inc(x);
f[1,0,k]:=x;
end;
for i:=2 to n do
begin
fillchar(f[i mod 2],sizeof(f[i mod 2]),0);
for k:=0 to (1<<m)-1 do
if (k and a[i-2]=0)and(pd(k)) then
begin
for j:=0 to (1<<m)-1 do
if (k and j=0)and(j and a[i-1]=0)and(pd(j)) then
begin
for l:=0 to (1<<m)-1 do
if ((k or j)and l=0)and(l and a[i]=0)and(pd(l)) then
begin
x:=0;
for q:=1 to m do if l and (1<<(q-1))<>0 then inc(x);
f[i mod 2,j,l]:=max(f[i mod 2,j,l],f[(i+1)mod 2,k,j]+x);
end;
end;
end;
end;
ans:=0;
for i:=0 to 1<<m-1 do
begin
for j:=0 to 1<<m-1 do
begin
ans:=max(ans,f[n mod 2,i,j]);
end;
end;
writeln(ans);
end.以上就是这几天做过的状压DP题。以前对状压DP一直不熟练,这几题做过之后,感觉熟练不少。这几题也是非常经典的题,在这里推荐给大家。