凸包问题的五种解法
前言:
首先,什么是凸包?
说凸包首先要说凸性的定义,简单点说就是平面邻域中任意两点所在的线段上的点都在该邻域中,则该邻域具有凸性。简单推敲一下,就可以发现如果邻域中存在一阶导数不连续的点一定无法被某点集线性表示出来。再往下的内容属于数学分析了,对我们的算法设计帮助不大,暂时先不管。
假设平面上有p0~p12共13个点,过某些点作一个多边形,使这个多边形能把所有点都“包”起来。当这个多边形是凸多边形的时候,我们就叫它“凸包”。如下图:
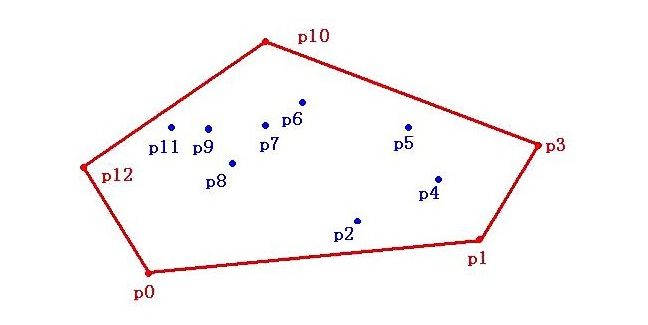
然后,什么是凸包问题?
我们把这些点放在二维坐标系里面,那么每个点都能用 (x,y) 来表示。
现给出点的数目13,和各个点的坐标。求构成凸包的点?
解一:穷举法(蛮力法)
时间复杂度:O(n³)。
思路:两点确定一条直线,如果剩余的其它点都在这条直线的同一侧,则这两个点是凸包上的点,否则就不是。
步骤:
将点集里面的所有点两两配对,组成 n(n-1)/2 条直线。
对于每条直线,再检查剩余的 (n-2) 个点是否在直线的同一侧。
如何判断一个点 p3 是在直线 p1p2 的左边还是右边呢?(坐标:p1(x1,y1),p2(x2,y2),p3(x3,y3))
利用叉积
(x2-x1)*(y3-y1)-(x3-x1)*(y2-y1)当上式结果为正时,p3在直线 p1p2 的左侧;当结果为负时,p3在直线 p1p2 的右边。
解二:分治法
时间复杂度:O(n㏒n)。
思路:应用分治法思想,把一个大问题分成几个结构相同的子问题,把子问题再分成几个更小的子问题……。然后我们就能用递归的方法,分别求这些子问题的解。最后把每个子问题的解“组装”成原来大问题的解。
步骤:
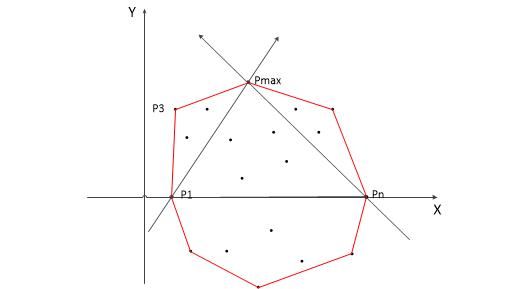
把所有的点都放在二维坐标系里面。那么横坐标最小和最大的两个点 P1 和 Pn 一定是凸包上的点(为什么呢?用反证法很容易证明,这里不详讲)。直线 P1Pn 把点集分成了两部分,即 X 轴上面和下面两部分,分别叫做上包和下包。
对上包:求距离直线 P1Pn 最远的点,即下图中的点 Pmax 。
作直线 P1Pmax 、PnPmax,把直线 P1Pmax 左侧的点当成是上包,把直线 PnPmax 右侧的点也当成是上包。
重复步骤 2、3。
对下包也作类似操作。
然而怎么求距离某直线最远的点呢?我们还是用到解一中的公式:
(x2-x1)*(y3-y1)-(x3-x1)*(y2-y1)
设有一个点 P3 和直线 P1P2 。(坐标:p1(x1,y1),p2(x2,y2),p3(x3,y3))
对上式的结果取绝对值,绝对值越大,则距离直线越远。
注意:在步骤一,如果横坐标最小的点不止一个,那么这几个点都是凸包上的点,此时上包和下包的划分就有点不同了,需要注意。
解三:Jarvis步进法
时间复杂度:O(nH)。(其中 n 是点的总个数,H 是凸包上的点的个数)
思路:
纵坐标最小的那个点一定是凸包上的点,例如图上的 P0。
从 P0 开始,按逆时针的方向,逐个找凸包上的点,每前进一步找到一个点,所以叫作步进法。
怎么找下一个点呢?利用夹角。假设现在已经找到 {P0,P1,P2} 了,要找下一个点:剩下的点分别和 P2 组成向量,设这个向量与向量P1P2的夹角为 β 。当 β 最小时就是所要求的下一个点了,此处为 P3 。
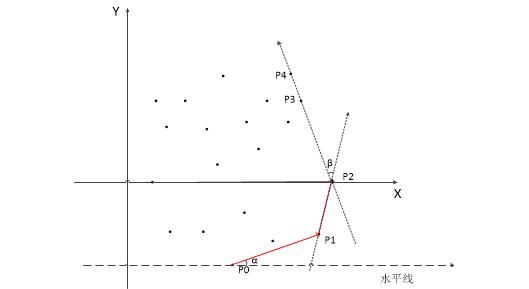
注意:
找第二个点 P1 时,因为已经找到的只有 P0 一个点,所以向量只能和水平线作夹角 α,当 α 最小时求得第二个点。
共线情况:如果直线 P2P3 上还有一个点 P4,即三个点共线,此时由向量P2P3 和向量P2P4 产生的两个 β 是相同的。我们应该把 P3、P4 都当做凸包上的点,并且把距离 P2 最远的那个点(即图中的P4)作为最后搜索到的点,继续找它的下一个连接点。
解四:Graham扫描法
时间复杂度:O(n㏒n)
思路:Graham扫描的思想和Jarris步进法类似,也是先找到凸包上的一个点,然后从那个点开始按逆时针方向逐个找凸包上的点,但它不是利用夹角。

步骤:
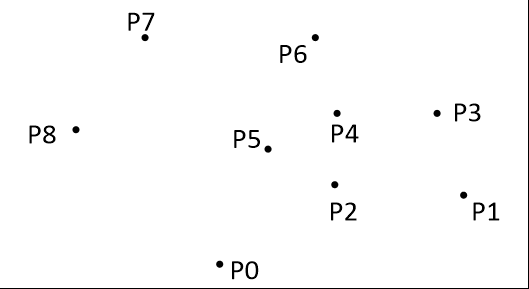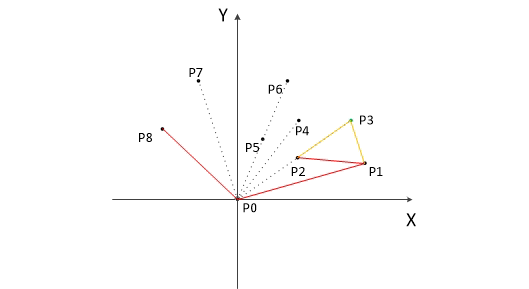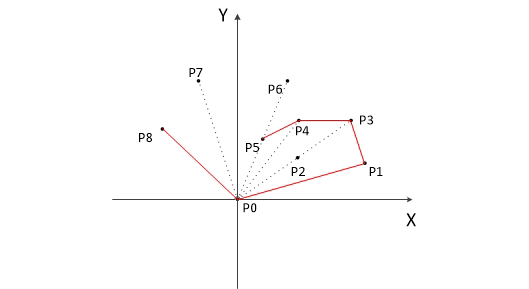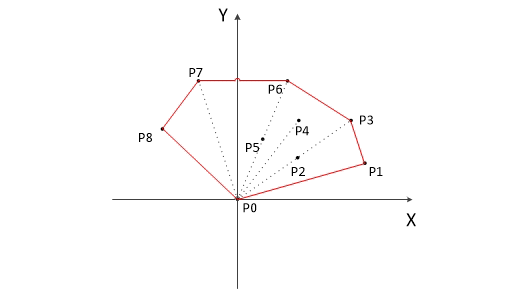
把所有点放在二维坐标系中,则纵坐标最小的点一定是凸包上的点,如图中的P0。
把所有点的坐标平移一下,使 P0 作为原点,如上图。
计算各个点相对于 P0 的幅角 α ,按从小到大的顺序对各个点排序。当 α 相同时,距离 P0 比较近的排在前面。例如上图得到的结果为 P1,P2,P3,P4,P5,P6,P7,P8。我们由几何知识可以知道,结果中第一个点 P1 和最后一个点 P8 一定是凸包上的点。
(以上是准备步骤,以下开始求凸包)
以上,我们已经知道了凸包上的第一个点 P0 和第二个点 P1,我们把它们放在栈里面。现在从步骤3求得的那个结果里,把 P1 后面的那个点拿出来做当前点,即 P2 。接下来开始找第三个点:
连接P0和栈顶的那个点,得到直线 L 。看当前点是在直线 L 的右边还是左边。如果在直线的右边就执行步骤5;如果在直线上,或者在直线的左边就执行步骤6。
如果在右边,则栈顶的那个元素不是凸包上的点,把栈顶元素出栈。执行步骤4。
当前点是凸包上的点,把它压入栈,执行步骤7。
检查当前的点 P2 是不是步骤3那个结果的最后一个元素。是最后一个元素的话就结束。如果不是的话就把 P2 后面那个点做当前点,返回步骤4。
最后,栈中的元素就是凸包上的点了。
以下为用Graham扫描法动态求解的过程:
#include<stdio.h>
#include<math.h>
#include<algorithm>
using namespace std;
int n,top;
struct point
{
int x,y;
} p[1005],s[1005],t;
double cross(point t1,point t2,point t3,point t4) //求向量t1t2和向量t3t4的叉积
{
return (t2.x-t1.x)*(t4.y-t3.y)-(t2.y-t1.y)*(t4.x-t3.x);
}
double dis(point t1,point t2) //求距离
{
double z=(t2.x-t1.x)*(t2.x-t1.x)+(t2.y-t1.y)*(t2.y-t1.y);
return sqrt(z);
}
bool cmp(point t1,point t2)
{
double z=cross(p[0],t1,p[0],t2);
return z?z>0:dis(p[0],t1)>dis(p[0],t2);
}
void findpoint() //找基点,按y从小到大,如果y相同,按x从左到右
{
int i,j=0;
t=p[0];
for(i=1; i<n; i++)
{
if(t.y>p[i].y||(t.y==p[i].y&&t.x>p[i].x))
{
j=i;
t=p[i];
}
}
t=p[0];
p[0]=p[j];
p[j]=t;
}
void scanner()
{
int i;
findpoint();
sort(p+1,p+n,cmp);
s[0]=p[0];
s[1]=p[1];
top=1;
for(i=2; i<n; i++)
{
while(cross(s[top-1],s[top],s[top],p[i])<0)
top--;
top++;
s[top]=p[i];
}
}
int main()
{
int i;
double ans;
while(~scanf("%d",&n))
{
for(i=0; i<n; i++)
{
scanf("%d%d",&p[i].x,&p[i].y);
}
scanner();
for(i=0; i<=top; i++)
{
printf("(%d,%d)\n",s[i],s[(i+1)%(top+1)]);
}
}
return 0;
}
/*
输入
14
30 30
50 60
60 20
70 45
86 39
112 60
200 113
250 50
300 200
130 240
76 150
47 76
36 40
33 35
输出
(60,20)
(250,50)
(300,200)
(130,240)
(76,150)
(47,76)
(30,30)
*/
解五:Melkman算法
Melkman算法迄今为止最好的凸包算法了,我强烈推荐的算法。它的基本操作和Graham-Scan一样,只不过它在任意时候都求得当前已考察点所形成的凸包,所以它有一个无可比拟的优势就是它是一个在线算法(要想往点集中增加一个点不必重新计算)。对于给定一个多边形,它可以直接求其凸包而不用先有序化。但对于点集,还是要先排序再用Melkman算法。
0. 初始化:排序各点,向双头表d中装入P2,P0,P1,P2;设双头表左右指针分别为b,t;
1.反复做i=i+1,直到d[t+1],d[t],Pi不做左转或d,d[b+1],Pi不做左转
2.做以下这些直到d[t+1],d[t],Pi做左转
t=t-1;
将Pi从右压入d;
做以下这些直到d,d[b+1],Pi做左转
b=b+1;
将Pi从左压入d
代码实现:
#include<stdio.h>
int g_result[240][2];
/*getResult()实现功能:以坐标P0(x1,y1)和Pn(x2,y2)为直线,找出pack里面里这条直线最远的点Pmax
*并找出直线P0Pmax和PmaxPn的上包,进行递归。
*注:Pack[0][0]存放点的个数,pack[1]开始存放点的坐标。
*全局变量g_result[][]用来存放凸包上的点,即最终所要的答案。同样g_result[0][0]存放的是已找到的点的个数。
**/
void getResult(int Pack[240][2], int x1, int y1, int x2, int y2)
{
int i,t,x3,y3,R,Rmax,tmax;
int ResultPack[240][2];
ResultPack[0][0] = 0;
if(Pack[0][0] <= 1)
return;
x3 = Pack[1][0];
y3 = Pack[1][1];
R = x1*y2 + x3*y1 + x2*y3 - x3*y2 - x2*y1 - x1*y3;
Rmax = R;
tmax = 1;
for(i=2;i<=Pack[0][0];i++)
{
x3 = Pack[i][0];
y3 = Pack[i][1];
R = x1*y2 + x3*y1 + x2*y3 - x3*y2 - x2*y1 - x1*y3;
if(R >= 0)
{
t = ++ResultPack[0][0];
ResultPack[t][0] = x3;
ResultPack[t][1] = y3;
}
if(R > Rmax)
{
Rmax = R;
tmax = i;
}
}
if(Rmax <= 0)
{
for(i=1;i<ResultPack[0][0];i++)
{
x3 = ResultPack[i][0];
y3 = ResultPack[i][1];
R = x1*y2 + x3*y1 + x2*y3 - x3*y2 - x2*y1 - x1*y3;
if(R == 0 && !((x3==x2&&y3==y2)||(x3==x1&&y3==y1)))
{
t = ++g_result[0][0];
g_result[t][0] = ResultPack[i][0];
g_result[t][1] = ResultPack[i][1];
}
}
return;
}
else
{
t = ++g_result[0][0];
g_result[t][0] = Pack[tmax][0];
g_result[t][1] = Pack[tmax][1];
if(ResultPack[0][0] == 0)
return;
}
getResult(ResultPack,x1,y1,Pack[tmax][0],Pack[tmax][1]);
getResult(ResultPack,Pack[tmax][0],Pack[tmax][1],x2,y2);
}
int main()
{
int Point[240][2];//Point存所有点。
int i=1,n;
int x1,y1,x2,y2,x3,y3;
g_result[0][0]=0;Point[0][0]=0;//Point的第一行第一列元素存放包里面有几个点。初始化为0。
printf("请输入所有点的个数及坐标:\n");
scanf("%d",&n);
for(i=1;i<=n;i++)
scanf("%d%d",&Point[i][0],&Point[i][1]);
Point[0][0] = i-1;
x1 = Point[1][0];
y1 = Point[1][1];
x2 = x1;
y2 = y1;
for(i=2;i<=Point[0][0];i++)
{
x3 = Point[i][0];
y3 = Point[i][1];
if(x3 < x1)
{
x1 = x3;
y1 = y3;
}
else if(x3 > x2)
{
x2 = x3;
y2 = y3;
}
}
g_result[1][0] = x1;
g_result[1][1] = y1;
g_result[2][0] = x2;
g_result[2][1] = y2;
g_result[0][0] += 2;
getResult(Point, x1, y1, x2, y2);
getResult(Point, x2, y2, x1, y1);
printf("\n\n构成凸包的点有:\n");
for(i=1;i<=g_result[0][0];i++)
printf("(%d,%d)\n",g_result[i][0],g_result[i][1]);
}
/* 输入
14
30 30
50 60
60 20
70 45
86 39
112 60
200 113
250 50
300 200
130 240
76 150
47 76
36 40
33 35
输出
(30,30)
(300,200)
(130,240)
(76,150)
(47,76)
(250,50)
(60,20)
*/
扩展:
以上讨论的只是二维的凸包,二维凸包可以用来解决围栏问题、城市规划问题、聚类分析等等。