关联规则挖掘

 一、初步理解  

关联规则是数据挖掘技术的一个活跃的研究方向之一，其反映出项目集之间有意义的关联关系。关联规则可以广泛地应用于各个领域，既可以检验行业内长期形成的知识模式，也能够发现隐藏的新规律。有效地发现、理解和运用关联规则是数据挖掘任务的一个重要手段。

在处理大量数据时，很重要的一点是要理解不同实体间相互关联的规律。通常，发现这些规律是个极为复杂的过程。关联规则是一种十分简单却功能强大的、描述数据集的规则，这是因为关联规则表达了哪些实体能同时发生。

关联规则的传统应用多见于零售业（适用于线下而非线上）。关联规则挖掘的一个典型例子是购物篮分析。该过程通过发现顾客放入其购物篮中不同商品之间的联系，分析顾客的购买习惯。通过了解哪些商品频繁地被顾客同时购买，这种关联的发现可以帮助零售商指定营销策略。例如，在同一次去超市，如果顾客购买牛奶，他也购买面包（包括什么类型的面包）的可能性有多大？通过帮助零售商有选择地经销和安排货架，这种信息可以引导销售。例如，将牛奶和面包尽可能放近一些，可以进一步的刺激一次去商店同时购买这些商品。全球最大的零售商沃尔玛(Walmart)通过对顾客购物清单的数据挖掘发现了“尿布→啤酒”的关联规则，后来沃尔玛就把尿布和啤酒摆放在一起，从而双双促进了尿布和啤酒的销量。

关联规则的另一应用领域是健康医疗，利用关联规则找出经常同时发生的健康问题，以便诊断出患一种疾病的患者还可能进行额外的检查，从而判断该患者是否存在其他与此疾病经常连带发生的身体问题。

        其他应用领域还包括入侵检查、web日志分析、数据库访问模式、文档抄袭检测等等。

二、关联规则的概念

设是项的集合。设任务相关的数据D是数据库事务的集合，其中每个事务T是项的集合，使得。每个事务有一个标识符，称作TID。

2.1 相关定义

支持度定义：假设有个支持度阀指（support threshold) s。 如果A是一个项集，A的支持度是指包含I的事务数目。或者是包含I的事务数目与总事务数的百分比。如果支持度不小于s，则称A是频繁项集(frequent itemset)。

  A的支持度(support)= 包含A的事务数 或者 包含A的事务数/总的事务数

2.2 关联规则(association rule)定义

关联规则的形式为A->j,其中A是一个项集，而j是一个项。该关联规则的意义为，如果A中所有项出现在某个事务中的话，那么j“有可能”也出现在这一事务中。

这个“有可能”可以通过定义规则的可信度/置信度(confidence)来形式化的给出。

A->j的可信度(confidence) = A∪j 的支持度/A的支持度

但是如果包含A的购物篮中包含j的概率等于所有购物篮中包含j的概率， 比较极端的是实际上所有的购物篮（事务）都包含j,那么即使A包含j的概率为100% 也是没有意义的，为了区分出这种A对j的兴趣度衡量。

    A->j的兴趣度(interest) = A->j的可信度 - j的支持度

当这个值很高或者是绝对值很大的负值都是具有意义的。前者意味着购物篮中A的存在在某种程度上促进了j的存在，而后者意味着A的存在会抑制j的存在。

        同时满足最小支持度阈值(min_sup)和最小置信度阈值（min_conf）的规则称作强规则。

        项的集合称为项集（itemset）。包含k个项的项集称为k-项集。集合{computer，financial_management_software}是一个2-项集。

       识别有用的关联规则并不比发现频繁项集难很多，以为他都是以支持度为基础的。实际当中，对于传统的零售商店的销售而言，“相当地高”大概相当于所有购物篮的1%左右。

三、预选算法与数据结构的数学分析

我们假定购物篮组成的文件太大以至于无法在内存中存放。因此，任何算法的主要时间开销都集中在将购物篮或者事务从磁盘读入内存这个过程。。

3.2 项集计数中内存使用

   当对数据进行一遍扫描时，所有的频繁项集算法要求我们必须在内存中维护很多不同的计数值。例如，我们必须要记录每两个项咋购物篮中出现次数。如果没有足够内存来存放这些数字，那么随机对其中的一个数字加1都很有可能需要将一个页面从磁盘载入到内存，如果这样，算法就会发生内存抖动现象。从而运行速度可能会比从内存中直接找到这些数字慢好几个数量级。所以结论是，我们不能对不能放入内存的任何对象计数。因此，每个算法必须有个能处理的项数目的上限。

例如：假定项目总数目n, 并且算法会计算所有项对的数目。因此，我们需要空间存储（n 2)及C2 20 = n的平方/2个整数，如果每个整数需要4字节，总共需要2n pow 2个字节。如果我们的机器有2GB即2 pow 31字节内存，那么必须要求n<=2pow 15。

如果项是字符串，可以表示为1-n上的整数。如果项没有采用这种表示方法，我们就需要哈希表将他们从文件中的表示形式转化为整数。如果该项已经存在，那么就可以从哈希表中获得其对应的整数码，如果不存在，那么就将下一个可用的数字赋给它，并将项及其整数码放入到哈希表中。(当然简单一点，并且可以通过哈希函数映射到不同的连续的整数空间上，这个哈希表不需要实际的存在，因为哈希函数的规则能够正确帮助我们找到这个整数码，这个整数码也就转换为项对的存放地址)

哈希表1 如bread-0

        apple-1

        beer -2......

3.2.1 三角矩阵方法(triangular matrix)

    在将项都编码成整数之后，我们可以使用三角矩阵来存放计数结果，i<j,a[i,j]。对每一个对需要空间一个integer = 4 bytes

   但是这种策略会使得数组的一般元素都没有使用。一个更节省空间的方法是使用一个一维的三角数组(trangular array）。

有1<=i<=j<=n,k=(i-1)(n-i/2)+(j-i)。即{i,j}对应为a[k]。这种布局相当于将所有的项对按照字典顺序排序，即一开始是｛1，2｝，｛1，3｝，。。。，｛1，n｝，｛2，3｝，｛2，4｝，。。。｛2，n}。。。｛n-1，n｝。

  这种当时分配的空间是已经确定的，为n-1+n-2+.....+1

3.2.2 三元组方法

  另一种有可能更加适合的存储计数值的方法为三元组[i,j,c]，即对{i,j}对的计数值c（i<j）。对每一个对需要空间3*integer =12 bytes

具体操作为采用类似哈希表的数据结构，其中i,j是搜索键值，这样就能确定对于给定的i,j是否存在对应的三元组，如果是则快速定位。这种方式我们称为存储数值的三元组方式(triples method)。

与三角矩阵的方式不同，如果某个项对（候选项对）的计数值为0，则三元组方式可以不用存储这个值，即只有C>0的才需要分配空间去存储。

   结论如下：

如果所有可能出现的（n 2）个项对中有至少1/3出现在购物篮的情况下，三角矩阵方式更优。而如果出现的比例显著小于1/3，那么就要考虑使用三元组方式。

3.2.3 二元组计数

实际当中可能很大的计算复杂性都在二元组，可能二元组的数目更多，所以上面的方法都是用来处理二元组。

四、A-Priori算法

 关联规则中最著名的算法当数Apriori算法。

   

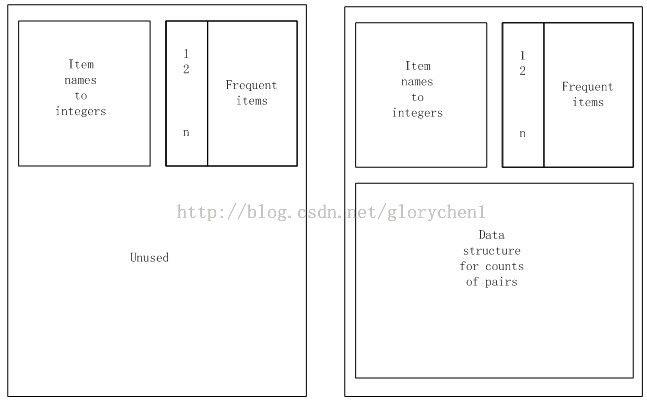
图1、Apriori算法的内存的使用情况，左边为第一步时的内存情况，右图为第二步时内存的使用情况

五、A-Priori算法的改进

下面具体介绍几个Apriori算法的改进算法，这些算法可以用在海量数据上的关联规则挖掘中。

（1）基于hash的方法。一个高效地产生频集的基于杂凑(hash)的算法由Park等[3]提出来。通过实验可以发现寻找频集主要的计算是在生成频繁2-项集Lk上，Park等就是利用了这个性质引入杂凑技术来改进产生频繁2-项集的方法。

（2）基于划分的方法。Savasere等[2]设计了一个基于划分(partition)的算法. 这个算法先把数据库从逻辑上分成几个互不相交的块，每次单独考虑一个分块并对它生成所有的频集，然后把产生的频集合并，用来生成所有可能的频集，最后计算这些项集的支持度。这里分块的大小选择要使得每个分块可以被放入主存，每个阶段只需被扫描一次。而算法的正确性是由每一个可能的频集至少在某一个分块中是频集保证的。

（3）基于采样的方法。基于前一遍扫描得到的信息，对此仔细地作组合分析，可以得到一个改进的算法，Mannila等[4]先考虑了这一点，他们认为采样是发现规则的一个有效途径。

5.1 基于hash的方法

        首先是基于哈希的算法。基于哈希的算法仍是将所有所有数据放入内存的方法。只要在计算的过程中能够满足算法对内存的大量需求，Apriori算法能够很好的执行。但在计算候选项集时特别是在计算候选项对C2时需要消耗大量内存。针对C2候选项对过大，一些算法提出用来减少C2的大小。这里我们首先考虑PCY算法，这个算法使用了在Apriori算法的第一步里大量没使用的内存。接着，我们考虑Multistage算法，这个算法使用PCY的技巧，但插入了额外的步骤来更多的减少C2的大小。

  Park，Chen，Yu（PCY）算法[3]：

        这个算法我们叫PCY算法，取自它的作者名字缩写。该算法关注在频繁项集挖掘中的第一步有许多内存空间没被利用的情况。如果有数以亿计的项，和以G计的内存，在使用关联规则的第一步里我们将会仅仅使用不到10%的内存空间，会有很多内存空闲。因为在第一步里，我们只需要两个表，一个用来保存项的名字到一个整数的映射，用这些整数值代表项，一个数组来计数这些整数，如图1。PCY算法使用这些空闲的内存来保存一个整数数组。其思想显示如图2。.将这个数组看做一个哈希表，表的桶中装的是整数值而不是一组key值。项对被哈希到这些桶中。在第一步扫描篮子的处理中，我们不但将这些项对加一，并且通过两步循环，我们创造出所有的项对。我们将项对哈希到哈希表中，并且将哈希到的位置加一。注意，项本身不会进入桶，项对的加入只是影响桶中的整数值。

        在第一步的结尾，每个桶中装有一个数字，这个数字表达了桶中的项对的数目。如果桶中数字大于支持度阈值s，这个桶被称为频繁桶。对于频繁桶，我们不能确定其项对是否为频繁项对，但有可能是。但是，对于阈值低于s的桶，我们知道其中的项对肯定不是频繁项对，即使项对是由两个频繁项组成。这个事实给我们在第二部处理带来很大的方便。我们可以定义候选集C2为这样的项对{i, j}：

1.      i和j是频繁项

2.      {i，j}哈希到一个频繁桶

        第二个条件是PCY算法与A-Priori算法的区别所在。

        在步骤1中使用hash表可能并不能带来好处，这取决于数据大小和空闲内存大小。在最坏的情形下，所有的桶都是频繁的，PCY计算的项对与A-priori是一样的。然而，在通常的情况下，大多数的桶都是非频繁的。这种情况下，PCY算法降低了第二步内存的使用。

        假设我们有1G的内存可用来在第一步做hash表存放，并假设数据文件包含在10亿篮子，每个篮子10个项。一个桶为一个整数，通常定义为4个字节，于是我们可以保存2.5亿个桶。所有篮子的项对的数量总数为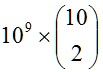或个。这个数量也是桶中计数的总和。这样，每个桶的平均计数为，或180个。所以，如果支持度阈值s在180附近，或更小，可能只有很少的桶是非频繁的。然而，当s足够大，比方说1000，这样会使大部分的桶成为非频繁的。这样最大可能的频繁桶数为，或450亿个频繁桶。

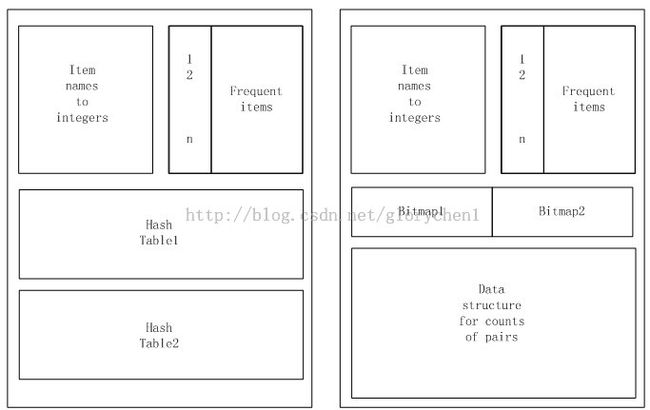
        在PCY算法中，在其第二步操作前，哈希表被压缩为bitmap，在这里，每一个bit用作一个桶。若桶为频繁桶，则位置1，否则置0。这样32bit的整数被压缩为只有1bit。然后再PCY的第二步操作中，bitmap只占了原来所用空间的1/32，如图2所示。如果大部分的桶都是非频繁桶，我们可以预料，在第二步的项对计数后产生的频繁项集会更小。这样，PCY算法就能直接在内存中处理这些数据集而不会耗尽内存。

        虽然在寻找频繁项对时，PCY算法与Apriori算法相差很大，但是，在三元对和更多元时，他们的方法又为相同了。

 

图2、使用PCY算法的内存组织形式，左图为步骤1的内存使用情况，右图为步骤2的内存使用情况

5.2 Mutistage 算法：

        Multistage算法是在PCY算法的基础上使用一些连续的哈希表来进一步降低候选项对。相应的，Multistage需要不止两步来寻找频繁项对。Multistage算法的框图描述在图3中。

       Multistage的第一步跟PCY的第一步相同。在第一步后，频繁桶集也被压缩为bitmap，这也和PCY相同。但是在第二步，Multistage不计数候选项对。而是使用空闲主存来存放另一个哈希表，并使用另一个哈希函数。因为第一个哈希表的bitmap只占了1/32的空闲内存，第二个哈希表可以使用几乎跟第一个哈希表一样多的桶。

       在Multistage的第二步，我们同样是需要遍历篮子文件。只是这步不需要再数项了，因为已经在第一步做了。但是，我必须保留那些项是频繁项的信息，因为我们需要它在第二步和第三步中。在第二步中，我们哈希哈希某些项对到第二个哈希表的桶中。一个对被哈希仅当它满足一下两条条件，即：如果i和j都是频繁的且它们在第一步被哈希到频繁桶中。这样，第二个哈希表中的计数总数将比第一步明显减少。

因此，即便是在第二步是由于第一步的bitmap占据了1/32的空闲空间，剩下的空间也照样够第二步的hash表使用。

        在第二步完成后，第二个hash表同样被压缩成bitmap。该bitmap也同样保存在内存中。这时，两个bitmap加起来也只占到不到空闲内存的1/16，还有相当的内存可用来做第三步的计算候选频繁项对的处理。一个相对{i，j}在C2中，当且仅当满足：

1、  i和j都是频繁项

2、  {i，j}在第一步哈希时被哈希到频繁桶中

3、  {i，j}在第二步哈希时被哈希到频繁桶中

        第三条是Multistage方法和PCY方法的主要区别。

        很显然，在算法中可用在第一步和最后一步中添加任意多的中间步骤。这里的限制就是在每一步中必须用一个bitmap来保存前一步的结果。最终这里会使得没有足够的内存来做计数。不管我们使用多少步骤，真正的频繁项对总是被哈希到一个频繁桶中，所以，这里没有方式来避免对它们计数。

 

图3、Multistage算法使用额外的哈希表来减少候选项对，左图为第一步内存使用情况，中图为第二步内存使用情况，右图为第三步内存使用情况

5.3 Multihash 算法

        有时我们从multistage算法的额外的步骤中获取好处。这个PCY的变形叫做Multihash[7]算法。不同于在连续的两个步骤中使用两个哈希表，该算法在一步中使用两个哈希算法和两个分离的哈希表。如表6.7所述。

        在同一步里使用两个hash表的危险是每个哈希表仅有PCY算法的一半的桶。只要PCY算法的桶的平均计数比支持度阈值低，我们就可以预见大部分的桶都是非频繁桶，并可以在这两个只有一半大小的哈希表上操作完成。在这种情形下，我们选择multihash方法。

        对Multihash的第二步，每个hash表也会被转换为一个bitmap。注意，在图6.7中，两个bitmap占据的空间只有PCY算法的一个bitmap的大小。项对{i，j}被放入候选集C2的条件同multistage：i和j必须是频繁的，且{i，j}对在两个哈希表中必须被hash到频繁桶。

        正如Multistage算法，在Multihash算法中，我们也可以不用限制只使用两个hash表。在Multihash算法的第一步中，我们也可以使用多个hash表。不过风险是桶的平均计数会超过阈值。在这种情况下，这里会只有很少的非频繁桶在每个hash表中。即使这样，一个项对必须被hash到每个hash表的频繁桶中并计数，并且，我们会发现，一个非频繁项对作为一个候选的概率将上升，而不是下降，无利反而有害。

 

 

图3、Multihash算法使用多个hash表在第一步中，左图为第一步处理，右图为第二步处理

       使用两个哈希表的危险是在第一步，每个哈希表仅有PCY哈希表的一半的桶容量。只要PCY桶的平均数目比支持的阈值低，我们就能操作两个一半大小的哈希表，其期望哈希表的大多数桶不是频繁的。这样，在这种情形下，我们可以选择multihash方法。

5.4 基于采样的方法

       前面所讨论的频繁项都是在一次能处理的情况。如果数据量过大超过了主存的大小，这就不可避免的得使用k步来计算频繁项集。这里有许多应用并不需要发现所有的频繁项。比方说在超市，我们只要找到大部分的销售频繁关联项就够了，而不必找出所有的频繁项。

        在这一节，我们介绍几种算法来找到所有或大部分的项集使用两步。我们首先从使用一个简单的数据样本开始，而不是整个数据集。一个算法叫做SON，使用两步，得到精确结果，并使得它能够在map-reduce和其他并行处理的框架下运行。最后，Toivonen的算法平均使用两步获取精确结果，但是，可能但不是经常不能在给定的时间内完成。

一个简单的随机算法

        不是使用整个文件或篮子，我们使用篮子的一个子集并加装他们是整个数据集。我们必须调整支持度的阈值来适应我们的小篮子。例如，我们针对完整数据集的支持度阈值为s，当我们选择1%的样本时，我们可以在支持度阈值为s/100的度量上测试。

        最安全的抽样方式是读入整个数据集，然后对于每个篮子，使用相同的概率p选择样品。假设这有m个篮子在整个文件中。在最后，我们需要选择的样品的数量接近pm个篮子的样品数。如果我们事先知道这些篮子本身在文件中就是随机放置的，那么我们就可以不用读入整个文件了，而是只接选择前面的pm个篮子作为样品就可以了。或在，如果文件是分布式文件系统，我们可以选择第一个随机块作为样品。

       当我们的样品选择完成，我们可以使用部分的主存来放置这些篮子。剩下的主存用来执行前面的Apriori、PCY、Multistage或Multihash算法。当然这些算法必须运行所有的样品，在每个频繁集上，直到找不到频繁集为止。这个方法在执行读取样品时不需要磁盘操作，因为它是驻留在内存的。当每个频繁项被发现，它们就可以写到磁盘上了；这个操作和最初的读样品到内存是唯一的两次磁盘操作。当然若读入样品后剩下的内存不够执行之前所说的算法时，这种方法会失败。当然，可以选择在算法的每步完成后写到磁盘再仅从磁盘调入下步所需的数据。因为样品的数量相比与整个文件是很小的，所以，I/O操作的代价还是很小的。

 

避免错误的抽样算法

        我们需要知道在简单抽样方法中可能出现错误。因为我们使用的是抽样，所有就可能存在是频繁项的没有放进频繁集，也存在非频繁项的放入了频繁集。

        当样本足够大时，问题变得不是那么严重了。这时，那些支持度远大于阈值的项集即使在样本中其支持度也会很高，所有误分的可能性不大。但是那些支持度在阈值附近的就不好说了。很有可能由于抽样使得支持度稍微改变而改变对其是否是频繁集的判断

        我们可以通过一遍对整个数据集的扫描，计算所有样品中频繁项集的支持度，保留那些在样品中和在数据集上支持度都高于阈值的频繁项集。以此避免非频繁项集被判为频繁项集的错误。值得注意的，这种方法不能避免那些是频繁集却被当做非频繁项集的情况。

        我们不能消除那些是频繁项集却没有在样品中找出的情况，但是我们可以减少它们的数量如果内存的数量允许。我们设想如果s是支持阈值，且样品相对于整个数据集的大小为p，这样我们可以使用ps作为支持阈值。然而我们可以使用比这个值稍微小点的值作为阈值，如0.9ps。使用更低的阈值的好处是能使更多的项进入到频繁集中，这样就可以降低这种错误，然后再以这些频繁项集到整个数据集中计算支持度，除去那些非频繁项集，这样我们就可以消除非频繁项集当成频繁项集的错误，同时最大化的减少了频繁项集被当做了非频繁项集。

Toivonen的算法[8]

        这个算法给出另一种不同的随机抽样算法。Toivonen算法在给出足够内存的情况下，在小样本上进行一步处理，接着再整个数据上进行一步处理。这个算法不会带来false negatives，也不会带来false positives，但是这里存在一个小的概率使得算法会产生不了任何结构。这种情况下算法需要重复直至找到一个结果，虽然如此，得到最终频繁项集的处理的平均步数不会太大。

        Toivonen算法由从输入数据集中选择一个小的样品开始，并从中找到候选频繁项集，找的过程同Apriori算法，不过很重要的一点不同是阈值的设置的比样品比例的阈值小。即，当整个数据集上的支持度阈值为s，该样品所占数据集的比例为p，则该阈值可以设置为0.9ps或0.8ps。越小的阈值，就意味着在处理样本时，越多的内存在计算频繁项集时需要使用；但是也就越大的可能性避免算法不能产生结果。

        当样本的频繁项集被构造完成后，我们的下一步是构造negative border。这是样品的一个非频繁项集合，但是这些项集的任意去掉一个项后就是频繁集了。

        考虑项为{A,B,C,D,E}，而且我们找到频繁项集为{A}，{B}，{C}，{D}，{B，C}，{C，D}。注意，只要篮子数不比阈值小，Φ也是频繁的，但是我们忽略它。首先，{E}是在negative border中的，因为{E}本身不是频繁项集，但是从中去任意项后就变成Φ了，就成了频繁项集，所有包含在negative border中。

        还有{A，B}，{A，C}，{A，D}和{B，D}都在negative border中。因为它们都不是频繁项集，但是除掉一个项的子集都是频繁项集。如{A，B}的子集{A}和{B}都是频繁集。剩下的六个二元项集不在negative border中。{B，C}和{C，D}因为它们本身是频繁项集，所有就不是negative border的元素了，而其他四个虽然不是频繁项集，但是因为包含了项E，而子集{E}不是频繁项集

        没有任何三元的或更大的项集在negative border中了。例如{B，C，D}不在negative border中，因为它有一个立即子集{B，D}，而{B，D}不是频繁项集。这样，negative border由下面五个集合组成：{E}，{A，B}，{A，C}，{A，D}和{B，D}。

        为了完成Toivonen算法，我们需要一步在整个数据集上的处理，算出所有在样品中的频繁项集或negative border中的所有项集。这步会产生的可能输出为：

1、  negative border中没有一个项集在整个数据集上计算为频繁项集。这种情况下，正确的频繁项集就为样本中的频繁项集。

2、  某些在negative border中的项集在整个数据集中计算是频繁项集。这时，我们不能确定是否存在更大的项集，这个项集既不在样本的negative border中，也不在它的频繁项集中，但是是整个数据集的频繁项集。这样，我们在此次的抽样中得不到结果，算法只能在重新抽样，继续重复上面的步骤，直到出现满足输出情形1时停止。

为什么Toivonen算法可以奏效

        显然 Toivonen算法不会产生false positive，因为它仅仅将在样本中是频繁项并在整个数据集上计算确实为频繁项集的项集作为频繁项集。为讨论该算法能够不产生false negative，我们需要注意，在Toivonen算法中，没有negativeborder中的项集是频繁项集。所有，无论如何，不存在在整个数据集上是频繁的，而在样本中既不出现在频繁集中，也不出现在negative border中。

        给个反例。假设这里有个集合S在数据集上是频繁项集，但是既不在样本的negative border中，也不是样本的频繁项集。那么在Toivonen算法的一步结束后，产生结果，并且结果中的频繁项集合中没有S。由频繁项集的单调性知，S的所有子集都是整个数据集的频繁项集。假设T是S的一个在样本中不属于频繁项集的最小子集。

        我们说，T一定在negative border中。当然，T满足在negative border中的条件：它自己不是样本的频繁项集。而它的直接子集是样布的频繁项集，因为若不是，则T不是S的在样本中不属于频繁项集的最小子集，产生矛盾。

        这里我们可以发现T即是数据集的频繁项集，又在样本的negative border中。所有，我们对这种情况的Toivonen算法，让其不能产生结果。

5.5 基于划分的方法

        使用划分的方法是处理海量数据的管理规则的另一个有效的方法。不同于基于采样的方法，该方法能够对数据集上所有数据进行处理。

Savasere,Omiecinski, and Navathe算法[2]

        我们的下一个算法同时避免了false negatives和false positives，所带来的代价是需要两个完全的步骤。该算法叫做SON算法，为三个作者名字的简称。其思想是将输入文件划分成块(chunks)。将每个文件块作为一个样本，并执行Apriori算法在其块上。同样的使用ps作为其阈值。将每个块找到的频繁项集放到磁盘上。

        一旦所有的块按此方式被处理，将那些在一个或多个块中被选中的频繁项集收集起来作为候选频繁项集。注意，如果一个项集在所有的块中都不是频繁项集，即它在每个块中的支持度都低于ps。因为块数位1/p，所以，整体的支持度也就低于(1/p)ps=s。这样，每个频繁项集必然会出现在至少一个块的频繁项集中，于是，我们可以确定，真正的频繁项一定全在候选频繁项集中，因此这里没有false negatives。

        当我们读每个块并处理它们后，我们完成一次处理。在第二步处理中，我们计算所有的候选频繁项集，选择那些支持度至少为s的作为频繁项集。

 

SON算法与Map-Reduce

        SON算法使得它很适合在并行计算的环境下发挥功效。每个块可以并行的处理，然后每个块的频繁集合并形成候选集。我们可以将候选分配到多个处理器上，在每个处理器上，这些处理器只需要在一个“购物篮”子集处理这些发过来的候选频繁项集，最后将这些候选集合并得到最终的在整个数据集上的支持度。这个过程不必应用map-reduce，但是，这种两步处理的过程可以表达成map-reduce的处理。下面将介绍这种map-reduce-map-reduce流程。

        FirstMap Function：分配篮子子集，并在子集上使用Apriori算法找出每个项集的频繁度。将支持阈值降从s降低到ps，如果每个Map任务分得的部分占总文件的比例为p。map的输出为key-value对(F,1)，这里F为该样本的频繁项集。值总是为1，这个值是无关紧要的。

        FirstReduce Function：每个reduce任务被分配为一组key，这组key实际就为项集，其中的value被忽略，reduce任务简单产生这些出现过一次或多次的项集，将其作为候选频繁项集作为输出。

        SecondMap Function：第二步的map任务将第一步的reduce的所有输出和输入文件的一部分作为输入，每个Map任务计算在分配的那块输入文件中每个候选频繁项集的出现次数。这步的输出为键值对(C，v)，这里，C是一个候选集，v是其在该Map任务中的支持度。

        SecondReduce Function：此步的Reduce任务将在每个候选频繁项集各个Map中的候选集的支持度相加。相加的结果就为整个文件上的支持度，这些支持度若大于s，则保留在频繁项集中，否则剔除。

5.6 其他的频集挖掘方法

        上面我们介绍的都是基于Apriori的频集方法。即使进行了优化，但是Apriori方法一些固有的缺陷还是无法克服：

1. 可能产生大量的候选集。当长度为1的频集有10000个的时候，长度为2的候选集个数将会超过10M。还有就是如果要生成一个很长的规则的时候，要产生的中间元素也是巨大量的。
2. 无法对稀有信息进行分析。由于频集使用了参数minsup，所以就无法对小于minsup的事件进行分析；而如果将minsup设成一个很低的值，那么算法的效率就成了一个很难处理的问题。

        下面将介绍两种方法，分别用于解决以上两个问题。

        针对问题一，J.Han等在[5]中提出了不产生候选挖掘频繁项集的方法：FP-树频集算法。他们采用了分而治之的策略，在经过了第一次的扫描之后，把数据库中的频集压缩进一棵频繁模式树（FP-tree），同时依然保留其中的关联信息。随后我们再将FP-tree分化成一些条件库，每个库和一个长度为1的频集相关。然后再对这些条件库分别进行挖掘。当原始数据量很大的时候，也可以结合划分的方法,使得一个FP-tree可以放入主存中。实验表明，FP-growth对不同长度的规则都有很好的适应性，同时在效率上较之apriori算法有巨大的提高。

        第二个问题是基于这个的一个想法：apriori算法得出的关系都是频繁出现的，但是在实际的应用中，我们可能需要寻找一些高度相关的元素，即使这些元素不是频繁出现的。在apriori算法中，起决定作用的是支持度，而我们现在将把可信度放在第一位，挖掘一些具有非常高可信度的规则。Edith Cohen在[6]中介绍了对于这个问题的一个解决方法。整个算法基本上分成三个步骤：计算特征、生成候选集、过滤候选集。在三个步骤中，关键的地方就是在计算特征时Hash方法的使用。在考虑方法的时候，有几个衡量好坏的指数：时空效率、错误率和遗漏率。基本的方法有两类：Min_Hashing(MH)和Locality_Sensitive_Hashing(LSH)。Min_Hashing的基本想法是：将一条记录中的头k个为1的字段的位置作为一个Hash函数。Locality_Sentitive_Hashing的基本想法是：将整个数据库用一种基于概率的方法进行分类，使得相似的列在一起的可能性更大，不相似的列在一起的可能性较小。我们再对这两个方法比较一下。MH的遗漏率为零，错误率可以由k严格控制，但是时空效率相对的较差。LSH的遗漏率和错误率是无法同时降低的，但是它的时空效率却相对的好很多。所以应该视具体的情况而定。最后的实验数据也说明这种方法的确能产生一些有用的规则。

参考文献

1 R. Agrawal, T. Imielinski, and A. Swami. Mining association rules between sets of items in large databases. Proceedings of the ACM SIGMOD Conference on Management of data, pp. 207-216, 1993.

2 A. Savasere, E. Omiecinski, and S. Navathe. An efficient algorithm for mining association rules in large databases. Proceedings of the 21st International Conference on Very large Database, 1995
3 J. S. Park, M. S. Chen, and P. S. Yu. An effective hash-based algorithm for mining association rules. Proceedings of ACM SIGMOD International Conference on Management of Data, pages 175-186, San Jose, CA, May 1995.
4 H. Mannila, H. Toivonen, and A. Verkamo. Efficient algorithm for discovering association  rules. AAAI Workshop on Knowledge Discovery in Databases, 1994, pp. 181-192.
5 J.Han,J.Pei,and Y.Yin.Mining frequent patterns without candidate generation.In Proc.2000 ACM-SIGMOD Int.Conf.Management of Data(SIGMOD’00),Dalas,TX,May 2000.
6 Edith Cohen, Mayur Datar, Shinji Fujiwara, Aristides Gionis, Piotr Indyk, Rajeev Motwani, Jeffrey D.Ullman, Cheng Yang. Finding Interesting Associations without Support Pruning. 1999
7 M. Fang, N. Shivakumar, H. Garcia-Molina, R. Motwani, and J. D. Ullman, “Computing iceberg queries efficiently,” Intl. Conf. on Very Large Databases, pp. 299-310, 1998.
8 H. Toivonen, “Sampling large databases for association rules,” Intl. Conf. on Very Large Databases, pp. 134–145, 1996.