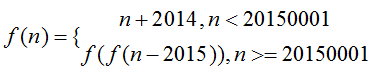fzu月赛(2015.11)
Problem Description
Sunday最近对图论特别感兴趣，什么欧拉回路什么哈密顿回路，又是环又是树。在看完一本书后，他对自己特别有信心，便找到大牛牛犇犇，希望他出一题来考考自己。
在遥远的古代东方有N个城市，它们之间可以通过双向的道路相连。任意两个城市由不超过一条道路直接相连，而且没有城市的道路连向自身。但是牛犇犇是个纯情的小伙子，尽管他还没有女朋友，但他还是很讨厌第三者，以至于讨厌三这个数字。所以他希望Sunday能够构造一个N个城市的地图，这个地图中不能有任意三个城市能够相互直接到达，而且地图中的道路数目最多。
牛犇犇考虑到Sunday是个菜鸟，所以只让他回答上述地图含有的道路数目，而不需要输出地图是由哪些道路组成。（题外话：其实只是因为special judge的评测程序比较麻烦而已）
Input
第一行一个整数T（1 <= T <= 100），表示测试数据的组数。
每组数据只包含一个N（1 <= N <= 1000），表示N个城市。
Output
每组数据输出仅有一行，表示在符合题意下N个城市所能连接的最大道路数目。
Sample Input
Sample Output
Source
FOJ有奖月赛-2015年11月
#include<stdio.h>
#include<string.h>
#include<math.h>
#include<queue>
#include<map>
#include<stack>
#include<vector>
#include<list>
#include<set>
#include<string>
#include<algorithm>
#pragma comment(linker, "/STACK:102400000, 102400000")
int f[1011];
void init(){
memset(f,0,sizeof(f));
f[1]=0,f[2]=1,f[3]=2,f[4]=4,f[5]=5;
for(int i=5;i<=1000;i++)
f[i]=f[i-1]+i/2;
}
int main(){
init();
int t,n;
scanf("%d",&t);
while(t--){
scanf("%d",&n);
printf("%d\n",f[n]);
}
return 0;
}
Problem Description
Input
Output
Sample Input
Sample Output
Source
FOJ有奖月赛-2015年11月
#include<stdio.h>
#include<string.h>
#include<math.h>
#include<queue>
#include<map>
#include<stack>
#include<vector>
#include<list>
#include<set>
#include<string>
#include<algorithm>
#pragma comment(linker, "/STACK:102400000, 102400000")
int main(){
int t;
scanf("%d",&t);
while(t--){
int n;
scanf("%d",&n);
if(n>=20150001){
printf("20152014\n");
}
else{
printf("%d\n",n+2014);
}
}
return 0;
}
Problem Description
小茗同学最近在认真地准备比赛，所以经常玩以撒的结合。
《以撒的结合》是一款由Edmund McMillen，Florian Himsl 开发，并由Edmund McMillen最早于2011年09月29日发行的一款2D平面角色扮演、动作冒险类的独立游戏。游戏的角色将在有着能够提升能力的道具与特殊技能的半RPG世界中闯荡。
——来自百度百科
小茗同学在打BOSS前，费掉了很多HP。在地图的一些房间里有补充HP的红心，然而小茗同学受到了看不见地图的诅咒。凭借不知道哪里来的记忆，小茗同学记得某个有红心的房间在房间A与房间B的路上的第K个房间里。为了简化问题，我们把地图看成一棵树。小茗同学想知道A到B的第K个房间号为多少，由于小茗同学很累，所以现在这个任务交给你了。
Input
第一行是一个整数T(T<=10)，表示有T组测试数据。
每组数据的第一行为两个整数n m(0<n<=1000,0<m<=n*n),分别表示房间个数和询问次数。
接下来n-1行，每行两个整数u v(0<u、v<=n，且u≠v),表示地图上房间u和房间v有一条路径。
最后是m行，每行三个整数u v k，表示询问房间u到房间v的路径上的第k个房间。
输入数据保证合法，即k不超过u、v的最短距离。
Output
对于每组数据，首先第一行先输出“Case #x:“ ，其中x是从1开始，表示数据组号，接下来m行，每行输出相应的房间号。
Sample Input
Sample Output
Source
FOJ有奖月赛-2015年11月
#include <stack>
#include <queue>
#include <cmath>
#include <ctime>
#include <vector>
#include <cstdio>
#include <cctype>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <algorithm>
using namespace std;
#define INF 0x3f3f3f3f
#define inf -0x3f3f3f3f
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define mem0(a) memset(a,0,sizeof(a))
#define mem1(a) memset(a,-1,sizeof(a))
#define mem(a, b) memset(a, b, sizeof(a))
const int MAXN=1110;
const int DEG=13;
struct Edge{
int to,next;
}e[MAXN*2];
int head[MAXN],tot;
void addedge(int u,int v){
e[tot].to=v;
e[tot].next=head[u];
head[u]=tot++;
}
void init(){
tot=0;
memset(head,-1,sizeof(head));
}
int fa[MAXN][DEG];
int deg[MAXN];
void bfs(int root){
queue<int>que;
deg[root]=0;
fa[root][0]=root;
que.push(root);
while(!que.empty()){
int tmp=que.front();
que.pop();
for(int i=1;i<DEG;i++)
fa[tmp][i]=fa[fa[tmp][i-1]][i-1];
for(int i=head[tmp];i!=-1;i=e[i].next){
int v=e[i].to;
if(v==fa[tmp][0])
continue;
deg[v]=deg[tmp]+1;
fa[v][0]=tmp;
que.push(v);
}
}
}
int LCA(int u,int v){
if(deg[u]>deg[v])
swap(u,v);
int hu=deg[u],hv=deg[v];
int tu=u,tv=v;
for(int det=hv-hu,i=0;det;det>>=1,i++)
if(det&1)
tv=fa[tv][i];
if(tu==tv)
return tu;
for(int i=DEG-1;i>=0;i--){
if(fa[tu][i]==fa[tv][i])
continue;
tu=fa[tu][i];
tv=fa[tv][i];
}
return fa[tu][0];
}
int Kth(int u,int k){
for(int i=12;i>=0;i--){
if(k>=(1<<i)){
k-=(1<<i);
u=fa[u][i];
}
}
return u;
}
int main(){
int t;
int n,m,u,v;
scanf("%d",&t);
for(int case1=1;case1<=t;case1++){
scanf("%d%d",&n,&m);
init();
for(int i=1;i<n;i++){
scanf("%d%d",&u,&v);
addedge(u,v);
addedge(v,u);
}
int k;
bfs(1);
printf("Case #%d:\n",case1);
for(int i=1;i<=m;i++){
scanf("%d%d%d",&u,&v,&k);
int w=LCA(u,v);
if(k==1)
printf("%d\n",u);
else if(deg[u]+deg[v]-2*deg[w]+1==k)
printf("%d\n",v);
else if(deg[u]-deg[w]+1>=k){
int ret=Kth(u,k-1);
printf("%d\n",ret);
}
else{
int x=deg[u]+deg[v]-2*deg[w]-k+1;
int ret=Kth(v,x);
printf("%d\n",ret);
}
}
}
return 0;
}
Problem Description
老S在某城市生活的非常不自在，想趁着ICPC举办期间在省内转转。已知老S所在的省有N个城市，M条无向边（对于某一对结点可能出现重边）。由于省内的交通相当糟糕，通过某条边所需要花费的时间受到一天中不同时刻的影响。此外对于某一时刻（一天24小时的任意一个整点算一个时刻），从任何方向通过无向边所需要的时间相同。现在老S想请你帮他规划一下旅行路线。
Input
第一行输入为一个整数T表示测试个数T
对于每一个测试的第一行为3个整数N，M，K，其中K表示老S的询问数
之后有2M行，一组2行共M组。每组第一行是两个整数x,y表示第x个城市与第y个城市之间有一条无向边。
每组第二行有24个整数cost[i](0<=i<=23)表示在第i个时刻通过这条无向边需要消耗的时间（单位为小时）。并且保证cost[i]<=coust[i+1]+1(0<=i<=22)且cost[23]<=cost[0]+1。
之后有K每行有两个整数D和S表示询问，从1号城市的第S个时刻出发，最终目的地为城市D所需要最少几个小时，此外如果老S不能到达目标城市则输出-1。
Limit:
1 <=x, y<=N.
1 <=all Cost values<=50.
1 <=D<=N.
0 <=S<=23.
1 <=T<=100.
2 <=N<= 20.
1 <=M<=100.
1 <=K<= 100.
Output
对于任意一个样例输出仅有一行包括"Case #x: "其中x表示第x个样例，之后有K个整数用空格分隔开，分别表示老S的K个询问的答案。
Sample Input
Sample Output
Source
FOJ有奖月赛-2015年11月
#include <stack>
#include <queue>
#include <cmath>
#include <ctime>
#include <vector>
#include <cstdio>
#include <cctype>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <algorithm>
using namespace std;
#define INF 0x3f3f3f3f
#define inf -0x3f3f3f3f
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define mem0(a) memset(a,0,sizeof(a))
#define mem1(a) memset(a,-1,sizeof(a))
#define mem(a, b) memset(a, b, sizeof(a))
const int maxn=30;
const int MAXN=50000;
struct Edge{
int to,next,cost;
}e[MAXN];
int head[maxn],dist[maxn],belong[MAXN];
int tot;
void addedge(int u,int v,int w,int i){
e[tot].to=v;
e[tot].cost=w;
e[tot].next=head[u];
belong[tot]=i;//i表示第几个时刻
head[u]=tot++;
}
void init(){
mem1(head);
tot=0;
}
int vis[maxn];
struct qnode{
int v;
int c;
qnode(int _v=0,int _c=0):v(_v),c(_c){}
bool operator <(const qnode &r) const{
return c>r.c;
}
};
void Dijkstra(int n,int w){
mem0(vis);
for(int i=1;i<=n;i++)
dist[i]=INF;
dist[1]=w;
priority_queue<qnode>que;
while(!que.empty())
que.pop();
que.push(qnode(1,dist[1]));
qnode tmp;
while(!que.empty()){
tmp=que.top();
que.pop();
int u=tmp.v;
if(vis[u]==1)
continue;
for(int i=head[u];i!=-1;i=e[i].next){
if(belong[i]==(dist[u]%24)){
int v=e[i].to;
int cost=e[i].cost;
if(!vis[u]&&dist[v]>dist[u]+cost){
dist[v]=dist[u]+cost;
que.push(qnode(v,dist[v]));
}
}
}
}
}
int main(){
int t,n,m,k;
scanf("%d",&t);
for(int case1=1;case1<=t;case1++){
scanf("%d%d%d",&n,&m,&k);
int u,v,w,to;
init();
for(int i=1;i<=m;i++){
scanf("%d%d",&u,&v);
for(int i=0;i<=23;i++){
scanf("%d",&w);
addedge(u,v,w,i);
addedge(v,u,w,i);
}
}
printf("Case #%d:",case1);
for(int i=1;i<=k;i++){
scanf("%d%d",&to,&w);
Dijkstra(n,w);
if(dist[to]==INF)
printf(" -1");
else
printf(" %d",dist[to]-w);
}
printf("\n");
}
return 0;
}
Problem Description
A国和B国正在进行一场战争，A国有n座城市，这些城市被m条有向道路相连，这些道路不会形成环路。其中有一部分城市比较特殊，其拥有粮仓，拥有粮仓的城市不能被其他城市到达，粮食可以从粮仓经过一些道路送往任意一座城市，现在B国的国王想要破坏一座A国的城市，粮食不能经过被破坏的城市。问破坏哪一座城市，可以使得最多的城市断粮。
Input
第一行两个数n和m(n<=1000,m<=10000)
接下来m行，每行两个数字a和b，表示城市a有一条连向城市b的道路
Output
输出一个数，表示被破坏的城市的序号，如果有多个城市满足条件，输出序号最小的那个城市
Sample Input
Sample Output
Source
FOJ有奖月赛-2015年11月
首先,明确一个概念,粮仓的地方是入度为0的点,所以可以统计入度为1的点有哪些点,然后统计这个点属于哪一个点，求出所属的点最多的那个点便可以了
#include<stdio.h>
#include<string.h>
#include<math.h>
#include<queue>
#include<map>
#include<stack>
#include<vector>
#include<list>
#include<set>
#include<string>
#include<algorithm>
#pragma comment(linker, "/STACK:102400000, 102400000")
int mp[1001][1001];
int belong[1001],count1[1001],count2[1001];
int main(){
int n,m;
while(scanf("%d%d",&n,&m)!=EOF){
for(int i=1;i<=n;i++)
for(int j=0;j<=n;j++)
mp[i][j]=0;
int u,v;
memset(count1,0,sizeof(count1));
memset(count2,0,sizeof(count2));
for(int i=1;i<=m;i++){
scanf("%d%d",&u,&v);
if(mp[u][v]==0){
mp[u][v]=1;
count1[v]++;
belong[v]=u;
}
}
for(int i=1;i<=n;i++){
if(count1[i]==1){
count2[belong[i]]++;
}
}
int maxv=0,ans;
for(int i=1;i<=n;i++){
if(count2[i]>maxv){
maxv=count2[i];
ans=i;
}
}
printf("%d\n",ans);
}
return 0;
}
Problem Description
小菇凉和小光头在提莫的蘑菇田里采走的蘑菇扇子妈妈很喜欢，所以小菇凉特地回来感谢提莫，并且教会它一种奇怪的黑暗魔法，可以使得某种蘑菇在固定的 Si 时刻种下后快速在 Ti 时刻成熟。双十一到了，提莫觉得很缺钱，所以他决定利用这个黑魔法尽可能多地种植出蘑菇换到更多的金币。
提莫有N块蘑菇田，他有M种蘑菇可以种植，同时刻中每块蘑菇田只能种植一种蘑菇，对于每种蘑菇只能种植一次，且第 i 种蘑菇只有在固定的 Si 到Ti 时间内种植才能使用黑魔法快速生长，并能用这个蘑菇田的收获换得 Vi 的金币。
提莫想知道他最多能获得多少金币。
特别的：对于某两种蘑菇 i 和蘑菇 j ，如果Sj==Ti，那么蘑菇 j 不能立即种植在蘑菇 i 所在田地上。
Input
输入共T(<=100)组数据。
输入第一行包括两个整数，N(<=50)，M(<=100)。 N为提莫总共有的蘑菇田的数目，M表示提莫可以种植的蘑菇种数。
接下来M行，每行三个整数 Si ， Ti 和 Vi (<2^31)表示第i种蘑菇能在 Si 到Ti 的时间内种植一次，收获换得Vi的钱币。
Output
输出一个整数( <2^31)表示提莫最多可获得的钱币。
Sample Input
Sample Output
Source
FOJ有奖月赛-2015年11月
最大费用最大流,把一个点拆成两个点,然后跑就可以了
#include <stack>
#include <queue>
#include <cmath>
#include <ctime>
#include <vector>
#include <cstdio>
#include <cctype>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <algorithm>
using namespace std;
#define INF 0x3f3f3f3f
#define inf -0x3f3f3f3f
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define mem0(a) memset(a,0,sizeof(a))
#define mem1(a) memset(a,-1,sizeof(a))
#define mem(a, b) memset(a, b, sizeof(a))
typedef long long ll;
const int MAXN=310;
const int MAXM=50110;
struct Edge
{
int to,next,cap,flow,cost;
}edge[MAXM];
int head[MAXN],tol;
int pre[MAXN],dis[MAXN];
bool vis[MAXN];
int N;//节点总个数，节点编号从0~N-1
void init(int n)
{
N = n;
tol = 0;
memset(head,-1,sizeof(head));
}
void addedge(int u,int v,int cap,int cost)
{
edge[tol].to = v;
edge[tol].cap = cap;
edge[tol].cost = cost;
edge[tol].flow = 0;
edge[tol].next = head[u];
head[u] = tol++;
edge[tol].to = u;
edge[tol].cap = 0;
edge[tol].cost = -cost;
edge[tol].flow = 0;
edge[tol].next = head[v];
head[v] = tol++;
}
bool spfa(int s,int t)
{
queue<int>q;
for(int i = 0;i < N;i++)
{
dis[i] = INF;
vis[i] = false;
pre[i] = -1;
}
dis[s] = 0;
vis[s] = true;
q.push(s);
while(!q.empty())
{
int u = q.front();
q.pop();
vis[u] = false;
for(int i = head[u]; i != -1;i = edge[i].next)
{
int v = edge[i].to;
if(edge[i].cap > edge[i].flow &&
dis[v] > dis[u] + edge[i].cost )
{
dis[v] = dis[u] + edge[i].cost;
pre[v] = i;
if(!vis[v])
{
vis[v] = true;
q.push(v);
}
}
}
}
if(pre[t] == -1)return false;
return true;
}
//返回的是最大流，cost存的是最小费用
ll minCostMaxflow(int s,int t)
{
int flow = 0;
ll cost = 0;
while(spfa(s,t))
{
int Min = INF;
for(int i = pre[t];i != -1;i = pre[edge[i^1].to])
{
if(Min > edge[i].cap - edge[i].flow)
Min = edge[i].cap - edge[i].flow;
}
for(int i = pre[t];i != -1;i = pre[edge[i^1].to])
{
edge[i].flow += Min;
edge[i^1].flow -= Min;
cost +=(ll)edge[i].cost * Min;
}
flow += Min;
}
return cost;
}
struct node{
int start,end,cost;
}e[MAXM];
int main(){
int t,n,m;
scanf("%d",&t);
while(t--){
scanf("%d%d",&n,&m);
init(2*m+3);
for(int i=1;i<=m;i++)
scanf("%d%d%d",&e[i].start,&e[i].end,&e[i].cost);
addedge(0,2*m+1,n,0);
for(int i=1;i<=m;i++){
addedge(i,i+m,1,-e[i].cost);
addedge(2*m+1,i,INF,0);
addedge(i+m,2*m+2,INF,0);
}
for(int i=1;i<=m;i++)
for(int j=1;j<=m;j++){
if(e[j].start>e[i].end)
addedge(i+m,j,INF,0);
}
printf("%lld\n",-minCostMaxflow(0,2*m+2));
}
return 0;
}