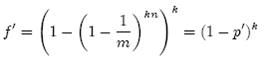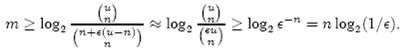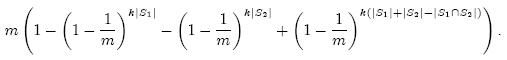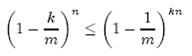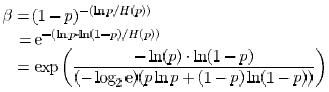Bloom filter

数学之美系列二十一 － 布隆过滤器（Bloom Filter）

2007年7月3日 上午 09:35:00

发表者：Google（谷歌）研究员 吴军 

在日常生活中，包括在设计计算机软件时，我们经常要判断一个元素是否在一个集合中。比如在字处理软件中，需要检查一个英语单词是否拼写正确（也就是要判断它是否在已知的字典中）；在 FBI，一个嫌疑人的名字是否已经在嫌疑名单上；在网络爬虫里，一个网址是否被访问过等等。最直接的方法就是将集合中全部的元素存在计算机中，遇到一个新元素时，将它和集合中的元素直接比较即可。一般来讲，计算机中的集合是用哈希表（hash table）来存储的。它的好处是快速准确，缺点是费存储空间。当集合比较小时，这个问题不显著，但是当集合巨大时，哈希表存储效率低的问题就显现出来了。比如说，一个象 Yahoo,Hotmail 和 Gmai 那样的公众电子邮件（email）提供商，总是需要过滤来自发送垃圾邮件的人（spamer）的垃圾邮件。一个办法就是记录下那些发垃圾邮件的 email 地址。由于那些发送者不停地在注册新的地址，全世界少说也有几十亿个发垃圾邮件的地址，将他们都存起来则需要大量的网络服务器。如果用哈希表，每存储一亿个 email 地址， 就需要 1.6GB 的内存（用哈希表实现的具体办法是将每一个 email 地址对应成一个八字节的信息指纹  googlechinablog.com/2006/08/blog-post.html，然后将这些信息指纹存入哈希表，由于哈希表的存储效率一般只有 50%，因此一个 email 地址需要占用十六个字节。一亿个地址大约要 1.6GB， 即十六亿字节的内存）。因此存贮几十亿个邮件地址可能需要上百 GB 的内存。除非是超级计算机，一般服务器是无法存储的。

今天，我们介绍一种称作布隆过滤器的数学工具，它只需要哈希表 1/8 到 1/4 的大小就能解决同样的问题。

布隆过滤器是由巴顿.布隆于一九七零年提出的。它实际上是一个很长的二进制向量和一系列随机映射函数。我们通过上面的例子来说明起工作原理。

假定我们存储一亿个电子邮件地址，我们先建立一个十六亿二进制（比特），即两亿字节的向量，然后将这十六亿个二进制全部设置为零。对于每一个电子邮件地址 X，我们用八个不同的随机数产生器（F1,F2, ...,F8） 产生八个信息指纹（f1, f2, ..., f8）。再用一个随机数产生器 G 把这八个信息指纹映射到 1 到十六亿中的八个自然数 g1, g2, ...,g8。现在我们把这八个位置的二进制全部设置为一。当我们对这一亿个 email 地址都进行这样的处理后。一个针对这些 email 地址的布隆过滤器就建成了。（见下图）



现在，让我们看看如何用布隆过滤器来检测一个可疑的电子邮件地址 Y 是否在黑名单中。我们用相同的八个随机数产生器（F1, F2, ..., F8）对这个地址产生八个信息指纹 s1,s2,...,s8，然后将这八个指纹对应到布隆过滤器的八个二进制位，分别是 t1,t2,...,t8。如果 Y 在黑名单中，显然，t1,t2,..,t8 对应的八个二进制一定是一。这样在遇到任何在黑名单中的电子邮件地址，我们都能准确地发现。

布隆过滤器决不会漏掉任何一个在黑名单中的可疑地址。但是，它有一条不足之处。也就是它有极小的可能将一个不在黑名单中的电子邮件地址判定为在黑名单中，因为有可能某个好的邮件地址正巧对应个八个都被设置成一的二进制位。好在这种可能性很小。我们把它称为误识概率。在上面的例子中，误识概率在万分之一以下。 

布隆过滤器的好处在于快速，省空间。但是有一定的误识别率。常见的补救办法是在建立一个小的白名单，存储那些可能别误判的邮件地址。

详细的概念介绍：看维基百科http://en.wikipedia.org/wiki/Bloom_filter

 

Bloom Filter概念和原理

分类：  Bloom Filter2007-01-27 12:47  68030人阅读  评论(51)  收藏  举报

目录(?)[+]

Bloom Filter概念和原理

焦萌 2007年1月27日

 

Bloom Filter是一种空间效率很高的随机数据结构，它利用位数组很简洁地表示一个集合，并能判断一个元素是否属于这个集合。Bloom Filter的这种高效是有一定代价的：在判断一个元素是否属于某个集合时，有可能会把不属于这个集合的元素误认为属于这个集合（false positive）。因此，Bloom Filter不适合那些“零错误”的应用场合。而在能容忍低错误率的应用场合下，Bloom Filter通过极少的错误换取了存储空间的极大节省。

集合表示和元素查询

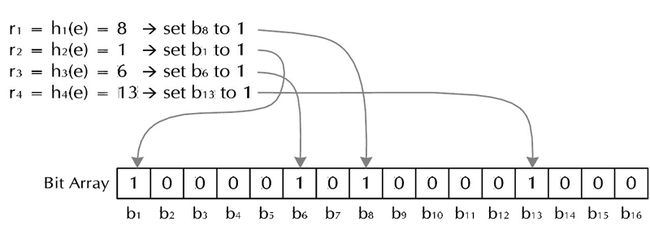
下面我们具体来看Bloom Filter是如何用位数组表示集合的。初始状态时，Bloom Filter是一个包含m位的位数组，每一位都置为0。

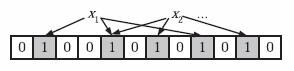
为了表达S={x₁, x₂,…,x_n}这样一个n个元素的集合，Bloom Filter使用k个相互独立的哈希函数（Hash Function），它们分别将集合中的每个元素映射到{1,…,m}的范围中。对任意一个元素x，第i个哈希函数映射的位置h_i(x)就会被置为1（1≤i≤k）。注意，如果一个位置多次被置为1，那么只有第一次会起作用，后面几次将没有任何效果。在下图中，k=3，且有两个哈希函数选中同一个位置（从左边数第五位）。   

 

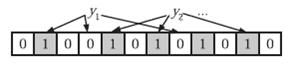
在判断y是否属于这个集合时，我们对y应用k次哈希函数，如果所有h_i(y)的位置都是1（1≤i≤k），那么我们就认为y是集合中的元素，否则就认为y不是集合中的元素。下图中y₁就不是集合中的元素。y₂或者属于这个集合，或者刚好是一个false positive。

错误率估计

前面我们已经提到了，Bloom Filter在判断一个元素是否属于它表示的集合时会有一定的错误率（false positive rate），下面我们就来估计错误率的大小。在估计之前为了简化模型，我们假设kn<m且各个哈希函数是完全随机的。当集合S={x₁, x₂,…,x_n}的所有元素都被k个哈希函数映射到m位的位数组中时，这个位数组中某一位还是0的概率是：

其中1/m表示任意一个哈希函数选中这一位的概率（前提是哈希函数是完全随机的），(1-1/m)表示哈希一次没有选中这一位的概率。要把S完全映射到位数组中，需要做kn次哈希。某一位还是0意味着kn次哈希都没有选中它，因此这个概率就是（1-1/m）的kn次方。令p = e^-kn/m是为了简化运算，这里用到了计算e时常用的近似：

 

令ρ为位数组中0的比例，则ρ的数学期望E(ρ)= p’。在ρ已知的情况下，要求的错误率（false positive rate）为：

(1-ρ)为位数组中1的比例，(1-ρ)^k就表示k次哈希都刚好选中1的区域，即false positive rate。上式中第二步近似在前面已经提到了，现在来看第一步近似。p’只是ρ的数学期望，在实际中ρ的值有可能偏离它的数学期望值。M. Mitzenmacher已经证明^[2] ，位数组中0的比例非常集中地分布在它的数学期望值的附近。因此，第一步的近似得以成立。分别将p和p’代入上式中，得：

   

   

相比p’和f’，使用p和f通常在分析中更为方便。

最优的哈希函数个数

既然Bloom Filter要靠多个哈希函数将集合映射到位数组中，那么应该选择几个哈希函数才能使元素查询时的错误率降到最低呢？这里有两个互斥的理由：如果哈希函数的个数多，那么在对一个不属于集合的元素进行查询时得到0的概率就大；但另一方面，如果哈希函数的个数少，那么位数组中的0就多。为了得到最优的哈希函数个数，我们需要根据上一小节中的错误率公式进行计算。

 

先用p和f进行计算。注意到f = exp(k ln(1 − e^−kn/m))，我们令g = k ln(1 − e^−kn/m)，只要让g取到最小，f自然也取到最小。由于p = e^-kn/m，我们可以将g写成

根据对称性法则可以很容易看出当p = 1/2，也就是k = ln2· (m/n)时，g取得最小值。在这种情况下，最小错误率f等于(1/2)^k ≈ (0.6185)^m/n。另外，注意到p是位数组中某一位仍是0的概率，所以p = 1/2对应着位数组中0和1各一半。换句话说，要想保持错误率低，最好让位数组有一半还空着。

 

需要强调的一点是，p = 1/2时错误率最小这个结果并不依赖于近似值p和f。同样对于f’ = exp(k ln(1 − (1 − 1/m)^kn))，g’ = k ln(1 − (1 − 1/m)^kn)，p’ = (1 − 1/m)^kn，我们可以将g’写成

同样根据对称性法则可以得到当p’ = 1/2时，g’取得最小值。

位数组的大小

下面我们来看看，在不超过一定错误率的情况下，Bloom Filter至少需要多少位才能表示全集中任意n个元素的集合。假设全集中共有u个元素，允许的最大错误率为є，下面我们来求位数组的位数m。

 

假设X为全集中任取n个元素的集合，F(X)是表示X的位数组。那么对于集合X中任意一个元素x，在s = F(X)中查询x都能得到肯定的结果，即s能够接受x。显然，由于Bloom Filter引入了错误，s能够接受的不仅仅是X中的元素，它还能够є (u - n)个false positive。因此，对于一个确定的位数组来说，它能够接受总共n + є (u - n)个元素。在n + є (u - n)个元素中，s真正表示的只有其中n个，所以一个确定的位数组可以表示

个集合。m位的位数组共有2^m个不同的组合，进而可以推出，m位的位数组可以表示

   

个集合。全集中n个元素的集合总共有

   

个，因此要让m位的位数组能够表示所有n个元素的集合，必须有

   

即：

   

上式中的近似前提是n和єu相比很小，这也是实际情况中常常发生的。根据上式，我们得出结论：在错误率不大于є的情况下，m至少要等于n log₂(1/є)才能表示任意n个元素的集合。

 

上一小节中我们曾算出当k = ln2· (m/n)时错误率f最小，这时f = (1/2)^k = (1/2)^{mln2 / n}。现在令f≤є，可以推出

这个结果比前面我们算得的下界n log₂(1/є)大了log₂ e ≈ 1.44倍。这说明在哈希函数的个数取到最优时，要让错误率不超过є，m至少需要取到最小值的1.44倍。

总结

在计算机科学中，我们常常会碰到时间换空间或者空间换时间的情况，即为了达到某一个方面的最优而牺牲另一个方面。Bloom Filter在时间空间这两个因素之外又引入了另一个因素：错误率。在使用Bloom Filter判断一个元素是否属于某个集合时，会有一定的错误率。也就是说，有可能把不属于这个集合的元素误认为属于这个集合（False Positive），但不会把属于这个集合的元素误认为不属于这个集合（False Negative）。在增加了错误率这个因素之后，Bloom Filter通过允许少量的错误来节省大量的存储空间。

 

自从Burton Bloom在70年代提出Bloom Filter之后，Bloom Filter就被广泛用于拼写检查和数据库系统中。近一二十年，伴随着网络的普及和发展，Bloom Filter在网络领域获得了新生，各种Bloom Filter变种和新的应用不断出现。可以预见，随着网络应用的不断深入，新的变种和应用将会继续出现，Bloom Filter必将获得更大的发展。

参考资料

[1] A. Broder and M. Mitzenmacher. Network applications of bloom filters: A survey. Internet Mathematics, 1(4):485–509, 2005.

[2] M. Mitzenmacher. Compressed Bloom Filters. IEEE/ACM Transactions on Networking 10:5 (2002), 604—612.

[3] www.cs.jhu.edu/~fabian/courses/CS600.624/slides/bloomslides.pdf

[4] http://166.111.248.20/seminar/2006_11_23/hash_2_yaxuan.ppt

BloomFilter——大规模数据处理利器

 

　　Bloom Filter是由Bloom在1970年提出的一种多哈希函数映射的快速查找算法。通常应用在一些需要快速判断某个元素是否属于集合，但是并不严格要求100%正确的场合。

 

一. 实例 

　　为了说明Bloom Filter存在的重要意义，举一个实例：

　　假设要你写一个网络蜘蛛（web crawler）。由于网络间的链接错综复杂，蜘蛛在网络间爬行很可能会形成“环”。为了避免形成“环”，就需要知道蜘蛛已经访问过那些URL。给一个URL，怎样知道蜘蛛是否已经访问过呢？稍微想想，就会有如下几种方案：

　　1. 将访问过的URL保存到数据库。

　　2. 用HashSet将访问过的URL保存起来。那只需接近O(1)的代价就可以查到一个URL是否被访问过了。

　　3. URL经过MD5或SHA-1等单向哈希后再保存到HashSet或数据库。

　　4. Bit-Map方法。建立一个BitSet，将每个URL经过一个哈希函数映射到某一位。

　　方法1~3都是将访问过的URL完整保存，方法4则只标记URL的一个映射位。

 

　　以上方法在数据量较小的情况下都能完美解决问题，但是当数据量变得非常庞大时问题就来了。

　　方法1的缺点：数据量变得非常庞大后关系型数据库查询的效率会变得很低。而且每来一个URL就启动一次数据库查询是不是太小题大做了？

　　方法2的缺点：太消耗内存。随着URL的增多，占用的内存会越来越多。就算只有1亿个URL，每个URL只算50个字符，就需要5GB内存。

　　方法3：由于字符串经过MD5处理后的信息摘要长度只有128Bit，SHA-1处理后也只有160Bit，因此方法3比方法2节省了好几倍的内存。

　　方法4消耗内存是相对较少的，但缺点是单一哈希函数发生冲突的概率太高。还记得数据结构课上学过的Hash表冲突的各种解决方法么？若要降低冲突发生的概率到1%，就要将BitSet的长度设置为URL个数的100倍。

 

　　实质上上面的算法都忽略了一个重要的隐含条件：允许小概率的出错，不一定要100%准确！也就是说少量url实际上没有没网络蜘蛛访问，而将它们错判为已访问的代价是很小的——大不了少抓几个网页呗。 

 

二. Bloom Filter的算法 

 

　　废话说到这里，下面引入本篇的主角——Bloom Filter。其实上面方法4的思想已经很接近Bloom Filter了。方法四的致命缺点是冲突概率高，为了降低冲突的概念，Bloom Filter使用了多个哈希函数，而不是一个。

   　Bloom Filter算法如下：

  　 创建一个m位BitSet，先将所有位初始化为0，然后选择k个不同的哈希函数。第i个哈希函数对字符串str哈希的结果记为h（i，str），且h（i，str）的范围是0到m-1 。

 

(1) 加入字符串过程 

 

　　下面是每个字符串处理的过程，首先是将字符串str“记录”到BitSet中的过程：

　　对于字符串str，分别计算h（1，str），h（2，str）…… h（k，str）。然后将BitSet的第h（1，str）、h（2，str）…… h（k，str）位设为1。

 

　　图1.Bloom Filter加入字符串过程

　　很简单吧？这样就将字符串str映射到BitSet中的k个二进制位了。

 

(2) 检查字符串是否存在的过程 

 

　　下面是检查字符串str是否被BitSet记录过的过程：

　　对于字符串str，分别计算h（1，str），h（2，str）…… h（k，str）。然后检查BitSet的第h（1，str）、h（2，str）…… h（k，str）位是否为1，若其中任何一位不为1则可以判定str一定没有被记录过。若全部位都是1，则“认为”字符串str存在。

 

　　若一个字符串对应的Bit不全为1，则可以肯定该字符串一定没有被Bloom Filter记录过。（这是显然的，因为字符串被记录过，其对应的二进制位肯定全部被设为1了）

　　但是若一个字符串对应的Bit全为1，实际上是不能100%的肯定该字符串被Bloom Filter记录过的。（因为有可能该字符串的所有位都刚好是被其他字符串所对应）这种将该字符串划分错的情况，称为false positive 。

 

(3) 删除字符串过程 

   字符串加入了就被不能删除了，因为删除会影响到其他字符串。实在需要删除字符串的可以使用Counting bloomfilter(CBF)，这是一种基本Bloom Filter的变体，CBF将基本Bloom Filter每一个Bit改为一个计数器，这样就可以实现删除字符串的功能了。

 

　　Bloom Filter跟单哈希函数Bit-Map不同之处在于：Bloom Filter使用了k个哈希函数，每个字符串跟k个bit对应。从而降低了冲突的概率。

 

三. Bloom Filter参数选择 

 

   (1)哈希函数选择

   　　哈希函数的选择对性能的影响应该是很大的，一个好的哈希函数要能近似等概率的将字符串映射到各个Bit。选择k个不同的哈希函数比较麻烦，一种简单的方法是选择一个哈希函数，然后送入k个不同的参数。

   (2)Bit数组大小选择 

   　　哈希函数个数k、位数组大小m、加入的字符串数量n的关系可以参考参考文献1。该文献证明了对于给定的m、n，当 k = ln(2)* m/n 时出错的概率是最小的。

   　　同时该文献还给出特定的k，m，n的出错概率。例如：根据参考文献1，哈希函数个数k取10，位数组大小m设为字符串个数n的20倍时，false positive发生的概率是0.0000889 ，这个概率基本能满足网络爬虫的需求了。  

 

四. Bloom Filter实现代码 

  　 下面给出一个简单的Bloom Filter的Java实现代码：

 

import java.util.BitSet;

publicclass BloomFilter 
{
/* BitSet初始分配2^24个bit */ 
privatestaticfinalint DEFAULT_SIZE =1<<25; 
/* 不同哈希函数的种子，一般应取质数 */
privatestaticfinalint[] seeds =newint[] { 5, 7, 11, 13, 31, 37, 61 };
private BitSet bits =new BitSet(DEFAULT_SIZE);
/* 哈希函数对象 */ 
private SimpleHash[] func =new SimpleHash[seeds.length];

public BloomFilter() 
{
for (int i =0; i < seeds.length; i++)
{
func[i] =new SimpleHash(DEFAULT_SIZE, seeds[i]);
}
}

// 将字符串标记到bits中
publicvoid add(String value) 
{
for (SimpleHash f : func) 
{
bits.set(f.hash(value), true);
}
}

//判断字符串是否已经被bits标记
publicboolean contains(String value) 
{
if (value ==null) 
{
returnfalse;
}
boolean ret =true;
for (SimpleHash f : func) 
{
ret = ret && bits.get(f.hash(value));
}
return ret;
}

/* 哈希函数类 */
publicstaticclass SimpleHash 
{
privateint cap;
privateint seed;

public SimpleHash(int cap, int seed) 
{
this.cap = cap;
this.seed = seed;
}

//hash函数，采用简单的加权和hash
publicint hash(String value) 
{
int result =0;
int len = value.length();
for (int i =0; i < len; i++) 
{
result = seed * result + value.charAt(i);
}
return (cap -1) & result;
}
}
}

 

 

 

参考文献：

 

[1]Pei Cao. Bloom Filters - the math.

http://pages.cs.wisc.edu/~cao/papers/summary-cache/node8.html

[2]Wikipedia. Bloom filter.

http://en.wikipedia.org/wiki/Bloom_filter

分类:  数据结构·算法

 

 

应用Bloom Filter的几个小技巧

分类：  Bloom Filter2007-01-29 19:32  3839人阅读  评论(0)  收藏  举报

应用Bloom Filter的几个小技巧

焦萌 2007年1月29日

 

下面列举几个基于标准Bloom Filter的小技巧：

 

1.         求两个集合的并。假设有两个Bloom Filter分别表示集合S₁和S₂，它们位数组的大小相同且使用同一组哈希函数，那么要求表示S₁和S₂并集的Bloom Filter，只要将S₁和S₂的位数组进行“或”操作即可得到结果。

 

2.         将Bloom Filter“对折”。 如果想将一个Bloom Filter的大小缩小一半，那么只需将Bloom Filter的位数组分成两半进行“或”操作，得到的结果即为所求。在查找某一元素时，需要将哈希后的索引地址的最高位屏蔽掉。

 

3.         通过0的数目估计集合元素个数。在第一篇文章Bloom Filter概念和原理中，我们提到过：位数组中0的比例非常集中地分布在它的数学期望值m (1 - 1/m)^kn的附近，其中m为位数组的大小，k为哈希函数的个数，n为Bloom Filter所表示集合的元素个数。根据上式，知道了0的个数就可以很容易推断n的大小。

 

4.         通过内积估计集合交集元素个数。假设有两个Bloom Filter分别表示集合S₁和S₂，它们位数组的大小相同且使用同一组哈希函数，下面我们来看第i位在两个Bloom Filter同时被置为1的概率。要让某一位同时被置为1，只有两种可能：要么它是被S₁∩S₂中的元素设置的，要么分别是被S₁ – (S₁∩S₂)和S₂ - (S₁∩S₂)中的元素设置的。因此第i位在两个Bloom Filter同时被置为1的概率为：

|S|表示S中元素的个数，k表示哈希函数的个数，m表示位数组的大小。经过化简，再乘以m，得到两个位数组内积的数学期望值为：

如果不知道|S₁|和|S₂|，可以用3中的方法根据0的个数估计出它们的大小。最后，根据上式，我们在知道内积的情况下就可以很容易推断| S₁∩S₂|的大小。

 

5.         表示全集。很简单，将位数组设为全1就可以表示全集了，因为查找任何一个元素都会得到肯定的结果。

 

 

Counting Bloom Filter

分类：  Bloom Filter2007-01-30 22:25  5340人阅读  评论(3)  收藏  举报

Counting Bloom Filter

焦萌 2007年1月30日

 

从前面几篇对Bloom Filter的介绍可以看出，标准的Bloom Filter是一种很简单的数据结构，它只支持插入和查找两种操作。在所要表达的集合是静态集合的时候，标准Bloom Filter可以很好地工作，但是如果要表达的集合经常变动，标准Bloom Filter的弊端就显现出来了，因为它不支持删除操作。

 

Counting Bloom Filter的出现解决了这个问题，它将标准Bloom Filter位数组的每一位扩展为一个小的计数器（Counter），在插入元素时给对应的k（k为哈希函数个数）个Counter的值分别加1，删除元素时给对应的k个Counter的值分别减1。Counting Bloom Filter通过多占用几倍的存储空间的代价，给Bloom Filter增加了删除操作。下一个问题自然就是，到底要多占用几倍呢？

 

 

我们先计算第i个Counter被增加j次的概率，其中n为集合元素个数，k为哈希函数个数，m为Counter个数（对应着原来位数组的大小）：

上面等式右端的表达式中，前一部分表示从nk次哈希中选择j次，中间部分表示j次哈希都选中了第i个Counter，后一部分表示其它nk – j次哈希都没有选中第i个Counter。因此，第i个Counter的值大于j的概率可以限定为：

上式第二步缩放中应用了估计阶乘的斯特林公式：

在Bloom Filter概念和原理一文中，我们提到过k的最优值为(ln2)m/n，现在我们限制k ≤ (ln2)m/n，就可以得到如下结论：

如果每个Counter分配4位，那么当Counter的值达到16时就会溢出。这个概率为：

这个值足够小，因此对于大多数应用程序来说，4位就足够了。

 

 关于Counting Bloom Filter最早的论文：Summary Cache: A Scalable Wide-Area Web Cache Sharing Protocol

 

 

Partial Bloom Filter

焦萌 2007年2月5日

 

在标准的Bloom Filter中，我们用k个相互独立的哈希函数将一个集合映射到长度为m的位数组中，其中每个哈希函数的映射范围都为{0, … , m-1}。除了这种标准的实现方式之外，还有一种实现被广泛采用，就是所谓的Partial Bloom Filter。

 

Partial Bloom Filter和标准Bloom Filter唯一不同的地方在于哈希函数的映射范围。在Partial Bloom Filter中，位数组被等分成k个区域，每个哈希函数只映射到其中一个区域。也就是说，每个哈希函数映射范围都是{0, … , m/k - 1}，但互不重叠，大家各自负责各自的区域。

 

下面我们来估算一下这种实现的错误率。位数组中某一位只可能被一个哈希函数选中，且选中的概率为k/m，所以这一位不被选中的概率为1 – k/m。假设集合有n个元素，那么这一位在存储完整个集合后还保持为0的概率为(1 – k/m)ⁿ。由于(1 – k/m)ⁿ ≈ e^-kn/m，所以Partial Bloom Filter和标准Bloom Filter的错误率很近似。如果一定要分出个高下，实际上标准Bloom Filter错误率要小一些，因为对于k≥1，有

 

在实际应用中，Partial Bloom Filter有一定的优势，因为一旦哈希函数的映射范围也独立开来，k个哈希函数就可以并行访问位数组，从而提高程序性能。

 

 

 

2007-02-08 14:10  2350人阅读  评论(0)  收藏  举报

Compressed Bloom Filter

焦萌 2007年2月8日

 

在前面的讨论中，我们都只将Bloom Filter作为一种表示集合的数据结构。但在网络应用中，Bloom Filter经常被当作节点之间交换信息时传递的消息。从这个角度考虑，我们自然希望消息在传递之前能够被压缩。

 

那么Bloom Filter到底能不能被压缩？在Bloom Filter概念和原理一文中，我们知道当Bloom Filter的错误率最低时，位数组中任意一位是0的概率p = 1/2。也就是说，在错误率最低时位数组中0和1的概率各占一半。根据Claude Shannon 编码原理，位数组将不可能获得任何压缩的效果。

 

然而事实并不是这样，因为p = 1/2的结论是这样作出的：在已知位数组大小m和集合元素个数n的情况下，我们求出最优的哈希函数个数k，使得错误率降到最低。这样求出的k = (m/n) ln2，位数组中任意一位是0的概率p = 1/2。这个分析思路没有考虑压缩，而是把Bloom Filter作为一种内存中的数据结构，在分配的位数组大小固定的情况下求哈希函数个数的最优值。

 

从上面的分析可以看出，在不考虑压缩的情况下，Bloom Filter有三个重要的性能参数：错误率f、哈希函数个数k和位数组大小m。在引入压缩之后，性能参数变成了四个：错误率f、哈希函数个数k、未压缩的位数组大小m和压缩后的位数组大小z。在多了一个因素之后，整个分析的思路会大不一样，因此不能简单地延续前面的结论继续分析。

 

下面我们就分析一下引入压缩之后，如何选择各个性能参数以达到最优的结果。在不考虑压缩的情况下，我们考虑的问题是：给定m和n，求最优的k，使得f最小。在考虑压缩的情况下，压缩后的位数组大小z比压缩前的大小m更重要，因为它是我们实际在网络上传输的消息大小。基于这个原因，我们考虑的问题就变成了：给定z和n，求最优的k和m，使得f最小。

 

首先假设我们有一个最优的压缩算法，使得z = m H(p)，其中H(p) = -plog₂p – (1-p)log₂(1-p)是信息熵函数（p是位数组某一位为0的概率）。在Bloom Filter概念和原理一文中，我们知道p ≈ e^-kn/m，从而有k ≈ (-lnp) (m/n)。于是错误率f就可以写成p的函数

f = (1 - p)^k = (1 - p)^{(-lnp) (m/n)}

再将m = z / H(p)带入上式，可得

f = (1 - p)^{-(zlnp/nH(p))}

由于z和n固定，且z ≥ n，要求f的最小值，即求β = f^n/z的最小值。将H(p) = -plog₂p – (1-p)log₂(1-p)代入可得

要求β的最小值，即求指数的最小值，也等于求

的最大值。对上式求导，得

令dγ/dp = 0，得p = 1/2。并且可以发现当p < 1/2时dγ/dp小于0，当p > 1/2时dγ/dp大于0。因此当p = 1/2时γ取得最小值，即β和f取得最大值。这个结论非常有意思：当p = 1/2，即k = (ln2) (m/n)时，在不考虑压缩的情况下错误率最低，而在考虑压缩的情况下错误率反而最高。换句话说，压缩总是能够降低错误率。

 

由于压缩总能降低错误率，因此对比标准的Bloom Filter，Compressed Bloom Filter性能更加出色。而且由于Compressed Bloom Filter增加了一个性能参数，它在各个性能参数的权衡上更加灵活。例如，用同样的位数表示集合元素，Compressed Bloom Filter的错误率更低，所用的哈希函数个数更少：

上表中的第一列就是标准的Bloom Filter，没有压缩（m/n = z/n），每一个元素用8位表示。后两列是经过压缩的Bloom Filter，同样每一个元素用接近8位表示，但用的哈希函数个数更少，错误率更低。又例如，达到同样的错误率，Compressed Bloom Filter每一个元素所占位数更少，哈希函数个数也更少：

 

总之，在网络应用环境下，按( m/ n) ln2选择最优k 值不会获得任何的传输压缩率。相反，若增大本地节点表示信息的位数和选择较小的k值，不仅可以获得好的传输压缩率同时还能获得更小的错误率。

 

参考论文：Compressed Bloom Filters