数据结构与算法13: B-Tree
写在前面
B树用于操作辅助存储器,经常用作数据库的索引,是一种很有用的数据结构。本节,主要总结B-Tree的基本概念,实现B-Tree的操作。关于为什么需要B-Tree以及它在数据库中作用,可以参看文章:MySQL索引背后的数据结构及算法原理。
1. 定义
B-Tree: m阶的B树具有下列特性的多叉搜索树:
(1) 根节点至少有两个子树,除非它是一个叶节点
(2) 每个非根非叶节点都有k-1个键值和k个指向子树的指针
其中键的数目k-1的上下界为:[ ⌈m/2⌉−1,m−1 ] ,例如5阶的B-Tree,键数目为[2,4]。
(3) 每个叶节点都含有k-1个键值,k-1需要满足上下界要求
(4) 所有的叶节点在同一层
B-Tree的阶,可以理解为孩子节点的最大数目。
B-Tree的节点可以定义为:
template <class T, int M>
class BTreeNode
{
public:
BTreeNode();
BTreeNode( const T & );
private:
T keys[M-1];
BTreeNode *pointers[M];
...
};在实现的过程中,为了方便,我们将节点定义为:
/** * M阶B-Tree结点 * 每个节点包含M-1个键值和M个指针 * 实际上每个结点多分配一个键值和指针用于辅助空间 */
template<typename T,int M> class BTree;
template<typename T,int M=5>
class BTreeNode {
public:
BTreeNode():parent(0),keynum(0),isLeaf(true) {
for(int i=0;i < M+1;++i)
childs[i] = 0;
}
BTreeNode(const T& k,BTreeNode *p=0) {
keys[0]=k;
parent = p;
keynum = 1;
isLeaf = true;
for(int i=0;i < M+1;++i)
childs[i] = 0;
}
private:
T keys[M]; // 键
BTreeNode *childs[M+1]; // 孩子指针
BTreeNode *parent; // 父节点指针
int keynum; // 键数目
bool isLeaf; // 是否是叶子结点
friend class BTree<T,M>;
friend class BTreePrinter;// 打印B-Tree为图片
};这里为每个节点多分配一个键值和指针的空间,主要是为了在插入的过程中,插入后如果键值超过上限则分裂,我们使用先插入后分裂的策略,因此需要多出一个空间用于辅助算法。当然,如果能不使用这个多余的空间,预先判定是否需要分裂,然后再插入的话,空间利用更合理,但是算法实现将变得困难,本节主要是熟悉B-tree的基本内容,因此我们使用这个多出的辅助空间完成操作。编写一个高效的B-Tree是一个有挑战性的工作,你可以参考google B-Tree 的代码。
2. 查找操作
给出下面的B-Tree:
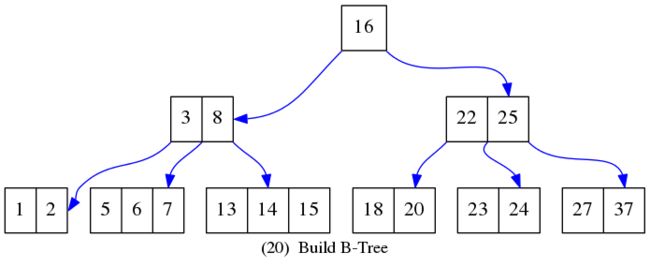
查找15的过程为:
首先,在节点16中比较,确定比16小,则在第一个孩子节点中比较;确定比8大,则在右边孩子中比较;与13,14,15比较后,最终找到键值15的位置。
算法的思想就是:
(1)在当前节点中,找第一个键大于等于键值的位置pos。
(2)如果位置pos没有超出末端且值等于查找值,则找到返回true;
否则,如果当前节点的pos位置孩子节点不为空,则将其设为当前节点,重复1,继续查找;否则返回false
算法实现为:
/** * 搜索键e * 如果找到包含e的结点,则返回包含e的结点 * 否则返回0 */
template<typename T,int M>
BTreeNode<T,M> * BTree<T,M>::search(const T&e) {
BTreeNode<T,M>* p = 0;
int pos = -1;
bool ret = search(e,p,pos);
if(ret)
return p;
else
return 0;
}用于搜索的两个辅助函数为:
/** * 搜索键值e * 搜索成功返回true,失败返回false * 搜索成功时node返回包含键值的节点和位置 * 搜索失败时返回e应该插入的节点和位置 */
template<typename T,int M>
bool BTree<T,M>::search(const T&e,BTreeNode<T,M> *&node,int &pos) {
node = root;
bool found = false;
while( node != 0 && !found) {
pos = searchInNode(node,e);
if(node->keys[pos] == e ) // 找到
found = true;
else if(node->childs[pos] != 0) // 继续找
node = node->childs[pos];
else
break; // 未找到
}
return found;
}
/** * 在结点node中搜索键值k * 返回第一个大于等于k的索引 * 如果不存在大于等于k的索引则返回node结点的数目 */
template<typename T,int M>
int BTree<T,M>::searchInNode(BTreeNode<T,M> *node,const T&k) {
int i = 0;
for(; i < node->keynum && node->keys[i] < k;++i);
return i;
}3. 插入操作-注意键数上溢情况
插入过程必须维护B-Tree定义表达的约束,即插入时如果节点键数目超过上限,则必须将其分裂,分裂的中间值插入到父节点,依次类推。
插入键k的过程有三种情况,要处理:
(1) case 1: 插入的节点p尚有空间存放键值即 p->keynum < MAX_KEY_NUM
这时直接插入键k,并且调整节点p的键值为有序状态即可。
例如如下情况(以下case图片均来自:Multiway Trees):
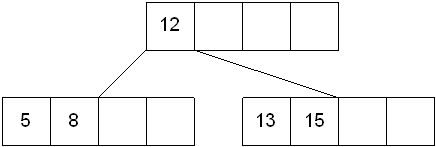
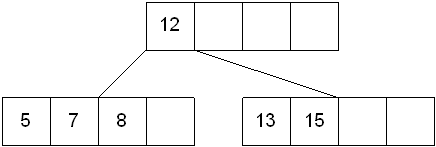
(2) case 2: 插入的节点p键没有多余空间存放,即p->keynum == MAX_KEY_NUM
这时需要将插入节点分裂为两个节点,并且将划分这两个节点的中间值插入到上层节点中,如下图所示:
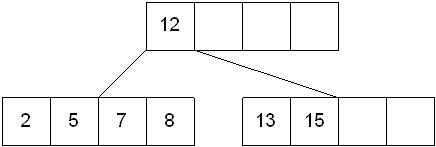
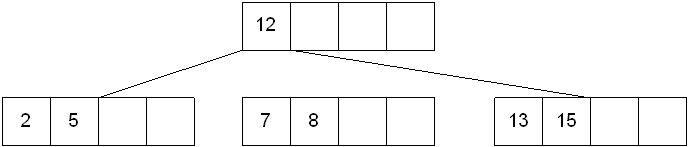
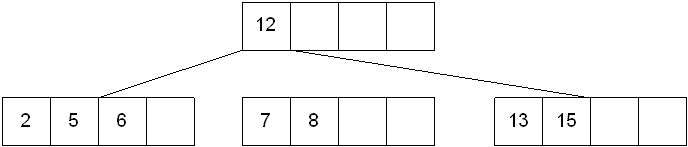
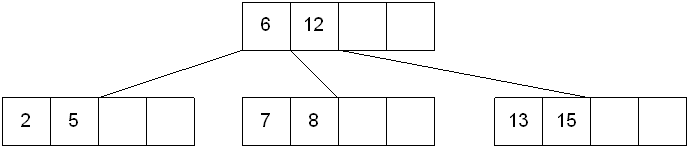
本节,我们采用策略是先插入后分裂的策略,即将6先插入节点[2,5,7,8],然后判断其键值是否超过上限,超过上限则分裂。
(3) case 3: 如果将划分的键值插入到根节点时,根节点已经是满的(即键值数目达到上限)则要分裂根节点,产生新的根节点。这是case2的特殊情形。
算法思想为:
(1) 查找插入节点p和位置pos,划分节点的右孩子sright=0
(2) 在节点p中pos处插入键k和sright
(3) 如果p节点键值未超过上限,则退出;
否则: 分裂p为[左边节点p,中间键k,以及右边节点sright]
如果p是根节点,则将中间键k重建为根,并将p和sright设置其左右孩子,退出;
否则查找k在父节点中位置,继续过程2,3
插入操作的实现:
在实现的过程中,我们需要的辅助操作为:
(1)切分节点 SplitNode操作
(2)切分节点的过程中,将键和孩子指针复制和移动的操作
rightShiftElements,copyElements操作。
辅助函数在文章末尾给出。
算法实现:
/** * 插入键e * 插入成功返回true,已经存在则插入失败返回false * 算法思想: * 1)树为空,则插入e为根节点并返回true,其他情况则继续 * 2)找到要插入的结点node和位置pos,如果已经包含键e则插入失败,返回false * 3)在插入结点node中插入e,并检测插入位置键数量是否上溢(overflow) * 如果没有上溢则返回 * 否则,分解当前节点,并将中间值k和分解的右分支sright,继续插入到父节点中去(为根节点则创建新的根) * 4)重复3的过程直到node结点为根或者不在上溢为止 */
template<typename T,int M>
bool BTree<T,M>::insert(const T&e) {
if(root == 0) {
root = new BTreeNode<T,M>(e,0);
return true;
}
BTreeNode<T,M>* sright=0,* p = root;
int pos = -1;
T k = e;
bool ret = search(e,p,pos);
if(ret)
return false; // 已经存在键e则返回
while(p != 0) {
insert(p,pos,k,sright);
if(p->keynum <= MAX_KEY_NUM)
break;
else { // 插入键k后上溢
splitNode(p,k,sright); // 切分结点p
if(p->parent == 0) { // 重构根节点
root = new BTreeNode<T,M>(k,0);
root->childs[0] = p;
p->parent = root;
root->childs[1] = sright;
sright->parent = root;
root->isLeaf = false;
break;
}else {
p = p->parent;
pos = searchInNode(p,k);
}
}
}
return true;
}在叶子节点插入和在非叶子插入时,我们统一处理为:
insert(p,pos,k,sright);这样是为了简洁代码。在叶子中插入时sright为0。
4.删除操作-注意键数下溢情况
删除键值的时候,要注意键值数目下溢的情况,即删除后一个节点的键数目下限。删除非叶子节点中键值时,使用二叉搜索树的复制删除技术,即寻找待删除键的前驱节点pred(或者使用后继节点,类似操作),将pred键复制到待删除节点中,然后删除pred节点中前驱键值即可,也就是转换为叶子的情况。实际上有一种特殊情形,case 1: 即当只有根节点一个节点时,删除键值,这是根作为叶子节点,删除时当删除完所有键后,需要重设根root为0。
因此主要考虑在叶子中删除,包括:
(1) case 2: 删除节点,键数目 > MIN_KEY_NUM
直接删除,调整键为有序即可。
例如初始如下:
删除键6后如下图所示:
(2) case 3: 删除节点p键数目=MIN_KEY_NUM,同时存在同级兄弟节点sibing键>MIN_KEY_NUM,则将[p,sibling,以及划分p和sibling的中间键k]在p和sibling之间重新分配。
例如上面删除6后的图,继续删除键7得到:

存在同级节点[13,14,15],满足键>MIN_KEY_NUM,则重新分配键值后,如下图所示:

(3) case 4: 删除节点p键数目=MIN_KEY_NUM,同时不存在同级兄弟节点sibing键>MIN_KEY_NUM,此时,合并p和其同级节点sibling以及划分键值k。
例如上述删除7后图,继续删除8,则得到:
合并同级节点[14,15]后如下图所示:
合并的特殊情况是,如果合并节点其父节点是根,且根只有一个键时,合并后,需要重新构建根节点,上述从3“借走”13后,3所在节点也下溢则继续合并或者重新分配键值,此处是合并节点,且3的父节点是根,则合并并重新构建根节点如下图所示:
从非叶子中删除,节点例如上图中,继续删除16,则用其前驱15替换其值,然后删除15即可,如下图所示:
用前驱键值替换16:

删除操作需要特别提醒注意的是:
寻找节点的同级节点时,优先选择左边或者右边键值数目较多的节点,因此同级节点可能是左边的兄弟,也可能是右边的兄弟,不要认为只能是右边的同级节点。
算法思想:
(1)查找删除的节点p和位置pos,如果是非叶子节点,则定位其前驱pred,使用复制删除,转换为删除叶子节点p和位置pos
(2)从叶子p中pos处删除键;如果满足case 1则处理之
(3) 如果p中键数目不小于下限,则按case2处理(即退出)
否则:按case3和case4处理,这一过程可能会重复进行
算法实现为:
/** * 删除键e * 删除成功则返回true,不包含键e则删除失败返回false * 算法思想: * 1)找到要包含键e的节点node,找不到则返回false * 2)case 0 : node是非叶节点,则使用复制删除,node的前驱当做叶子处理 * 删除叶子节点中键e * case 1: node是根节点作为叶子节点删除时,则退出(当根节点键数目为0时,根设为空) * 3)case 2: node键数大于等于下限 则退出 * case 3: node键数等于下限,同级节点键数大于下限,则重新分配键值,退出 * case 4: node键数等于下限,同级节点键数等于下限,则合并键值到node * 如果父节点为根节点,退出(当父节点键值为1个,则重建根节点) * 否则将父节点作为node,重复3 */
template<typename T,int M>
bool BTree<T,M>::remove(const T&e) {
BTreeNode<T,M>* p = 0;
int pos = -1;
bool ret = search(e,p,pos);
if(!ret)
return false;
if(!p->isLeaf) { // case 0 寻找前驱 复制删除
BTreeNode<T,M> * pred = p->childs[pos];
while(pred->childs[pred->keynum] != 0)
pred = pred->childs[pred->keynum];
p->keys[pos] = pred->keys[pred->keynum-1]; // 前驱键值复制到待删除键位置
p = pred;
pos = p->keynum-1;
}
removeInleaf(p,pos); // 叶子中删除
if(p == root) { // case 1 如果根节点作为叶子删除
if(root->keynum == 0) {
delete root;
root = 0;
}
return true;
}
bool bfinished = false;
int curIndex = 0,sibIndex=0;
while(!bfinished) {
if(p->keynum >= MIN_KEY_NUM) // case 2
break;
getProperSibling(p,curIndex,sibIndex); // 获取合适的同级节点
if(p->parent->childs[sibIndex]->keynum > MIN_KEY_NUM) {// case 3
reallocKeys(p->parent,curIndex,sibIndex);
bfinished = true;
}else {
mergeNode(p->parent,curIndex,sibIndex); // case 4
if(p->parent == root) {
bfinished = true;
if(root->keynum == 0) {
delete root;
root = p; // 重建根结点
root->parent = 0;
}
}else
p = p->parent;
}
}
return true;
}其中需要的辅助函数为:
removeInLeaf,getProperSibling,reallocKeys,mergeNode四个函数。
5. 辅助函数
这部分内容根据实现而不同,涉及到过多的细节,列出这些函数来只是为了内容完整,你可以根据你的实现自己决定怎么去做。
作为我实现的一个版本,我举出需要的辅助函数。
B-Tree的基本思想并不复杂,但是在分裂和合并节点的过程中,键和孩子指针的维护却比较困难。因此必须借助辅助函数来完成较大的任务。
其中主要的辅助函数包括:
// 将p划分为两个节点
void splitNode(BTreeNode<T,M>*p, T&k,BTreeNode<T,M>*& sright);
// 从叶子中删除pos处键
void removeInleaf(BTreeNode<T,M>*leaf,int pos);
// 在parent的cur和sib中重新分配键
void reallocKeys(BTreeNode<T,M> *parent, int curIndex, int sibIndex);
// 合并parent的cur和sib到cur
void mergeNode(BTreeNode<T,M>*parent,int curIndex,int sibIndex);
//获取cur的适当同级节点
void getProperSibling(BTreeNode<T,M>*current,int &curIndex, int &sibIndex);
// 复制元素
void copyElements(BTreeNode<T,M> *desp,int desIndex,BTreeNode<T,M>* srcp,int srcIndex);
// 左移元素
void leftShiftElements(BTreeNode<T,M> *p,int index,bool withLeftChild=true);
// 右移元素
void rightShiftElements(BTreeNode<T,M> *p,int index,bool leftEmpty=true,int step=1);其中需要注意的是移动元素的情况。
左移动元素时,同级为右兄弟重分配键值时,需要保留index处左侧指针;合并时调整父节点时,不需要保留左侧指针。
右移动元素时,插入时不需要保留index处左侧指针;同级为左兄弟合并节点时,保留index处左侧指针;同级为左兄弟重分配键值时,需要保留index处左侧指针。
我实现的版本经过5阶和7阶测试,经过随机插入、查找和删除测试,完整代码在:
github B-Tree上。
在实现过程中,要保持较好的性能,需要在划分和合并节点时下功夫,保持这个模块的代价较小。有兴趣的可以自行参考谷歌的实现。