基础树状数组

如果给定一个数组，要你求里面所有数的和，一般都会想到累加。但是当那个数组很大的时候，累加就显得太耗时了，时间复杂度为O(n)，并且采用累加 的方法还有一个局限，那就是，当修改掉数组中的元素后，仍然要你求数组中某段元素的和，就显得麻烦了。树状数组是一个查询和修改复杂度都为log(n)的数据结构。主要用于查询任意两位之间的所有元素之和，但是每次只能修改一个元素的值；经过简单修改可以在log(n)的复杂度下进行范围修改，但是这时只能查询其中一个元素的值。

基本概念：

假设数组a[1..n]，那么查询a[1]+...+a[n]的时间是log级别的，而且是一个在线的数据结构，支持随时修改某个元素的值，复杂度也为log级别。

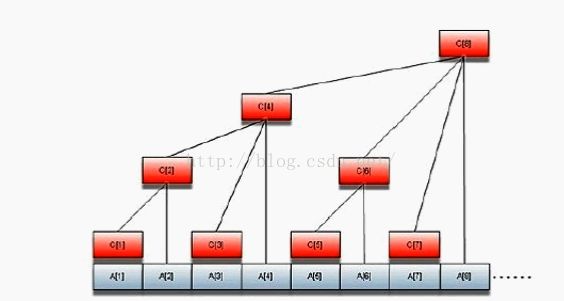
如图所示，c[1]=A[1],c[2]=A[1]+A[2],c[3]=A[3],c[4]=c[2]+c[3]+A[4]=A[1]+A[2]+A[3]+A[4]……；

c[n]=A[n – 2^k + 1]+..…+A[n]；k为n的二进制从右往左数0连续的个数。

计算2^k用下面的方法：

int lowbit(int x)
{
	return x&(x^(x-1));
} 

利用机器补码特性，也可以写成：

int lowbit(int x)
{
	return x&(-x);
} 

x&（-x）是个神奇的方法。

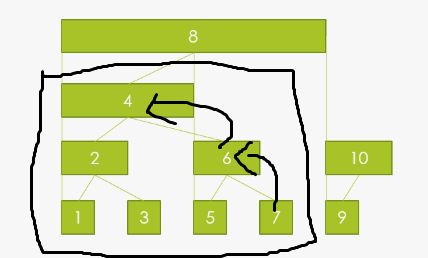
x+=x&(-x)可以找到他的上一个节点，例如x=4，得到8；

x-=x&(-x)就是可以得到x所管辖的下个节点，例如x=7，然后得6，一直循环到x为0，就可以得到7所管辖的区域为1，2，3，4，5，6，7；

void add(int i,int x)
{
	while(i<=n)
	{
		c[i]=c[i]+x;
		i+=loebit(i);
	}
}

上面函数是修改的，因为树状数组是有管辖区域的，所以只要改一个点，那么它所管辖的店都要修改；

int Sum(int n)
{
	sum=0;
	while(n>0)
	{
		sum+=c[n];
		n-=loebit(n);
	}
}

上面是求和函数；

例如：求1到7的和，代入Sum函数，循环一次走到6，再循环一次走到4，然后就循环结束了；

这是树状 数组的基本应用；

大神讲解：

http://blog.csdn.net/int64ago/article/details/7429868

http://www.cnblogs.com/zhangshu/archive/2011/08/16/2141396.html

http://blog.csdn.net/shahdza/article/details/6314818