相似项发现（三）--LSH

四、文档的局部敏感哈希算法（LSH）

即使可以使用最小哈希将大文档压缩成小的签名并同时保持任意对文档之间的预期相似度，但是高效寻找具有最大相似度的文档对仍然是不可能的。主要原因在于，即使文档本身的数目并不是很大，但是需要比较的文档对的数目可能很大。

例如：假定有100万篇文档，每篇文档使用的签名的长度为250，则每篇文档需要250*4 bytes来表示签名。所有100万篇文档的签名数据占用1GB空间。这个数字小于普通台式机的内存大小。然而，有C2 20 即约5000亿个文档对需要比较。如果计算每两篇文档签名之间的相似度需要花费1微秒，那么这台计算机需要大约6天才能计算所有的相似度。

如果我们的目标是计算每对文档的相似度，那么即使采用并行机制来减小实耗时间，也没有办法来减少计算量。但是，实际中往往需要得到那些最相似或者相似度超过某个下界的文档对。如果是这样，我们只需要关注那些可能的相似对，而不需要研究所有的文档对。

目前对这类问题的处理存在着一个称为局部敏感哈希（locality-sensitive hashing, LSH）或邻近搜索(near-neighbor search)的一般性理论。

4.1 面向minhasing signature的LSH

LSH的一般做法是对目标项进行多次哈希处理，使得相似项会比不相似项更可能哈希到同一个桶中。然后将至少有一次哈希到同一个桶中的文档对看成是候选对(candidate pair),我们只检查这些候选对的相似度。这里会出现伪正例和伪反例。

假设我们已经计算出了目标项的最小哈希签名矩阵SIG，

其中一个有效的处理方法是将签名矩阵SIG划分成b个行条（band），每个行条由R/b = r 行组成。对于每个行条r,存在一个哈希函数能够将行条中的列向量映射到某个大数目范围的桶中。可以对所有的行条使用相同的哈希函数，但是每个行条却需要使用一个独立的桶数组。

现在进行代码测试：

首先增加两个哈希函数：

int h3(int r)
{
	return (2*r+1)%5;
}
int h4(int r)
{
	return (r+2)%5;
}
//如何设置由函数作为数组元素的数组
int (*hashf[4])(int);
void inithash()
{
	hashf[0]=h1;
	hashf[1]=h2;
	hashf[2]=h3;
	hashf[3]=h4;
}

在上一节的代码中增加如下代码：来计算候选对

//used to get candidate
const int B=2;
int candidate[B][setN];
int RL[setN][setN];
//计算候选对RL[i][j]
void getCandidate(int R)//get candidate for LSH
{
	int row = 0;
	if(R%B != 0)
	{
		return;
	}
	row = R/B;

	for(int i=0;i<B;i++)
	{
		for(int m=0;m<setN;m++)
		{
			for(int r =2*i;r<(R/B+2*i);r++)//row(0,R/B=2),then 2,4, from 2*i, to R/B+2*i
			{
				candidate[i][m]+=h1(SIG[r][m]-1);
			}
		}
		for(int m=0;m<setN;m++)
		{
			for(int k=m+1;k<setN;k++)
			{
				if(candidate[i][m]==candidate[i][k] && RL[m][k]==0)//if candidae equal, then candidata pair m,k= 1
				{
					RL[m][k]=1;
				}

			}
		}
	}

}

修改函数countForSIM

template<int C,int map[][C]>
void countForSIM(int R, bool flag=false)//flag used to control if it will use the LSH
{
	reset(x);
	reset(xpy);
	for(int r=0;r<R;r++)
	{
		for(int m = 0;m<C;m++)
		{
	
			for(int j=m+1;j<C;j++)
			{
				if(flag==true)//if it will use LSH
				{
					if(RL[m][j]==0)
					{
						continue;
					}
				}
				if(map[r][m]==1 && map[r][j]==1)
				{
					x[m][j]++;
					xpy[m][j]++;
				}
				else if(map[r][m]==1 || map[r][j]==1)
				{
					xpy[m][j]++;
				}

			}				
		}
	}
}

调用如下的测试代码：

	cout<<"original set................................."<<endl;
	printM<setN,matrix>(5);
	initSIG();
	//printM<setN,SIG>(2);
	inithash();
	minHash(setN,4,5);
	cout<<"hash signature set..........................."<<endl;
	printM<setN,SIG>(4);

    countForSIM<setN,matrix>(5);
	getSIM1();
	cout<<"SIM1........................................."<<endl;
	printMd<setN,SIM1>(setN);

    getCandidate(4);
	cout<<"candidate........................................."<<endl;
	printM<setN,candidate>(2);
    cout<<"RL........................................."<<endl;
	printM<setN,RL>(setN);

	countForSIM<setN,SIG>(4,true);
	getSIM2();
	cout<<"SIM2........................................."<<endl;
	printMd<setN,SIM2>(setN);

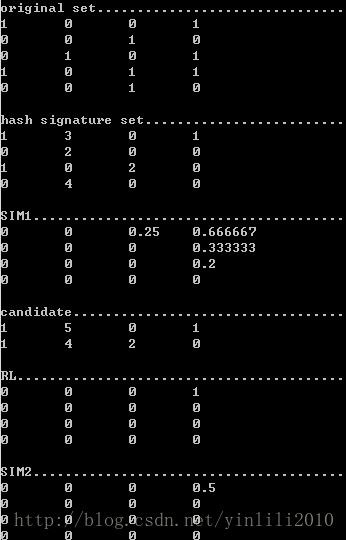
得到如下的结果：

整个测试的可执行文件参看如下链接：http://pan.baidu.com/s/1D7daY