MST_prim
关于最小生成树,在本blog的MST_kruskal算法中已经介绍过了,这里介绍另外一种算法即prim算法
写讲一下prim算法的基本思想
1.初始化所有结点都为未访问
2.从图中任选一点,加入到集合V中并标记它为已访问
3.从未标记的点中选取到集合V中的顶点中距离最小的,并加入到集合V中,标记它已访问。
4,.重复3步骤直到所有的点都选入到集合V中
这里讲一下上述步骤的实现
1.初始化vis数组为false,数组下标表示结点的编号,设置距离数组dis的值都为inf(不合理的值)。
2.选1结点,标记vis[1]=true,更新距离数组,dis[i] = map[1][i];(这里采用邻接矩阵存图)
3.从距离数组中选dis最小的,假设是k,标记它为访问vis[k]=true,然后以k结点为跳板更新距离数组if(!vis[i]&&dis[i]>map[k][i]) dis[i]=map[k][i]。(是不是和dijkstra算法一样啊,只是多了一个!vis[i],没学过kruskal算法的跳过)
4,重复3步骤直到所有的结点选完(可以设置一个计数器来判断嘛)
下面举个例子讲一下算法的流程
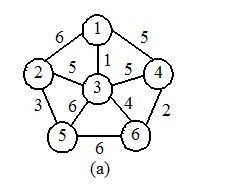
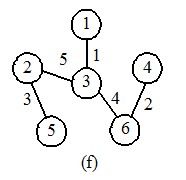
a为原图,f为MST(最小生成树)
1.初始化距离数组dis,标记数组vis.
2.选1结点,设置vis[1]=true,更新距离数组dis[2]=6,dis[3]=1,dis[4]=5
3.选距离最小的3结点,以3结点为跳板更新距离数组,dis[2]本来是6现在有了3可以更新成5了,同理dis[6]=4
相信读者都明白了,这里不继续往下说了,贴下模板
#include <iostream>
#include <cstdio>
#include <cstring>
#define INF 100000
using namespace std;
struct Graph
{
int vexnum;
int map[501][501];
};
bool vis[501];
int dis[501],num1;
Graph G;
int prim()
{
int tem;
int result=0;//记录MST的总权值
int num1;
memset(vis,false,sizeof(vis));
vis[1] = true;
for(int i=2;i<=G.vexnum;i++)
dis[i]=G.map[1][i];
num1 = 1;
while(num1<G.vexnum)
{
int min = INF;
for(int i=1;i<=G.vexnum;i++)//从剩余的点中找到已有的点的集合中距离最小的点
{
if(!vis[i]&&dis[i]<min)
{
min = dis[i];
tem = i;
}
}
if(min==INF&&num1<G.vexnum) return -1;//可以选的都选完了,但是没全部选进来(就是说明这个图不是连通图)
result += min;
vis[tem] = true;
for(int i=1;i<=G.vexnum;i++)//更新距离
{
if(!vis[i]&&dis[i]>G.map[tem][i])
{
dis[i]=G.map[tem][i];
}
}
num1++;
}
return result;
}
最后提一点:因为kruskal是选边所以适合于点多边少的图,而prim算法是选点,所以适合点少边多的图。
推荐题目http://acm.hdu.edu.cn/showproblem.php?pid=3371(晕死,卡重边,用kruskal算法可能超时:点少边多)