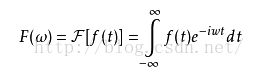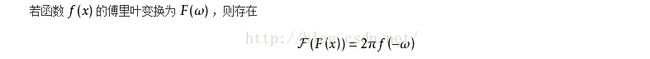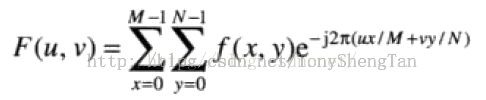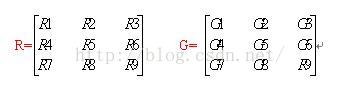数字图像处理2--数学基础(傅立叶,拉普拉斯,卷积,差分计算)
本文是为了方便各位在图像处理中理解基本的数学模型及其表达式等,所以我们不对该类数学基础在信号与系统等方面的运用。欢迎评论补充!
傅立叶变换
非周期性连续信号 傅立叶变换(Fourier Transform)
非周期性离散信号 离散时域傅立叶变换(Discrete Time Fourier Transform)
周期性离散信号 离散傅立叶变换(Discrete Fourier Transform) -DFT
若 f(t)是t的周期函数,如果t满足狄里赫莱条件:在一个以2T为周期内f(X)连续或只有有限个第一类间断点,附f(x)单调或可划分成有限个单调区间,则F(x)以2T为周期的傅里叶级数收敛,和函数S(x)也是以2T为周期的周期函数,且在这些间断点上,函数是有限值;在一个周期内具有有限个极值点;绝对可积。则有下图①式成立。称为积分运算f(t)的傅立叶变换。
傅里叶变换可以化复杂的卷积运算为简单的乘积运算,从而提供了计算卷积的一种简单手段。
线性性质
快速傅立叶变换
二维傅立叶变换
二维傅里叶变换一般用在数字图像处理中,一般是二维的灰度图像f(x,y)变换到频域F(u,v)。在频谱图中,中心部分(uv坐标系中点(0,0)附近)表示原图像中的低频部分,是图像中灰度变化不太快的成分,反映了图像的主体框架;而频谱的四周,也即是高频区域是图像中灰度变化较快的成分,一般反映着图像中的椒盐噪声(突发性的白点或黑点)或者是图像内部变化剧烈的边缘成分。如果原始图像具有十分明显的规律,例如将一个简单图样有规律的平移并填满整个图形,那么其频谱一般表现为坐标原点周围的一圈亮点。
常见性质
卷积和相关理论
卷积核:卷积时使用到的权,用一个矩阵表示,该矩阵与使用的图像区域大小相同,其行、列都是奇数,是一个权矩阵。
1、卷积示例:
假设3 * 3的像素区域R与卷积核G分别为:
则卷积运算为:
R5(中心像素)=R1G1 + R2G2 + R3G3 + R4G4 + R5G5 + R6G6 + R7G7 + R8G8 + R9G9
2、使用模板处理图像时涉及到的问题:
边界问题:当处理图像边界像素时,卷积核与图像使用区域不能匹配,卷积核的中心与边界像素点对应,卷积运算将出现问题。
处理办法:
A.忽略边界像素,即处理后的图像将丢掉这些像素。
B.保留原边界像素,即copy边界像素到处理后的图像。
3、常用模板:
连续空间的卷积定义是f(x)与g(x)的卷积是f(t-x)g(x)在t从负无穷到正无穷的积分值.t-x要在f(x)定义域内,所以看上去很大的积分实际上还是在一定范围的.
实际的过程就是f(x)先做一个Y轴的反转,然后再沿X轴平移t就是f(t-x),然后再把g(x)拿来,两者乘积的值再积分.想象一下如果g(x)或者f(x)是个单位的阶越函数.那么就是f(t-x)与g(x)相交部分的面积.这就是卷积了.
卷积运算满足交换律,也就是说:f与g进行卷积完全等于g与f进行卷积。
由两个函数f和g进行卷积而得到的函数f*g,一般要比原来的f和g都要光滑。所以在图像处理中对图像进行卷积后会使原图像模糊。
因为卷积具有平滑作用。
那么在图像中卷积是什么意思呢,就是图像就是图像f(x),模板是g(x),然后将模版g(x)在模版中移动,每到一个位置,就把f(x)与g(x)的定义域相交的元素进行乘积并且求和,得出新的图像一点,就是被卷积后的图像.模版又称为卷积核.卷积核做一个矩阵的形状。