树形DP图画入门(HDU1520) (FZU1615)
一棵树每个节点有一个权值,保证父亲节点与孩子节点不能同时出现,求出现的节点最大权值。
HDU 1520 http://acm.hdu.edu.cn/showproblem.php?pid=1520
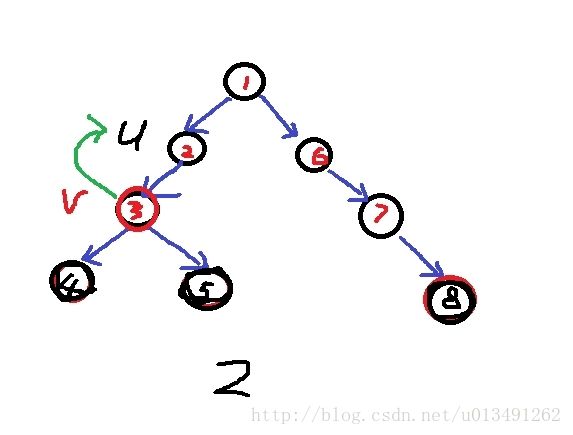
图1 : 走到叶子节点4 , 回退 ;
此时 , dp[4][go] , dp[4][notgo] 已有最优解 。
图2 : u -> v , v计算完回退的时候, dp[v][go] , dp[v][notgo] 已有最优解 。
注意: 1 、以任意节点为根节点都可以,因为是一颗同构树。
2、father - > u - > v
防止出现 father - > u - > father
const int Max_N = 6008 ;
#define go 0
#define notgo 1
vector<int> List[Max_N] ;
int N ;
int dp[Max_N][2] ;
void dfs(int u , int father){
int i , v ;
for(i = 0 ; i < List[u].size() ; i++){
v = List[u][i] ;
if(v == father)
continue ;
dfs(v , u) ;
dp[u][go] += dp[v][notgo] ;
dp[u][notgo] += max(dp[v][go] , dp[v][notgo]) ;
}
}
int main(){
int i , u , v ;
while(cin>>N){
memset(dp , 0 , sizeof(dp)) ;
for(i = 1 ; i <= N ; i++) List[i].clear() ;
for(i = 1 ; i <= N ; i++)
scanf("%d" ,&dp[i][go]) ;
while(scanf("%d%d" ,&u ,&v)){
if(u == 0 && v ==0)
break ;
List[u].push_back(v) ;
List[v].push_back(u) ;
}
dfs(1 , -1) ;
printf("%d\n" , max(dp[1][go] , dp[1][notgo])) ;
/* 以任意节点为根节点都可以,因为是一颗同构树 。
dfs(2 , -1) ;
printf("%d\n" , max(dp[2][go] , dp[2][notgo])) ;*/
}
return 0 ;
}
http://acm.fzu.edu.cn/problem.php?pid=1615
(a , b , w) a,b 都去,则损失w 。求最大值。
const int Max_N = 10008 ;
#define go 0
#define notgo 1
struct Edge{
int v ;
int w ;
Edge(){}
Edge(int i , int j):v(i),w(j){}
};
map<string ,int> name ;
vector<Edge>List[Max_N] ;
int dp[Max_N][2] ;
int N ;
void dfs(int u){
int i , v , w ;
for(i = 0 ; i < List[u].size() ; i++){
v = List[u][i].v ;
w = List[u][i].w ;
dfs(v) ;
dp[u][notgo] += max(dp[v][go] , dp[v][notgo]) ;
dp[u][go] += max(dp[v][notgo] , dp[v][go] - w) ;
}
}
int main(){
int i , w , u , v , root ;
char str[12] , str2[12] ;
while(scanf("%d" ,&N) != EOF){
name.clear() ;
for(i = 1 ; i <= N ; i++) List[i].clear() ;
for(i = 1 ; i <= N ; i++){
scanf("%s %d" ,str , &dp[i][go]) ;
name[string(str)] = i ;
dp[i][notgo] = 0 ;
}
for(i = 1 ; i < N ; i++){
scanf("%s%s%d" ,str ,str2 ,&w) ;
u = name[string(str)] ;
if(i == 1)
root = u ;
v = name[string(str2)] ;
List[u].push_back(Edge(v , w)) ;
}
dfs(root) ;
printf("%d\n" ,max(dp[root][go] , dp[root][notgo])) ;
}
return 0 ;
}