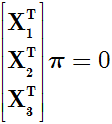3D射影几何和射影变换

点

三维空间的点X用齐次坐标表示为一个4维矢量X=(x₁, x₂, x₃,x₄)^T. 当x₄≠0时表示IP³中非齐次坐标为(X, Y, Z)^T的点, 其中X=x₁/ x₄, Y= x₂/ x₄, Z= x₃/x₄. 当x₄=0时表示无穷远点.

IP³上的射影变换是由4×4非奇异矩阵给出, 它是关于齐次4维矢量的线性变换: X’=HX. 变换矩阵H是齐次的并有15个自由度. 矩阵的16个元素扣去一个全局尺度就是它的自由度数. 与平面射影变换的情况一样, 该映射是保线变换( 直线被映射到直线) , 它保留诸如直线与平面的交点等关联关系与接触的阶.

平面

三维空间中平面可以写成π₁X+π₂Y+π₃Z+π₄=0. 显然, 该等式乘上一个非零常数仍然成立, 所以只有平面方程稀疏的三对独立比率是有意义的. 因此在三维空间中一张平面有3个自由度. 平面的齐次表示是4维矢量π=(π₁,π₂, π₃, π₄)^T.  齐次化可以表示为π₁x₁+π₂x₂+π₃ x₃+π₄ x₄=0, 或者更简洁π^TX=0. 它表示点X在平面π上. π的前三个分量对应于欧式几何中平面的法线, 用非齐次记号可以写成三维矢量形式下熟知的平面方程:

其中,  n=(π ₁ ,π ₂ , π ₃ ) ^T ,  d=π₄ . 在此式中 d/||n|| 是原点到平面的距离,  (nX+d)/||n|| 是点到平面的距离 (这里暂时用X表示三维点的非齐次表示).

直线

两点的连线或两平面的相交定义一条直线. 在三维空间中, 直线有四个自由度(把直线看成由它与两正交平面的交点来定义, 其中每张平面上的交点有两个参数来确定, 所以一共有四个自由度). 三维空间中的直线表示相当难处理, 因为4个自由度的对象应该用5维齐次矢量表示(二维空间中的直线有两个自由度, 斜率和截距), 但问题是5维齐次矢量与表示点和平面的4维齐次矢量很难同时在数学表达式中使用.

在IP³中, 平面, 点, 直线之间存在许多几何关系, 例如

1. 平面可由一般位置的三个点或一条直线与一个点的联合来唯一确定(一般位置指三点不共线或在后一种情况下指点不在直线上).

2. 两张不同的平面相交于唯一的直线.

3. 三张不同的平面相交于唯一的点.

由于直线的代数表示不再像IP²中用3维矢量表示那样简单, 这里不给出介绍 (可参考多视图几何2.2.2).

三点确定一张平面. 设三点X_i在平面π上, 那么每点满足π^TX_i=0, i=1,2,3, 将这些方程联合成一个矩阵方程

因为一般位置上的三点线性无关, 所以由它们作为行组成的3×4矩阵的秩为3. 由这些点所定义的平面π作为它的1维右零空间被唯一的确定(相差一个常数因子). 如果矩阵的秩为2, 则零空间是2维的, 那么这些点是共线的, 并定义了以共线点组成的直线为轴的一个平面束. 

在IP²中, 点与线对偶, 过两点x, y的直线可以类似地用求以x^T和y^T为行组成的2×3矩阵的零空间获得. 当然也可以由矢量代数直接得到一个更便利的公式I=x×y.

三平面确定一点. 三张平面π_i的交点X可以通过求以三张平面为行的3×4矩阵的右零空间直接计算出来:

类似于2D射影变换, 3D射影变换有欧式(6 dof), 相似(7 dof), 仿射(12 dof) 和射影(15 dof). 射影变换的15个自由度分别如下: 7个用于相似变换(旋转3个, 平移3个, 均匀缩放1个), 五个用于仿射变换, 三个用于射影变换.