B tree and LSM tree

本文主要介绍了B+ tree和LSM tree，从seek和transfer的角度看Hbase为什么选择了LSM tree，而不是像大多数RDBMS那样使用B+ tree，在Hbase里面LSM tree这种结构其实就是由HLog + Memstore + StoreFile构成，HLog保存了顺序写入磁盘的日志，Memstore能够保存最近的数据，StoreFile负责存储Memstore flush的数据，另外背后有一些服务线程默默的做了很多事情，比如针对store files的compaction, 针对region的split, hlog file的roller等等。

Before we look into the architecture itself, however, we will first address a more fundamental difference between typical RDBMS storage structures and alternative ones. Specifically, we are going to have a quick look into B-trees, or rather B+ trees, as they are commonly used in relational storage engines, and Log-Structured Merge Trees, which (to some extent) form the basis for Bigtable's storage architecture, as discussed in the section called “Building Blocks”.

 Note
 Please note that RDBMSs are not limited to use B-tree type structures, nor do all NoSQL solutions use different architectures. You will find a colorful variety of mix-and-match technologies, but with one common objective: use the best strategy for the problem at hand. We will see below why Bigtable uses an approach similar to LSM-trees to just achieve that.

B+ trees

B+ trees have some specific features that allow for efficient insertion, lookup, and deletion of records that are identified by keys. They represent dynamic, multilevel indexes with lower and upper bounds as far as the number of keys in each segment (also called page) is concerned. Using these segments, they achieve a much higher fanout compared to binary trees, resulting in a much lower number of IO operations to find a specific key.

In addition, they also enable you to do range scans very efficiently, since the leaf nodes in the tree are linked and represent an in-order list of all keys, avoiding more costly tree traversals. That is one of the reasons why they are used for indexes in relational database systems.

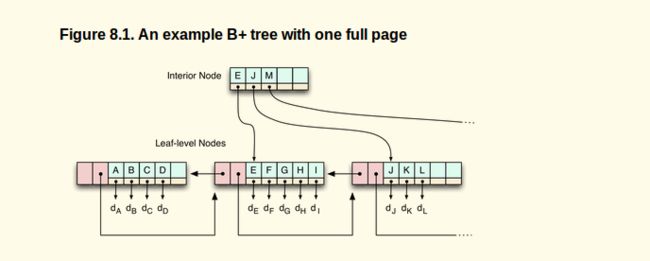
In a B+ tree index, you get locality on a page-level (where page is synonymous to "block" in other systems): for example, the leaf pages look something like:

[link to previous page]

[link to next page]

key1 → rowid

key2 → rowid

key3 → rowid

In order to insert a new index entry, say key1.5, it will update the leaf page with a new key1.5 → rowid entry. That is not a problem until the page, which has a fixed size, exceeds its capacity. Then it has to split the page into two new ones, and update the parent in the tree to point to the two new half-full pages. See Figure 8.1, “An example B+ tree with one full page” for an example of a page that is full and would need to be split when adding another key.

The issue here is that the new pages aren't necessarily next to each other on disk. So now if you ask to query a range from key 1 to key 3, it's going to have to read two leaf pages which could be far apart from each other. That is also the reason why you will find an OPTIMIZE TABLE commands in most B+-tree based layouts - it basically rewrites the table in-order so that range queries become ranges on disk again.

Log-Structured Merge-Trees

LSM-trees, on the other hand, follow a different approach. Incoming data is stored in a log file first, completely sequentially. Once the log has the modification saved, it then updates an in-memory store that holds the most recent updates for fast lookup.

When the system has accrued enough updates and starts to fill up the in-memory store, it flushes the sorted list of key → record pairs to disk, creating a new store file. At this point, the updates to the log can be thrown away, as all modifications have been persisted.

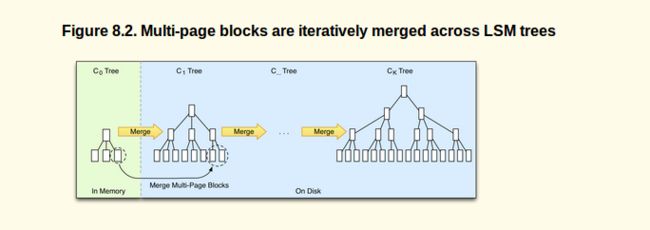
The store files are arranged similar to B-trees, but are optimized for sequential disk access where all nodes are completely filled and stored as either single-page or multi-page blocks. Updating the store files is done in a rolling merge fashion, i.e., the system packs existing multi-page blocks together with the flushed in-memory data until the block reaches it full capacity.

Figure 8.2, “Multi-page blocks are iteratively merged across LSM trees” shows how a multi-page block is merged from the in-memory tree into the next on-disk one. Eventually the trees are kept merging into the larger ones.

As there are more flushes happening over time, creating many store files, a background process aggregates the files into larger ones so that disk seeks are limited to only a few store files. The on-disk tree can also be split into separate ones to spread updates across multiple store files. All of the stores are always sorted by the key, so no reordering is required ever to fit new keys in between existing ones.

Lookups are done in a merging fashion where the in-memory store is searched first, and then the on-disk store files next. That way all the stored data, no matter where it currently resides, forms a consistent view from a client's perspective.

Deletes are a special case of update wherein a delete marker is stored that is used during the lookup to skip "deleted" keys. When the pages are rewritten asynchronously, the delete markers and the key they mask are eventually dropped.

An additional feature of the background processing for housekeeping is the ability to support predicate deletions. These are triggered by setting a time-to-live (TTL) value that retires entries, for example, after 20 days. The merge processes will check the predicate and, if true, drop the record from the rewritten blocks.

The fundamental difference between the two, though, is how their architecture is making use of modern hardware, especially disk drives.

 Seek vs. Sort and Merge in Numbers[85]

 For our large scale scenarios computation is dominated by disk transfers. While CPU, RAM and disk size double every 18-24 months the seek time remains nearly constant at around 5% speed-up per year.

 As discussed above there are two different database paradigms, one is Seek and the other Transfer. Seek is typically found in RDBMS and caused by the B-tree or B+ tree structures used to store the data. It operates at the disk seek rate, resulting in log(N) seeks per access.

 Transfer on the other hand, as used by LSM-trees, sorts and merges files while operating at transfer rate and takes log(updates) operations. This results in the following comparison given these values:

 10 MB/second transfer bandwidth

 10 milliseconds disk seek time

 100 bytes per entry (10 billion entries)

 10 KB per page (1 billion pages)

 When updating 1% of entries (100,000,000) it takes:

 1,000 days with random B-tree updates

 100 days with batched B-tree updates

 1 day with sort and merge

 We can safely conclude that at scale seek is simply inefficient compared to transfer.

Comparing B+ trees and LSM-trees is about understanding where they have their relative strengths and weaknesses. B+ trees work well until there are too many modifications, because they force you to perform costly optimizations to retain that advantage for a limited amount of time. The more and faster you add data at random locations, the faster the pages become fragmented again. Eventually you may take in data at a higher rate than the optimization process takes to rewrite the existing files. The updates and deletes are done at disk seek rates, and force you to use one of the slowest metric a disk has to offer.

LSM-trees work at disk transfer rates and scale much better to handle vast amounts of data. They also guarantee a very consistent insert rate, as they transform random writes into sequential ones using the log file plus in-memory store. The reads are independent from the writes, so you also get no contention between these two operations.

The stored data is always in an optimized layout. So, you have a predictable and consistent bound on number of disk seeks to access a key, and reading any number of records following that key doesn't incur any extra seeks. In general, what could be emphasized about an LSM-tree based system is cost transparency: you know that if you have five storage files, access will take a maximum of five disk seeks. Whereas you have no way to determine the number of disk seeks a RDBMS query will take, even if it is indexed.