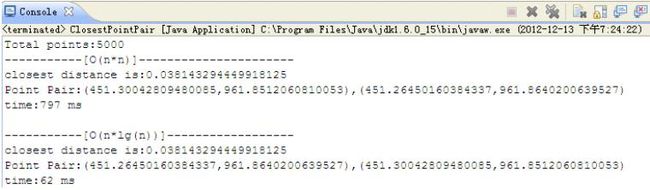
平面点对实验

OJ地址：POJ3714    ZOJ2107     HDU1007

参考：点击打开链接

本人的实验程序：

package sse.algorithm;

import java.util.ArrayList;
import java.util.List;

public class ClosestPointPair {
	/*
	 * 实验：分治法O(n*lg(n))时间内求二维点集最近点对算法
	 * 作者：xxxxxxx098
	 * 时间：2012-12-07 19:00
	 */
    
    /*
     * boolean Cpair2(S,d)算法步骤：
     * n = |S|;
     * if(n < 2) return false;
     * 将点集 S 中的点依其 y 坐标值排序,然后作以下事情
     * 1.  m = S中各点x横坐标的中位数
     *     构造S1，S2
     *     S1 = {p in S| x(p) <= m}, S2 = {p in S| x(p) > m}
     * 2.  Cpair2(S1,d1) 
     *     Cpair2(S2,d2)   
     * 3.  dm = min(d1,d2)
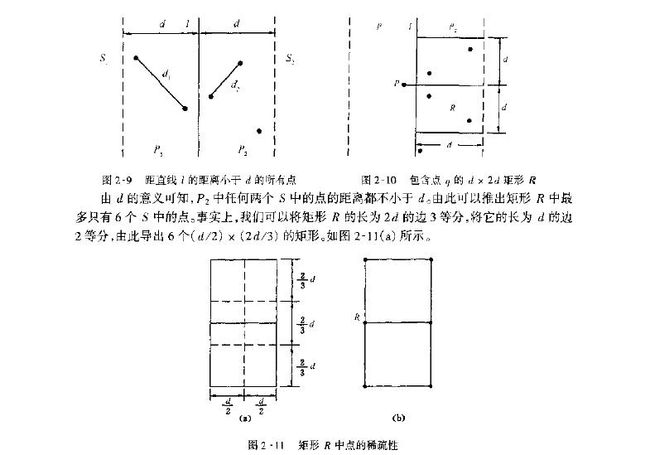
     * 4.  设P1是S1中距离垂直分割线l的距离在 dm 之内的所有组成的集合，
     *     P2是S2中距离垂直分割线l的距离在 dm 之内的所有点组成的集合，
     * 5.  通过扫描 P1 以及对于 P1 中每个点检查 P2 中与其距离在 dm 之内的所有点(最多6个)可以完成合并
     *     当 P1中 扫描指针逐次向上移动时，P2中的扫描指针可在宽为 2dm 的一个区间内移动
     *     设dl是按这种扫描方式找到的点对间的最小距离
     * 6.  d = min(dm,dl)
     *     return true;
     *       
     */
    
    public Point p1;//最近点对中p1的坐标
    public Point p2;//最近点对中p1的坐标
    public double d = Double.MAX_VALUE;//点对间的距离
    //public Logger log = Logger.getLogger(ClosestPointPair.class);
    
    public ClosestPointPair(){}
    
    /*
     * 返回List[start..end]中第order小的元素的x属性的值
     */
    public double find(List<Point> S,int start,int end,int order){
        if(start>end || order>end-start+1){
            return -1;
        }
        int res = partitionX(S,start,end);
        int k = res-start+1;
        if(k == order)
            return S.get(res).x;
        else if(k > order)
            return find(S,start,res-1,order);
        else
            return find(S,res+1,end,order-k);
    }
    
    // 依x 坐标值寻找划分元的位置,返回划分元在S中的下标
    public static int partitionX(List<Point> S,int low, int high){
        int randomPivot = low+ (int)(Math.random()*(high-low+1));
        double pivotValue = S.get(randomPivot).x;
        
        while(low < high){
            //从右边找比枢纽元素小的的元素
            while((low < high) && (S.get(high).x >= pivotValue)){
                high--;
            }
            //交换两个元素
            S.get(low).swapWith(S.get(high));
            //从左边找比枢纽元素大的的元素
            while((low < high) && (S.get(low).x <= pivotValue)){
                low++;
            }
            S.get(high).swapWith(S.get(low));
        }
        return low;
    }
    
    /*
     * 以下完成把点集 S 中的点依其 y 坐标值排序
     */
    public static void sortPointListByY(List<Point> S,int low,int high){
        if(low < high){
            int mid =partitionY(S,low,high);
            sortPointListByY(S,low,mid-1);
            sortPointListByY(S,mid+1,high);
        }
    }
    
    // 依y 坐标值寻找划分元的位置
    public static int partitionY(List<Point> S,int low, int high){
        int randomPivot = low+ (int)(Math.random()*(high-low+1));
        double pivotValue = S.get(randomPivot).y;
        
        while(low < high){
            //从右边找比枢纽元素小的的元素
            while((low < high) && (S.get(high).y >= pivotValue)){
                high--;
            }
            //交换两个元素
            S.get(low).swapWith(S.get(high));
            //从左边找比枢纽元素大的的元素
            while((low < high) && (S.get(low).y <= pivotValue)){
                low++;
            }
            S.get(high).swapWith(S.get(low));
        }
        return low;
    }
    /*
     * 以下求二维平面的最近点对
     * Cpair2(S1,d1) 
     * Cpair2(S2,d2)   
     * dm = min(d1,d2)
     * 设P1是S1中距离垂直分割线l的距离在 dm 之内的所有点组成的集合，
     *   P2是S2中距离垂直分割线l的距离在 dm 之内的所有点组成的集合，
     * 
     * 通过扫描 P1 以及对于 P1 中每个点检查 P2 中与其距离在 dm 之内的所有点(最多6个)可以完成合并
     * 当 P1中 扫描指针逐次向上移动时，P2中的扫描指针可在宽为 2dm 的一个区间内移动
     * 设dl是按这种扫描方式找到的点对间的最小距离
     * 
     * d = min(dm,dl)
     * 
     */
    public double Cpair2(List<Point> S) {
        
        if(S.size() < 2)return Double.MAX_VALUE;
        List<Point> S1 = new ArrayList<Point>();
        List<Point> S2 = new ArrayList<Point>();
        
        double median = find(S, 0, S.size()-1, (int)((S.size()+ 1)/2));
        
        dividePoints(S,median,S1,S2);//将点集一分为二
        
        double d1 = Cpair2(S1);
        double d2 = Cpair2(S2);
        double dm = Math.min(d1, d2);
        
        List<Point> P1 = new ArrayList<Point>();
        List<Point> P2 = new ArrayList<Point>();
        narrowToP1P2(S1,S2,median,dm,P1,P2);//缩小S1，S2的范围至P1，P2
        
        //扫描P1
        double tmp;
        Point point1 = null;
        Point point2 = null;
        for(int i=0;i<P1.size();i++){
            point1 = P1.get(i);
            //以下获得P2中的候选点，count计数最多6个
            for(int j=0,count=0;j<P2.size() && count<6;j++){
                point2 = P2.get(j);
                if(Math.abs(point1.y - point2.y) <= dm){
                    count++;
                    //逐一检查候选点
                    tmp = point1.distanceTo(point2);
                    if(tmp < this.d){
                        this.d = tmp;
                        this.p1 = point1;
                        this.p2 = point2;
                    }
                }
            }
        }
        return Math.min(dm, this.d);
    }
	
	//按S中x坐标的总位数，把S划分为S1，S2
    //其中，S1 = {p in S| x(p) <= m}, S2 = {p in S| x(p) > m}
	public void dividePoints(List<Point> S,double median,List<Point> S1,List<Point> S2){
	    for(int i=0;i<S.size();i++){
	        Point p = S.get(i);
	        if(p.x <= median)
	            S1.add(p);
	        else
	            S2.add(p);
	    }
    }
	
	//P1是S1中距离垂直分割线l的距离在 dm 之内的所有点组成的集合，
    //P2是S2中距离垂直分割线l的距离在 dm 之内的所有点组成的集合，
	public void narrowToP1P2(List<Point> S1,List<Point> S2,double median,double dm,List<Point> P1,List<Point> P2){
	    for(int i=0;i<S1.size();i++){
	        if((median - S1.get(i).x) <= dm){
	            P1.add(S1.get(i));
	        }
	    }
	    
	    for(int i=0;i<S2.size();i++){
            if((S2.get(i).x - median) <= dm){
                P2.add(S2.get(i));
            }
        }
	}
	/*
	 * 蛮力法求最近点对
	 * 用于对比验证试验的正确性
	 */
	public double rudeGet(List<Point> S){
	    if(S.size()<2)return Double.MAX_VALUE;
	    double res=Double.MAX_VALUE;
	    double tmp;
	    Point pt1,pt2;
	    for(int i=0;i<S.size()-1;i++){
	        pt1 = S.get(i);
	        for(int j=i+1;j<S.size();j++){
	            pt2 = S.get(j);
	            tmp = pt1.distanceTo(pt2);
	            if(tmp < res){
	                res = tmp;
	                this.d = tmp;
	                this.p1 = pt1;
	                this.p2 = pt2;
	            }
	        }
	    }
	    return res;
	}
	public double randomDouble(){
	    return Math.random()*1000;
	}

	public static void main(String[] args) {
	    int TOTALPOINTS = 5000;//要生成的点的总数
	    ClosestPointPair cp = new ClosestPointPair();
	    ClosestPointPair cp2 = new ClosestPointPair();
	    
	    //先随机生成0-1000内的坐标值，暂存到二维数组
	    double arraypoint[][] = new double[TOTALPOINTS][2];
	    for(int i=0;i<TOTALPOINTS;i++)
	        for(int j=0;j<2;j++)
	            arraypoint[i][j]= cp.randomDouble();
	    //考虑到点可能有很多，故将点集存到链表中
	    List<Point> S = new ArrayList<Point>();
	    List<Point> S_backup = new ArrayList<Point>();
	    for(int i=0;i<arraypoint.length;i++){
	        S.add(new Point(arraypoint[i][0],arraypoint[i][1]));
	        S_backup.add(new Point(arraypoint[i][0],arraypoint[i][1]));
	    }
	    //预处理：按y坐标排序
	    sortPointListByY(S, 0, S.size()-1);
	    sortPointListByY(S_backup, 0, S_backup.size()-1);
	    System.out.println("Total points:"+TOTALPOINTS);
	    //统计蛮力法的时间
	    long time1,time2;
	    time1=System.currentTimeMillis();
	    double res = cp.rudeGet(S);
	    time2=System.currentTimeMillis();
	    System.out.println("-----------[O(n*n)]----------------------\nclosest distance is:"
	            +res+"\nPoint Pair:"+cp.p1+","+cp.p2+"\ntime:"+(time2-time1)+" ms");
	    //统计分治法的时间
	    time1=System.currentTimeMillis();
	    res = cp2.Cpair2(S_backup);
	    time2=System.currentTimeMillis();
	    System.out.println("\n-----------[O(n*lg(n))]------------------\nclosest distance is:"
	            +res+"\nPoint Pair:"+cp2.p1+","+cp2.p2+"\ntime:"+(time2-time1)+" ms");
    }
}

class Point{
    public double x;
    public double y;
    public Point(){}
    public Point(double x,double y){
        this.x=x;
        this.y=y;
    }
    public double distanceTo(Point p){ //假设p != null
        return Math.sqrt((x-p.x)*(x-p.x) + (y-p.y)*(y-p.y));
    }
    public void swapWith(Point p){
        double tmpx=p.x, tmpy=p.y;
        p.x = this.x;
        p.y = this.y;
        this.x = tmpx;
        this.y = tmpy;
    }
    public String toString(){
        return "("+x+","+y+")";
    }
}