AVL树实现

AVL 树，相当于在二叉搜索树(BST)中再增加一个平衡因子的变量，用来存储当前结点左右子树高度的差值

struct avl_node {
    struct avl_node *parent;
    struct avl_node *left;
    struct avl_node *right;
    int key;
    /* the same as bst_node on the above */

    int factor;                 /* left_height - right_height */
};


struct avl_root {
    struct avl_node *avl_node;
};

由AVL定义可见，其平衡因子只可能有三种值0，-1，1；在插入、删除时，结点的平衡因子可能会变化成2、-2，称此结点为不平衡结点，这时就需要对AVL 树的进行调整。

AVL 树的平衡调整

AVL不平衡结点最多有四种可能，见下图：

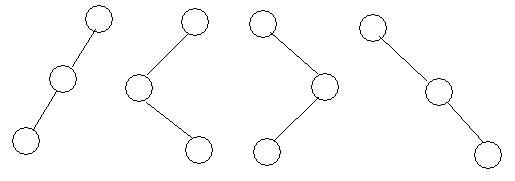
称之为LL，LR，RL，RR，对于LL，RR，只需要一次旋转就行了，对于 LR和RL ，需要多做一次旋转

static struct avl_node* avl_balance(struct avl_node *y, struct avl_root *root)
{
    struct avl_node *x, *w;

    if (y->factor == 2) {      /* left is high */
        x = y->left;
        if (x->factor == 1) {  /* LL */
            bst_rotate_right((struct bst_node *)y, (struct bst_node **)&root->avl_node);
            x->factor = y->factor = 0;
            return x;
        }
        else if (x->factor == -1) { /* LR */
            w = x->right;
            bst_rotate_left((struct bst_node *)x, (struct bst_node **)&root->avl_node);
            bst_rotate_right((struct bst_node *)y, (struct bst_node **)&root->avl_node);
            if (w->factor == 0) 
                x->factor = y->factor = 0;
            else if (w->factor == -1)
                x->factor = 1, y->factor = 0;
            else
                x->factor = 0, y->factor = -1;
            w->factor = 0;
            return w;
        }
        else {                  /* factor == 0, only used for delete */
            bst_rotate_right((struct bst_node *)y, (struct bst_node **)&root->avl_node);
            x->factor = -1;
            y->factor = 1;
            return x;
        }
    }
    else {                      /* right is high, factor is -2 */
        x = y->right;
        if (x->factor == -1) {   /* RR */
            bst_rotate_left((struct bst_node *)y, (struct bst_node **)&root->avl_node);
            x->factor = y->factor = 0;
            return x;
        }
        else if (x->factor == 1) { /* RL */
            w = x->left;
            bst_rotate_right((struct bst_node *)x, (struct bst_node **)&root->avl_node);
            bst_rotate_left((struct bst_node *)y, (struct bst_node **)&root->avl_node);
            if (w->factor == 0)
                x->factor = y->factor = 0;
            else if (w->factor == 1)
                x->factor = -1, y->factor = 0;
            else
                x->factor = 0, y->factor = 1;
            w->factor = 0;
            return w;
        }
        else {                 /* factor == 0, only used for delete */
            bst_rotate_left((struct bst_node *)y, (struct bst_node **)&root->avl_node);
            x->factor = 1;
            y->factor = -1;
            return x;
        }
    }
    return 0;
}

此函数为AVL平衡调整函数，为理解AVL树的精髓。它分成了两大段，一段处理平衡因子为2，一段处理平衡因子为-2，以下详细描述平衡因子为2的情况：

有三种情况需要处理：(父结点y，左子结点x，孙结点w，请参考“二叉搜索树的旋转”)

(1) 左结点平衡因子为1，即LL形式，直接一次右旋就可以了，注意此时结点y、x平衡因子均为0

(2) 左结点平衡因子为-1，即LR形式，先左旋，将结点w转上去，然后再右旋，使得w取代y成为当前子树的根结点，这时需要根据原有w的平衡因子来更新y x w的平衡因子

(3) 左结点平衡因子为0，只要有删除时才会出现这种情况，直接右旋，然后更新平衡因子

AVL 树的插入

void avl_insert(struct avl_node *node, struct avl_root *root)
{
    struct avl_node *p = root->avl_node, *parent = NULL;

    /* find which position to be inserted and find the first un balance */
    while (p) {
        parent = p;
        if (node->key < p->key)
            p = p->left;
        else
            p = p->right;
    }

    node->parent = parent;
    if (parent == NULL) {
        root->avl_node = node;
    }
    else {
        if (node->key < parent->key)
            parent->left = node;
        else 
            parent->right = node;
    }

    /* adjust balance factor, may be using rotations */
    for (p = node;parent;) {
        if (parent->left == p)
            parent->factor++;
        else 
            parent->factor--;
        
        if (parent->factor == 0)
            break;
        else if (parent->factor == -2 || parent->factor == 2) {
            avl_balance(parent, root);
            break;
        }
        p = parent;
        parent = parent->parent;
    }
}

AVL 插入时，首先类似BST的插入，然后从插入结点往上回溯，更新祖先结点的平衡因子，如果某祖先的平衡因子更新后为0，说明从此结点往上平衡因子均不需要改变，则调整结束。否则找到第一个不平衡结点对其调整，当这个结点调整完后，AVL树必定重新平衡，可以看到AVL 树的插入最多需要一次平衡调整，最多两次旋转

AVL 树的删除

static void avl_del_balance(int dir, struct avl_node *parent, struct avl_root *root)
{
    struct avl_node *node;

    if (dir == 1) {
        parent->factor++;
        if (parent->factor == 2)
            parent = avl_balance(parent, root);
    }
    else {
        parent->factor--;
        if (parent->factor == -2)
            parent = avl_balance(parent, root);
    }
    if (parent->factor != 0)
        return;
    node = parent;
    parent = parent->parent;
        
    while (parent) {
        if (parent->right == node) {
            parent->factor++;
            if (parent->factor == 2) 
                parent = avl_balance(parent, root);
        }
        else {
            parent->factor--;
            if (parent->factor == -2)
                parent = avl_balance(parent, root);
        }
        if (parent->factor != 0)
            break;
        node = parent;
        parent = parent->parent;
    }
}


void avl_delete(struct avl_node *node, struct avl_root *root)
{
    int dir = 0;                /* 0 means left, 1 means right */
    struct avl_node *child, *parent;

    if (node->left == NULL)
        child = node->right;
    else if (node->right == NULL)
        child = node->left;
    else {        /* use successor instead of node */
        struct avl_node *old = node, *left;

        node = node->right;
        while ((left = node->left) != NULL)
            node = left;
        child = node->right;
        parent = node->parent;

        if (child)
            child->parent = parent;

        if (old == parent) {/* successor is just the right child of node */
            parent->right = child;
            dir = 1;
            parent = node;
        }
        else
            parent->left = child;

        /* update successor as old node */
        node->parent = old->parent;
        node->factor = old->factor;        
        node->right = old->right;
        node->left = old->left;
        if (old->parent) {
            if (old->parent->left == old)
                old->parent->left = node;
            else
                old->parent->right = node;
        }
        else
            root->avl_node = node;

        old->left->parent = node;
        if (old->right)
            old->right->parent = node;

        goto balance;
    }

    /* only used for node is at most one degree node. */
    parent = node->parent;
    if (child)
        child->parent = parent;
    if (parent) {
        if (parent->left == node)
            parent->left = child;
        else {
            dir = 1;
            parent->right = child;
        }
    }
    else
        root->avl_node = child;

balance:
    if (parent)
        avl_del_balance(dir, parent, root);
}

删除相对复杂，首先是BST的删除，然后再从删除结点的父结点往上回溯并更新平衡因子，如果发现某祖先结点变为不平衡结点，则进行平衡调整。如果某祖先结点的平衡因子不为0，则调整结束，注意删除、插入的平衡调整函数相同，均为avl_balance。可以看到删除最多需要调整logn次，即最多有logn * 2的旋转操作。

在使用随机数进行测试时，AVL 树的删除相比红黑树要慢10%-20%，但其插入操作仅比红黑树慢5%以内