Dijkstra算法与实现--基础篇
一、Dijkstra 算法的介绍
Dijkstra 算法,又叫迪科斯彻算法(Dijkstra),算法解决的是有向图中单个源点到其他顶点的最短路径问题。举例来说,如果图中的顶点表示城市,而边上的权重表示著城市间开车行经的距离,Dijkstra 算法可以用来找到两个城市之间的最短路径。
Floyd-Warshall算法所求的是图中任意两点间的最短距离,时间复杂度为O(n^3),而Dijkstra算法所求的是单源最短路径,一般情况下,其时间复杂度为O(n^2),若矩阵足够稀疏可通过使用binary min-heap使得时间复杂度降为O(n^2/lgn),用斐波那契堆的话,复杂度O(E+NlgN)。总的来说,在权值非负的图中求单源最短路径时,Dijkstra算法是最优选择。
二、图文解析 Dijkstra 算法
Dijkstra算法是典型最短路径算法,用于计算一个节点到其他所有节点的最短路径。不过,针对的是非负值权边。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。[Dijkstra算法能得出最短路径的最优解,但由于它遍历计算的节点很多,所以效率低。]
如下图,设A为源点,求A到其他各所有一一顶点(B、C、D、E、F)的最短路径。线上所标注为相邻线段之间的距离,即权值。
(注:此图为随意所画,其相邻顶点间的距离与图中的目视长度不能一一对等)
Dijkstra无向图
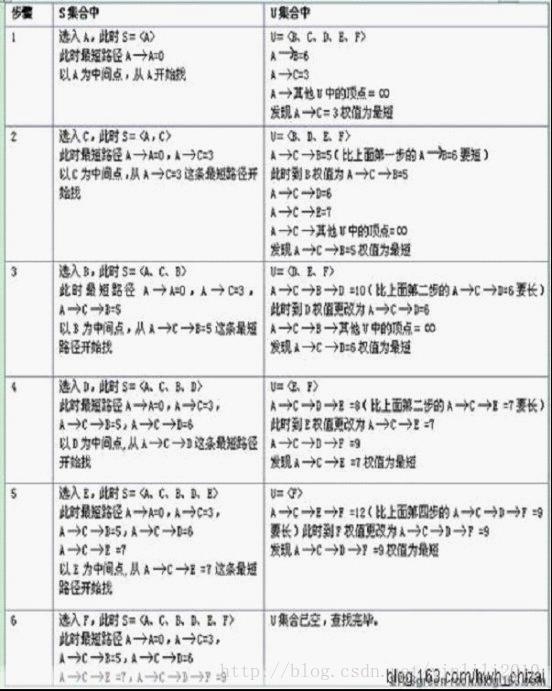
算法执行步骤如下表:
三、深入浅出,彻底解剖Dijkstra 算法
I、松弛技术RELAX的介绍
Dijkstra 算法使用了松弛技术,对每个顶点v<-V,都设置一个属性d[v],用来描述从源点s到v的最短路径上权值的上界,
称为最短路径的估计。
首先,得用O(V)的时间,来对最短路径的估计,和对前驱进行初始化工作。
INITIALIZE-SINGLE-SOURCE(G, s)
1 for each vertex v ∈ V[G]
2 do d[v] ← ∞
3 π[v] ← NIL //O(V)???
4 d[s] 0
RELAX(u, v, w)
1 if d[v] > d[u] + w(u, v)
2 then d[v] ← d[u] + w(u, v)
3 π[v] ← u //O(E)
图。
II、Dijkstra 算法
此Dijkstra 算法分三个步骤,
INSERT (第3行), EXTRACT-MIN (第5行), 和DECREASE-KEY(第8行的RELAX,调用此减小关键字的操作)。
DIJKSTRA(G, w, s)
1 INITIALIZE-SINGLE-SOURCE(G, s) //对每个顶点初始化 ,O(V)
2 S ← Ø
3 Q ← V[G] //INSERT,O(1), Q= 图中的U集合
4 while Q ≠ Ø
5 do u ← EXTRACT-MIN(Q) //简单的O(V*V);二叉/项堆,和FIB-HEAP的话,则都为O(V*lgV)。
6 S ← S ∪{u}
7 for each vertex v ∈ Adj[u]
8 do RELAX(u, v, w) //简单方式:O(E),二叉/项堆,E*O(lgV),FIB-HEAP,E*O(1)。
其中Q集合记录所有没有固定过的点,第五行表示在Q中找出离原点最近的点u作为下一个固定点,然后,通过u所延伸的路径更新原点与其他点的距离。
四、简单的Dijkstra算法的实现
使用C++实现例子所示的无向图,其中vector<bool> isInS, 如果0节点在S中,则isInS[0] = true, 所以找S中的数需要从0到num找出为真的, 找Q中的需要从0到num找出值为假的。实现的代码如下:
#include <iostream>
#include <iostream>
#include <vector>
#include <stack>
using namespace std;
int map[][6] = { //定义无向图,或者有向图
{0, 6, 3, INT_MAX, INT_MAX, INT_MAX},
{6, 0, 2, 5,INT_MAX, INT_MAX},
{3, 2, 0, 3,4, INT_MAX},
{INT_MAX,5, 3, 0, 2, 3},
{INT_MAX,INT_MAX, 4, 2, 0, 5},
{INT_MAX,INT_MAX,INT_MAX,3,5,0}
};
void Dijkstra(
const int numOfVertex, /*节点数目*/
const int startVertex, /*源节点*/
int (map)[][6], /*有向图邻接矩阵*/
int *distance, /*各个节点到达源节点的距离*/
int *prevVertex /*各个节点的前一个节点*/
)
{
vector<bool> isInS; //是否已经在S集合中
isInS.reserve(0);
isInS.assign(numOfVertex, false); //初始化,所有的节点都不在S集合中 , 分配numOfVertex个字节
//step1
/*初始化distance和prevVertex数组*/
for(int i =0; i < numOfVertex; ++i)
{
distance[ i ] = map[ startVertex ][ i ]; //源节点到各个节点的距离,其中INT_MAX代表不可达
if(map[ startVertex ][ i ] < INT_MAX) //如果是可达的
prevVertex[ i ] = startVertex;
else
prevVertex[ i ] = -1; //表示还不知道前一个节点是什么
}
prevVertex[ startVertex ] = -1; //源节点无前一个节点
/*开始使用贪心思想循环处理不在S集合中的每一个节点*/
isInS[startVertex] = true; //开始节点放入S集合中
int currentVertex = startVertex;
for (int i = 1; i < numOfVertex; i ++) //这里循环从1开始是因为开始节点已经存放在S中了,还有numOfVertex-1个节点要处理
{
//step2
/*在Q中选择u到j的distance最小的一个节点, 如第一步A到C,最后目标到D*/
int minDistance = INT_MAX;
for(int j = 0; j < numOfVertex; ++j) //
{
if((isInS[j] == false) && (distance[j] < minDistance))//寻找初始currentVertexA到Q中distance最小的节点 最后为新的currentVertexC
{
currentVertex = j;
minDistance = distance[j];
}
}
isInS[currentVertex] = true;//将这个节点currentVertex放入S集合中
//step3
/*对这个新的currentVertexC做松弛计算,更新distance*/
for (int j =0; j < numOfVertex; j ++)
{
if (isInS[j] == false && map[currentVertex][j] < INT_MAX) //在Q中,有距离的为c->d,c->e, c->b
{
int currentdist = distance[ currentVertex] + map[ currentVertex ][ j ];
if (currentdist < distance[ j ]) //distance[j]为开始到j的距离
{
distance[ j ] = currentdist;
prevVertex[ j ] = currentVertex;
}
}
}
}
}
int main (int argc, const char * argv[])
{
int distance[6];
int preVertex[6];
//for (int i =0 ; i < 5; ++i ) //源目标为i的
//{
Dijkstra(6, 0, map, distance, preVertex);
//for(int j =0; j < 6; ++j)
//{
int index = 5; //加上for目标为j的
stack<int > trace;
while (preVertex[index] != -1) {
trace.push(preVertex[index]);
cout<<"push"<<preVertex[index]<<endl;
index = preVertex[index];
}
cout << "路径:";
while (!trace.empty()) {
cout<<trace.top()<<" -- ";
trace.pop();
}
cout <<5; //j
cout <<" 距离是:"<<distance[5]<<endl; //j
// }
//}
system("pause");
return 0;
}
上面的代码可以看出要得到源A到F的路径,需要搜索整个图, 而不是一部分,如果最后的打印加上For,是可以得到源到其他点的最短路径的。
distance[j]记录当源节点到当前节点j当前的最短距离。在算法中不断的更新到最优值。
不能对单个目标节点求最短路径,因为她是需要一步一步更新到目标节点的操作,