KPM、BM、 AC、ACBM算法分析
说明：本文章有从参考其它文章，如有冒犯，请多原谅。
KPM、BM、 AC、ACBM算法分析
目录
- 简介
- KPM算法简介
- BM算法 简介
- AC算法简介
- ACBM算法简介
简介
最近在定位DPI应用识别的问题，总是发现在特征数量达到一定规模的时候，特征匹配不出来;所以又得投身于分析有点难搞的ACBM算法了。不过最终确定该问题并不是匹配部分问题，而是初始化编译状态机的问题。
在分析该问题过程中，ACBM算法的有些细节的原理忘记了，看起代码来有点吃力；没办法只能搜索各种资料了，在这把自己搜索到的相关资料整理一下，希望对大家有点帮助。
KPM算法
在分析KPM算法之前，先看一下我们最容易想到的查找办法。
首先，字符串”BBC ABCDAB ABCDABCDABDE”的第一个字符与搜索词”ABCDABD”的第一个字符，进行比较。因为B与A不匹配，所以搜索词后移一位。
因为B与A不匹配，搜索词再往后移这里写图片描述
就这样，直到字符串有一个字符，与搜索词的第一个字符相同为止
接着比较字符串和搜索词的下一个字符，还是相同。
直到字符串有一个字符，与搜索词对应的字符不相同为止。
这时，最自然的反应是，将搜索词整个后移一位，再从头逐个比较。这样做虽然可行，但是效率很差，因为你要把”搜索位置”移到已经比较过的位置，重比一遍。
一个基本事实是，当空格与D不匹配时，你其实知道前面六个字符是”ABCDAB”。KMP算法的想法是，设法利用这个已知信息，不要把”搜索位置”移回已经比较过的位置，继续把它向后移，这样就提高了效率。
怎么做到这一点呢？可以针对搜索词，算出一张《部分匹配表》（Partial Match Table）。这张表是如何产生的，后面再介绍，这里只要会用就可以了。后面会详细分析部分匹配值的计算方法。
已知空格与D不匹配时，前面六个字符”ABCDAB”是匹配的。查表可知，最后一个匹配字符B对应的”部分匹配值”为2，因此按照下面的公式算出向后移动的位数：
移动位数 = 已匹配的字符数 - 对应的部分匹配值
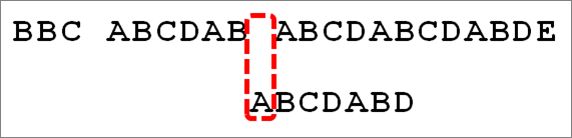
因为 6 - 2 等于4，所以将搜索词向后移动4位。移动4位后结果如下图
因为空格与Ｃ不匹配，搜索词还要继续往后移。这时，已匹配的字符数为2（”AB”），对应的”部分匹配值”为0。所以，移动位数 = 2 - 0，结果为 2，于是将搜索词向后移2位。
因为空格与A不匹配，继续后移一位
逐位比较，直到发现C与D不匹配。于是，移动位数 = 6 - 2，继续将搜索词向后移动4位
逐位比较，直到搜索词的最后一位，发现完全匹配，于是搜索完成。如果还要继续搜索（即找出全部匹配），移动位数 = 7 - 0，再将搜索词向后移动7位。
部分匹配值表计算方法
“部分匹配值”就是”前缀”和”后缀”的最长的共有元素的长度。以”ABCDABD”为例，
－ “A”的前缀和后缀都为空集，共有元素的长度为0；
－ “AB”的前缀为[A]，后缀为[B]，共有元素的长度为0；
－ “ABC”的前缀为[A, AB]，后缀为[BC, C]，共有元素的长度0；
－ “ABCD”的前缀为[A, AB, ABC]，后缀为[BCD, CD, D]，共有元素的长度为0；
－ “ABCDA”的前缀为[A, AB, ABC, ABCD]，后缀为[BCDA, CDA, DA, A]，共有元素为”A”，长度为1；
－ “ABCDAB”的前缀为[A, AB, ABC, ABCD, ABCDA]，后缀为[BCDAB, CDAB, DAB, AB, B]，共有元素为”AB”，长度为2；
－ “ABCDABD”的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB]，后缀为[BCDABD, CDABD, DABD, ABD, BD, D]，共有元素的长度为0。
计算特征串next值得c语言代码
void getNext(const char *p,int next[])//多算一位的next算法
{
int j=-1,i=0;
next[0]=-1;
int len=strlen(p);
while(i<=len)
{
if(j==-1||p[i]==p[j])
{
i++;
j++;
//next[i]=j;//以下是改进的算法
if(p[i]!=p[j]) next[i]=j;
else next[i]=next[j];
}
else j=next[j];
}
}
待续，BM、ACBM算法下次继续