卡特兰数总结

中间部分，小部分内容摘自百度百科
结尾部分，小部分内容摘自http://blog.sina.com.cn/u/1885661061

卡特兰数是组合数学中一个常出现在各种计数问题中出现的数列。这是一个很神奇的数列，就像黄金分割点在大自然中被神奇的应用。组合数学中也有很多问题是关于卡特兰数的。

卡特兰数的前几项是1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786,……..如果你发现测试数据里有这些数字，就表明，哎，这道题目可能是特斯拉数的应用。

卡特兰数的递推式：h(n)= h(0)*h(n-1)+h(1)*h(n-2) + … + h(n-1)h(0) (n>=2)
通项公式：h(n)=h(n-1)*(4*n-2)/(n+1);
递推式是怎么得来的，其实下面的应用中都可以证明。

第一个应用：
括号的匹配：给你2*n个括号，当然是n个左括号，n个右括号，这样才能匹配。问有多少种匹配方式，假设n=2，只有()()，(())两种。这个问题的答案就是特斯拉数，这里的理论证明放到第二个应用里说。
我当然可以用动态规划来解决这个问题，可以验证最终动态规划数组表示的就是卡特兰数。
首先我们把左括号当做1，右括号当作-1.我们设定dp[i][j]表示前i个括号，前缀和为j的数量。所以当前缀和为0时就是我们要求的解。状态转移方程很容易理解，dp[i][j]=dp[i-1][j+1]+dp[i-1][j-1],第i个是左括号自然加1，是右括号自然减1。

      memset(dp,0,sizeof(dp));
      dp[0][0]=1;
      for(int i=1;i<=2*n;i++)
      {
          for(int j=0;j<=n;j++)
          {
               if(j+1<=n) dp[i][j]=(dp[i][j]+dp[i-1][j+1];
               if(j-1>=0) dp[i][j]=(dp[i][j]+dp[i-1][j-1];
          }
      }

这里只有n个左括号，所以j最多有n。打印dp[2*n][0]发现dp[2*n][0]=h(n);

第二个应用：
出栈的次序：给你n个数，进栈的序列是1,2,3,4,…..n，有多少个不同的出栈次序。f(n)表示个数为n的序列的出栈次序种数，这里我们假定最后出栈的元素是k，在k入栈之前比k小值都出栈，所以有f(k-1)种，之后比k大的数在k之前出栈，所以有f(n-k)种，由于比k小和比k大的值入出栈是独立，所以可以用乘法原则，这里很重要，记住卡特兰数是组合数学的数列所以离不开乘法原理和加法原理，在一些应用中也要用到乘法原则，即f(n)=f(k-1)*f(n-k).由于k可以取1到n，根据加法原则，将k取不同的相加可以得到序列总数：f（n）=f（0）f（n-1）+f（1）f（n-2）+……+f（n-1）f（0）。你会发现和一开始的递推式是一样的。
这里把第一个应用，证明一下。因为第一个应用和第二个实际上一回事。

这是放在栈里的一组括号匹配，左括号就相当于n个进栈的数，那左括号什么时候出栈呢？就是当遇到右括号就出栈，右括号没有任何进栈出栈的操作，只是表示其相应的左括号什么时候出栈。所以2*n个括号匹配序列的种数，就相当于n个数出栈次序的种数。

这里给一道题目的连接，就是这个应用的解法。
http://acm.fzu.edu.cn/problem.php?pid=2098
这道题目改进了一下，限制了栈的高度m，否则就是卡特兰数的模板题了。
关于这道题目的解法，除了转换成括号匹配问题（那么前缀和最大就是m）。其实这也是一个简单的动态规划问题。dp[i][j]表示第i个数入栈，栈里还剩的元素。那么第i-1个数，栈里的元素可以是j-1（不出栈）也可以是比j大的数（出栈）。
状态转移方程：dp[i][j]=sum{dp[i-1][m….j-1]};
给出一篇题解博客吧
http://blog.csdn.net/dacc123/article/details/50922580

第三个应用：
给定节点组成二叉树：给定n个点，能构成多少种不同的二叉树。

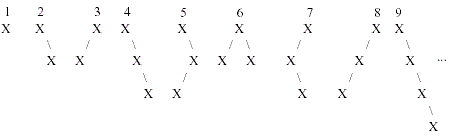
答案是h(n)种。证明很简单，一个二叉树由三部分组成根节点，左子树，右子树。左子树的节点个数可能是0,1,2,3,…n-1,相应的右子树的节点个数可能是n-1,n-2,n-3,……3,2,1,0.由于左子树和右子树是独立的，所以满足乘法原则。根据左子树的不同的节点数会产生不同的情况，满足加法原则所以f（n）=f（0）f（n-1）+f（1）f（n-2）+……+f（n-1）f（0）和一开始的递推式一样。

这里给一道关于这个应用的题目
http://acm.fzu.edu.cn/problem.php?pid=1064
这道理在这个理论上升级了，对二叉树进行排序，给你序数，让你输出这个二叉树。方法是递推，根据这颗树的排名，可以确定左子树的节点个数和右子树的节点个数。给一篇题解博客吧
http://blog.csdn.net/Dacc123/article/details/50922482

第四个应用：
凸包三角形划分：一个凸多边形种，通过若干条互不相交的对角线，把这个凸包划分成若干个三角形，求不同的划分的方案数。

答案就是h(n).
证明：在凸多边形上任意选一个顶点k，并选取任意两个不属于k的两个顶点，构成一个三角形。这个三角形把凸边形分成两个凸边形，由于两边的凸变形相互独立满足乘法原则，又由于k可以取1到n满足加法原则所以：f（n）=f（0）f（n-1）+f（1）f（n-2）+……+f（n-1）f（0）。

给一道题目关于凸包的应用，
http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=3537
这道题目虽然和卡特兰数无关，但是卡特兰数的思想，即把凸包切割成两个凸包，和最优三角划分的思想是一样的。关于凸包还有很多知识，比如凸包算法，给你一些列点，让你输出构成凸包的点。

其他应用：
在n*n的格子中，从左下角走到右上角，不能穿过对角线。只能向右或向上走

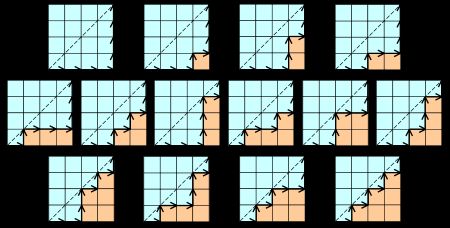
其实向右走相当于进栈，向左走相当于出栈，本质就是n个数出栈次序的问题

在圆上选择2*n个点，将这些点连接起来，所得到n条线段不相交

和凸包切割一个原理

用n个长方形填充一个高度为n的阶梯状图形的方法数

有n+1个叶子的满二叉树的个数

以上的问题答案都是卡特兰数，可见卡特兰数是多么的神奇。